structuralBoundaryLoad
Specify boundary loads for structural model
Domain-specific structural workflow is not recommended. New features might not be compatible with this workflow. For help migrating your existing code to the unified finite element workflow, see Migration from Domain-Specific to Unified Workflow.
Syntax
Description
structuralBoundaryLoad(
specifies the surface traction, pressure, and translational stiffness on the
boundary of type structuralmodel,RegionType,RegionID,"SurfaceTraction",STval,"Pressure",Pval,"TranslationalStiffness",TSval)RegionType with
RegionID ID numbers.
Surface traction is determined as distributed normal and tangential forces acting on a boundary, resolved along the global Cartesian coordinate system.
Pressure must be specified in the direction that is normal to the boundary. A positive pressure value acts into the boundary (for example, compression). A negative pressure value acts away from the boundary (for example, suction).
Translational stiffness is a distributed spring stiffness for each translational direction. Translational stiffness is used to model an elastic foundation.
structuralBoundaryLoad does not require you to specify
all three boundary loads. Depending on your structural analysis problem, you can
specify one or more boundary loads by picking the corresponding arguments and
omitting others. You can specify translational stiffness for any structural
model. To specify pressure or surface traction,
structuralmodel must be a static, transient, or
frequency response model. Structural models for modal analysis cannot have
pressure or surface traction.
The default boundary load is a stress-free boundary condition.
structuralBoundaryLoad(
specifies concentrated force at a vertex with the structuralmodel,"Vertex",VertexID,"Force",Fval)VertexID
number. You can specify force only if structuralmodel is a
static, transient, or frequency response model. Structural models for modal
analysis cannot have concentrated force.
structuralBoundaryLoad(___,"Vectorized","on")
uses vectorized function evaluation when you pass a function handle as an
argument. If your function handle computes in a vectorized fashion, then using
this argument saves time. See Vectorization. For details on this
evaluation, see Nonconstant Boundary Conditions.
Use this syntax with any of the input arguments from previous syntaxes.
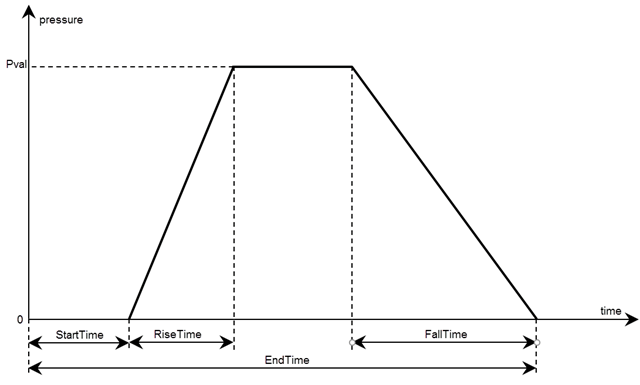
structuralBoundaryLoad(___,"Pressure",
lets you specify the form and duration of a nonconstant pressure pulse and
harmonic excitation for a transient structural model without creating a function
handle. When using this syntax, you must specify the model, region type and
region ID, and pressure. Surface traction and translational stiffness are
optional arguments. This syntax does not work for static, modal analysis, and
frequency response models.Pval,Name,Value)
structuralBoundaryLoad(
lets you specify the form and duration of a nonconstant concentrated force and
harmonic excitation for a transient structural model without creating a function
handle.structuralmodel,"Vertex",VertexID,"Force",Fval,Name,Value)
structuralBoundaryLoad(___,"Label",
adds a label for the structural boundary load to be used by the labeltext)linearizeInput function. This function lets you pass boundary
loads to the linearize function that extracts sparse linear models for use
with Control System Toolbox™.
boundaryLoad = structuralBoundaryLoad(___)
Examples
Apply Fixed Boundaries and Specify Surface Traction
Apply fixed boundaries and traction on two ends of a bimetallic cable.
Create a structural model.
structuralModel = createpde("structural","static-solid");
Create nested cylinders to model a bimetallic cable.
gm = multicylinder([0.01,0.015],0.05);
Assign the geometry to the structural model and plot the geometry.
structuralModel.Geometry = gm; pdegplot(structuralModel,"CellLabels","on", ... "FaceLabels","on", ... "FaceAlpha",0.4)
For each metal, specify Young's modulus and Poisson's ratio.
structuralProperties(structuralModel,"Cell",1,"YoungsModulus",110E9, ... "PoissonsRatio",0.28); structuralProperties(structuralModel,"Cell",2,"YoungsModulus",210E9, ... "PoissonsRatio",0.3);
Specify that faces 1 and 4 are fixed boundaries.
structuralBC(structuralModel,"Face",[1,4],"Constraint","fixed")
ans =
StructuralBC with properties:
RegionType: 'Face'
RegionID: [1 4]
Vectorized: 'off'
Boundary Constraints and Enforced Displacements
Displacement: []
XDisplacement: []
YDisplacement: []
ZDisplacement: []
Constraint: "fixed"
Radius: []
Reference: []
Label: []
Boundary Loads
Force: []
SurfaceTraction: []
Pressure: []
TranslationalStiffness: []
Label: []
Specify the surface traction for faces 2 and 5.
structuralBoundaryLoad(structuralModel, ... "Face",[2,5], ... "SurfaceTraction",[0;0;100])
ans =
StructuralBC with properties:
RegionType: 'Face'
RegionID: [2 5]
Vectorized: 'off'
Boundary Constraints and Enforced Displacements
Displacement: []
XDisplacement: []
YDisplacement: []
ZDisplacement: []
Constraint: []
Radius: []
Reference: []
Label: []
Boundary Loads
Force: []
SurfaceTraction: [3x1 double]
Pressure: []
TranslationalStiffness: []
Label: []
Specify Translational Stiffness
Create a structural model.
structuralModel = createpde("structural","static-solid");
Create a block geometry.
gm = multicuboid(20,10,5);
Assign the geometry to the structural model and plot the geometry.
structuralModel.Geometry = gm; pdegplot(structuralModel,"FaceLabels","on","FaceAlpha",0.5)
Specify Young's modulus and Poisson's ratio.
structuralProperties(structuralModel,"YoungsModulus",30, ... "PoissonsRatio",0.3);
The bottom face of the block rests on an elastic foundation (a spring). To model this foundation, specify the translational stiffness.
structuralBoundaryLoad(structuralModel, ... "Face",1, ... "TranslationalStiffness",[0;0;30])
ans =
StructuralBC with properties:
RegionType: 'Face'
RegionID: 1
Vectorized: 'off'
Boundary Constraints and Enforced Displacements
Displacement: []
XDisplacement: []
YDisplacement: []
ZDisplacement: []
Constraint: []
Radius: []
Reference: []
Label: []
Boundary Loads
Force: []
SurfaceTraction: []
Pressure: []
TranslationalStiffness: [3x1 double]
Label: []
Apply Concentrated Force at Point
Specify a force value at a vertex of a geometry.
Create a structural model for static analysis of a solid (3-D) problem.
model = createpde("structural","static-solid");
Create the geometry, which consists of two cuboids stacked on top of each other.
gm = multicuboid(0.2,0.01,[0.01 0.01],"Zoffset",[0 0.01]);Include the geometry in the structural model.
model.Geometry = gm;
Plot the geometry and display the face labels. Rotate the geometry so that you can see the face labels on the left side.
figure pdegplot(model,"FaceLabels","on"); view([-67 5])
Plot the geometry and display the vertex labels. Rotate the geometry so that you can see the vertex labels on the right side.
figure pdegplot(model,"VertexLabels","on","FaceAlpha",0.5) xlim([-0.01 0.1]) zlim([-0.01 0.02]) view([60 5])
Specify Young's modulus, Poisson's ratio, and the mass density of the material.
structuralProperties(model,"YoungsModulus",201E9,"PoissonsRatio",0.3);
Specify that faces 5 and 10 are fixed boundaries.
structuralBC(model,"Face",[5 10],"Constraint","fixed");
Specify the concentrated force at vertex 6.
structuralBoundaryLoad(model,"Vertex",6,"Force",[0;10^4;0])
ans =
StructuralBC with properties:
RegionType: 'Vertex'
RegionID: 6
Vectorized: 'off'
Boundary Constraints and Enforced Displacements
Displacement: []
XDisplacement: []
YDisplacement: []
ZDisplacement: []
Constraint: []
Radius: []
Reference: []
Label: []
Boundary Loads
Force: [3x1 double]
SurfaceTraction: []
Pressure: []
TranslationalStiffness: []
Label: []
Specify Pressure for Frequency Response Model
Use a function handle to specify a frequency-dependent pressure for a frequency response model.
Create a frequency response model for a 3-D problem.
fmodel = createpde("structural","frequency-solid");
Import and plot the geometry.
importGeometry(fmodel,"TuningFork.stl"); figure pdegplot(fmodel,"FaceLabels","on")
Specify the pressure loading on a tine (face 11) as a short rectangular pressure pulse. In the frequency domain, this pressure pulse is a unit load uniformly distributed across all frequencies.
structuralBoundaryLoad(fmodel,"Face",11,"Pressure",1);
Now specify a frequency-dependent pressure load, for example, .
pLoad = @(location,state) exp(-(state.frequency-1E3).^2/1E5); structuralBoundaryLoad(fmodel,"Face",12,"Pressure",pLoad);
Specify Nonconstant Pressure For Transient Model by Using Function Handle
Use a function handle to specify a harmonically varying pressure at the center of a thin 3-D plate.
Create a transient dynamic model for a 3-D problem.
structuralmodel = createpde("structural","transient-solid");
Create a geometry consisting of a thin 3-D plate with a small plate at the center. Include the geometry in the model and plot it.
gm = multicuboid([5,0.05],[5,0.05],0.01); structuralmodel.Geometry = gm; pdegplot(structuralmodel,"FaceLabels","on","FaceAlpha",0.5)
Zoom in to see the face labels on the small plate at the center.
figure pdegplot(structuralmodel,"FaceLabels","on","FaceAlpha",0.25) axis([-0.2 0.2 -0.2 0.2 -0.1 0.1])
Specify Young's modulus, Poisson's ratio, and the mass density of the material.
structuralProperties(structuralmodel,"YoungsModulus",210E9,... "PoissonsRatio",0.3,... "MassDensity",7800);
Specify that all faces on the periphery of the thin 3-D plate are fixed boundaries.
structuralBC(structuralmodel,"Constraint","fixed","Face",5:8);
Apply a harmonically varying pressure load on the small face at the center of the plate.
plungerLoad = @(location,state)5E7.*sin(25.*state.time); structuralBoundaryLoad(structuralmodel,"Face",12,"Pressure",plungerLoad)
ans =
StructuralBC with properties:
RegionType: 'Face'
RegionID: 12
Vectorized: 'off'
Boundary Constraints and Enforced Displacements
Displacement: []
XDisplacement: []
YDisplacement: []
ZDisplacement: []
Constraint: []
Radius: []
Reference: []
Label: []
Boundary Loads
Force: []
SurfaceTraction: []
Pressure: @(location,state)5E7.*sin(25.*state.time)
TranslationalStiffness: []
Label: []
Time Variation of Force, Pressure, or Enforced Displacement
StartTime: []
EndTime: []
RiseTime: []
FallTime: []
Sinusoidal Variation of Force, Pressure, or Enforced Displacement
Frequency: []
Phase: []
Apply Sinusoidal Pressure by Specifying Frequency
Specify a harmonically varying pressure at the center of a thin 3-D plate by specifying its frequency.
Create a transient dynamic model for a 3-D problem.
structuralmodel = createpde("structural","transient-solid");
Create a geometry consisting of a thin 3-D plate with a small plate at the center. Include the geometry in the model and plot it.
gm = multicuboid([5,0.05],[5,0.05],0.01); structuralmodel.Geometry=gm; pdegplot(structuralmodel,"FaceLabels","on","FaceAlpha",0.5)
Zoom in to see the face labels on the small plate at the center.
figure pdegplot(structuralmodel,"FaceLabels","on","FaceAlpha",0.25) axis([-0.2 0.2 -0.2 0.2 -0.1 0.1])
Specify Young's modulus, Poisson's ratio, and the mass density of the material.
structuralProperties(structuralmodel,"YoungsModulus",210E9,... "PoissonsRatio",0.3,... "MassDensity",7800);
Specify that all faces on the periphery of the thin 3-D plate are fixed boundaries.
structuralBC(structuralmodel,"Constraint","fixed","Face",5:8);
Apply a harmonically varying pressure load on the small face at the center of the plate.
structuralBoundaryLoad(structuralmodel,"Face",12, ... "Pressure",5E7, ... "Frequency",25)
ans =
StructuralBC with properties:
RegionType: 'Face'
RegionID: 12
Vectorized: 'off'
Boundary Constraints and Enforced Displacements
Displacement: []
XDisplacement: []
YDisplacement: []
ZDisplacement: []
Constraint: []
Radius: []
Reference: []
Label: []
Boundary Loads
Force: []
SurfaceTraction: []
Pressure: 50000000
TranslationalStiffness: []
Label: []
Time Variation of Force, Pressure, or Enforced Displacement
StartTime: []
EndTime: []
RiseTime: []
FallTime: []
Sinusoidal Variation of Force, Pressure, or Enforced Displacement
Frequency: 25
Phase: []
Apply Rectangular Pressure Pulse on Boundary
Create a transient structural model.
structuralModel = createpde("structural","transient-solid");
Import and plot the geometry.
importGeometry(structuralModel,"BracketWithHole.stl"); pdegplot(structuralModel,"FaceLabels","on") view(-20,10)
Specify Young's modulus and Poisson's ratio.
structuralProperties(structuralModel,"YoungsModulus",200e9, ... "PoissonsRatio",0.3,... "MassDensity",7800);
Specify that face 4 is a fixed boundary.
structuralBC(structuralModel,"Face",4,"Constraint","fixed");
Apply a rectangular pressure pulse on face 7 in the direction normal to the face.
structuralBoundaryLoad(structuralModel,"Face",7,"Pressure",10^5,... "StartTime",0.1,"EndTime",0.5)
ans =
StructuralBC with properties:
RegionType: 'Face'
RegionID: 7
Vectorized: 'off'
Boundary Constraints and Enforced Displacements
Displacement: []
XDisplacement: []
YDisplacement: []
ZDisplacement: []
Constraint: []
Radius: []
Reference: []
Label: []
Boundary Loads
Force: []
SurfaceTraction: []
Pressure: 100000
TranslationalStiffness: []
Label: []
Time Variation of Force, Pressure, or Enforced Displacement
StartTime: 0.1000
EndTime: 0.5000
RiseTime: []
FallTime: []
Sinusoidal Variation of Force, Pressure, or Enforced Displacement
Frequency: []
Phase: []
Apply Rectangular Force Pulse at Point
Specify a short concentrated force pulse at a vertex of a geometry.
Create a structural model for static analysis of a solid (3-D) problem.
structuralmodel = createpde("structural","transient-solid");
Create the geometry, which consists of two cuboids stacked on top of each other.
gm = multicuboid(0.2,0.01,[0.01 0.01],"Zoffset",[0 0.01]);Include the geometry in the structural model.
structuralmodel.Geometry = gm;
Plot the geometry and display the face labels. Rotate the geometry so that you can see the face labels on the left side.
figure pdegplot(structuralmodel,"FaceLabels","on"); view([-67 5])
Plot the geometry and display the vertex labels. Rotate the geometry so that you can see the vertex labels on the right side.
figure pdegplot(structuralmodel,"VertexLabels","on","FaceAlpha",0.5) xlim([-0.01 0.1]) zlim([-0.01 0.02]) view([60 5])
Specify Young's modulus, Poisson's ratio, and the mass density of the material.
structuralProperties(structuralmodel,"YoungsModulus",201E9, ... "PoissonsRatio",0.3, ... "MassDensity",7800);
Specify that faces 5 and 10 are fixed boundaries.
structuralBC(structuralmodel,"Face",[5 10],"Constraint","fixed");
Specify a short concentrated force pulse at vertex 6.
structuralBoundaryLoad(structuralmodel,"Vertex",6, ... "Force",[0;1000;0], ... "StartTime",1, ... "EndTime",1.05)
ans =
StructuralBC with properties:
RegionType: 'Vertex'
RegionID: 6
Vectorized: 'off'
Boundary Constraints and Enforced Displacements
Displacement: []
XDisplacement: []
YDisplacement: []
ZDisplacement: []
Constraint: []
Radius: []
Reference: []
Label: []
Boundary Loads
Force: [3×1 double]
SurfaceTraction: []
Pressure: []
TranslationalStiffness: []
Label: []
Time Variation of Force, Pressure, or Enforced Displacement
StartTime: 1
EndTime: 1.0500
RiseTime: []
FallTime: []
Sinusoidal Variation of Force, Pressure, or Enforced Displacement
Frequency: []
Phase: []
Specify zero initial displacement and velocity.
structuralIC(structuralmodel,"Displacement",[0;0;0],"Velocity",[0;0;0])
ans =
GeometricStructuralICs with properties:
RegionType: 'Cell'
RegionID: [1 2]
InitialDisplacement: [3×1 double]
InitialVelocity: [3×1 double]
Generate a fine mesh.
generateMesh(structuralmodel,"Hmax",0.02);Because the load is zero for the initial time span and is applied for only a short time, solve the model for two time spans. Use the first time span to find the solution before the force pulse.
structuralresults1 = solve(structuralmodel,0:1E-2:1);
Use the second time span to find the solution during and after the force pulse.
structuralIC(structuralmodel,structuralresults1)
ans =
NodalStructuralICs with properties:
InitialDisplacement: [1543×3 double]
InitialVelocity: [1543×3 double]
structuralresults2 = solve(structuralmodel, ...
[1.001:0.001:1.01 1.02:1E-2:2]);Plot the displacement value at the node corresponding to vertex 6, where you applied the concentrated force pulse.
loadedNd = findNodes(structuralmodel.Mesh,"region","Vertex",6); plot(structuralresults2.SolutionTimes, ... structuralresults2.Displacement.uy(loadedNd,:))
Input Arguments
structuralmodel — Structural model
StructuralModel object
Structural model, specified as a StructuralModel
object. The model contains the geometry, mesh, structural properties of the
material, body loads, boundary loads, and boundary conditions.
Example: structuralmodel =
createpde("structural","transient-solid")
RegionType — Geometric region type
"Edge" for a 2-D model | "Face" for a 3-D model
Geometric region type, specified as "Edge" for a 2-D
model or "Face" for a 3-D model.
Example: structuralBoundaryLoad(structuralmodel,"Face",[2,5],"SurfaceTraction",[0,0,100])
Data Types: char | string
RegionID — Geometric region ID
positive integer | vector of positive integers
Geometric region ID, specified as a positive integer or vector of positive
integers. Find the region IDs by using pdegplot.
Example: structuralBoundaryLoad(structuralmodel,"Face",[2,5],"SurfaceTraction",[0,0,100])
Data Types: double
VertexID — Vertex ID
positive integer | vector of positive integers
Vertex ID, specified as a positive integer or vector of positive integers.
Find the vertex IDs using pdegplot.
Example: structuralBoundaryLoad(structuralmodel,"Vertex",6,"Force",[0;10^4;0])
Data Types: double
STval — Distributed normal and tangential forces on boundary
numeric vector | function handle
Distributed normal and tangential forces on the boundary, resolved along the global Cartesian coordinate system, specified as a numeric vector or function handle. A numeric vector must contain two elements for a 2-D model and three elements for a 3-D model.
The function must return a two-row matrix for a 2-D model and a three-row
matrix for a 3-D model. Each column of the matrix must correspond to the
surface traction vector at the boundary coordinates provided by the solver.
In case of a transient or frequency response analysis,
STval also can be a function of time or frequency,
respectively. For details, see More About.
Example: structuralBoundaryLoad(structuralmodel,"Face",[2,5],"SurfaceTraction",[0;0;100])
Data Types: double | function_handle
Pval — Pressure normal to boundary
number | function handle
Pressure normal to the boundary, specified as a number or function handle. A positive-value pressure acts into the boundary (for example, compression), while a negative-value pressure acts away from the boundary (for example, suction).
If you specify Pval as a function handle, the function
must return a row vector where each column corresponds to the value of
pressure at the boundary coordinates provided by the solver. In case of a
transient structural model, Pval also can be a function
of time. In case of a frequency response structural model,
Pval can be a function of frequency (when specified
as a function handle) or a constant pressure with the same magnitude for a
broad frequency spectrum. For details, see More About.
Example: structuralBoundaryLoad(structuralmodel,"Face",[2,5],"Pressure",10^5)
Data Types: double | function_handle
TSval — Distributed spring stiffness
numeric vector | function handle
Distributed spring stiffness for each translational direction used to
model elastic foundation, specified as a numeric vector or function handle.
A numeric vector must contain two elements for a 2-D model and three
elements for a 3-D model. The custom function must return a two-row matrix
for a 2-D model and a three-row matrix for a 3-D model. Each column of this
matrix corresponds to the stiffness vector at the boundary coordinates
provided by the solver. In case of a transient or frequency response
analysis, TSval also can be a function of time or
frequency, respectively. For details, see More About.
Example: structuralBoundaryLoad(structuralmodel,"Edge",[2,5],"TranslationalStiffness",[0;5500])
Data Types: double | function_handle
Fval — Concentrated force
numeric vector | function handle
Concentrated force at a vertex, specified as a numeric vector or function handle. Use a function handle to specify concentrated force that depends time or frequency. For details, see More About.
Example: structuralBoundaryLoad(structuralmodel,"Vertex",5,"Force",[0;0;10])
Data Types: double | function_handle
labeltext — Label for structural boundary load
character vector | string
Label for the structural boundary load, specified as a character vector or a string.
Data Types: char | string
Name-Value Arguments
Example: structuralBoundaryLoad(structuralmodel,"Face",[2,5],"Pressure",10^5,"RiseTime",0.5,"FallTime",0.5,"EndTime",3)
Use one or more of the name-value pair arguments to specify the form and duration
of the pressure or concentrated force pulse and harmonic excitation for a transient structural model only. Specify the
pressure or force value using the Pval or
Fval argument, respectively.
You can model rectangular, triangular, and trapezoidal pressure or concentrated force pulses. If the start time is 0, you can omit specifying it.
For a rectangular pulse, specify the start and end times.
For a triangular pulse, specify the start time and any two of the following times: rise time, fall time, and end time. You also can specify all three times, but they must be consistent.
For a trapezoidal pulse, specify all four times.
You can model a harmonic pressure or concentrated force load by specifying its frequency and initial phase. If the initial phase is 0, you can omit specifying it.
Output Arguments
More About
Version History
Introduced in R2017b
You can also select a web site from the following list
Americas
- América Latina (Español)
- Canada (English)
- United States (English)
Europe
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)
Asia Pacific
- Australia (English)
- India (English)
- New Zealand (English)
- 中国
- 日本Japanese (日本語)
- 한국Korean (한국어)