Optimize Live Editor Task with fmincon Solver
This example shows how to use the solver-based Optimize Live Editor task with the
fmincon solver to minimize a quadratic subject to linear
and nonlinear constraints and bounds.
Consider the problem of finding [x1, x2] that solves
subject to the constraints
The starting point x0 for this problem is
x1 = 3 and
x2 = 1.
Start Optimize Live Editor Task
Create a new live Script by clicking the New Live Script button in the File section on the Home tab.

Insert an Optimize Live Editor task. Click the Insert tab and then, in the Code section, select Task > Optimize.


For this example, choose the solver-based task.

For later use in entering problem data, select Insert > Section Break. New sections appear above and below the task.
Enter Problem Data
Starting from the top of the task, enter the problem type and constraint types. Click the Objective > Quadratic button and the Constraints > Lower bounds, Linear inequality, and Nonlinear buttons. The task shows that the recommended solver is
fmincon.Objective Function
The objective function is simple enough to represent as an anonymous function. Position the cursor in the section above the task and enter this code.
fun = @(x)sum(x.^2);
Lower Bound
The problem contains the lower bound x1 ≥ 0.5. Express this bound as a variable
lb. With the cursor at the end of the line defining the objective function, press Enter, and enter the following code to specify the lower bound.lb = [0.5 -Inf];
Initial Point
With the cursor at the end of the line defining the lower bound, press Enter, and enter the following code to set the initial point.
x0 = [3,1];
Linear Constraint
With the cursor at the end of the line defining the initial point, press Enter, and enter the following code to set the linear constraint.
A = [-1,-1]; b = -1;
Run Section
The top section now includes five parameters.
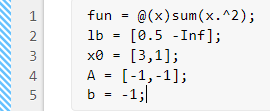
Next, you need to run the section to place the parameters in the workspace as variables. To do so, click the left-most area of the section, which contains a bar of diagonal stripes. After you click this area, the bar becomes a solid bar, indicating the variables are now in the workspace. (Note: You can also press Ctrl+Enter to run the section.)
Set Problem Data
Enter the variables in the Select problem data section of the task. To specify the objective function, select Objective function > Function handle and choose fun.
Set the initial point x0.
Select Lower bounds > From workspace and select lb.
Set the linear inequality constraint variables
Aandbin the Linear inequality area.Now specify the nonlinear inequality constraints. In the Select problem data section, select Nonlinear > Local function, and then click the New button. The function appears in a new section below the task. Edit the resulting code to contain the following uncommented lines.
function [c,ceq] = constraintFcn(x) % You can include commented code lines or not. % Be sure that just these uncommented lines remain: c = [-x(1)^2 - x(2)^2 + 1; -9*x(1)^2 - x(2)^2 + 9; -x(1)^2 + x(2); -x(2)^2 + x(1)]; ceq = []; end
In the Select problem data section, select the constraintFcn function.
Monitor Progress
In the Display progress section of the task, select Text display > Each iteration so you can monitor the solver progress. Select Objective value for the plot.
Your setup looks like this:

Run Solver and Examine Results
To run the solver, click the options button ⁝ at the top right of the task window, and select Run Section.
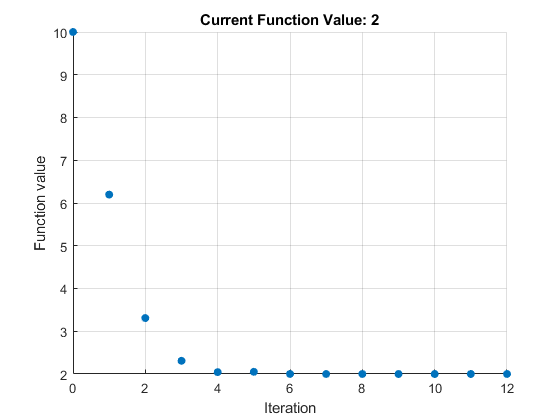
The plot appears in a separate figure window and in the task output area.
To see where the solution variables are returned, look at the top of the task.
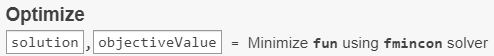
The final point and its associated objective function value appear in the
solution and objectiveValue variables in
the workspace. View these values by entering this code in the live editor section
below the task.
solution, objectiveValue
Press Ctrl+Enter to run the section.
![solution = [1 1], objectiveValue = 2](optimizelet_fmincon_answer.png)