fminsearch Algorithm
fminsearch uses the Nelder-Mead simplex algorithm as described in
Lagarias et al. [57]. This algorithm uses a simplex of n + 1 points for
n-dimensional vectors x. The algorithm first
makes a simplex around the initial guess x0 by
adding 5% of each component
x0(i) to
x0, and using these n
vectors as elements of the simplex in addition to
x0. (The algorithm uses 0.00025 as
component i if x0(i) = 0.) Then, the algorithm modifies the simplex repeatedly according to the
following procedure.
Note
The keywords for the fminsearch iterative
display appear in bold after the
description of the step.
Let x(i) denote the list of points in the current simplex, i = 1,...,n + 1.
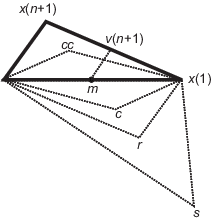
Order the points in the simplex from lowest function value f(x(1)) to highest f(x(n + 1)). At each step in the iteration, the algorithm discards the current worst point x(n + 1), and accepts another point into the simplex. [Or, in the case of step 7 below, it changes all n points with values above f(x(1))].
Generate the reflected point
r = 2m – x(n + 1),
where
m = Σx(i)/n, i = 1...n,
and calculate f(r).
If f(x(1)) ≤ f(r) < f(x(n)), accept r and terminate this iteration. Reflect
If f(r) < f(x(1)), calculate the expansion point s
s = m + 2(m – x(n + 1)),
and calculate f(s).
If f(s) < f(r), accept s and terminate the iteration. Expand
Otherwise, accept r and terminate the iteration. Reflect
If f(r) ≥ f(x(n)), perform a contraction between m and eitherx(n + 1) or r, depending on which has the lower objective function value.
If f(r) < f(x(n + 1)) (that is, r is better than x(n + 1)), calculate
c = m + (r – m)/2
and calculate f(c). If f(c) < f(r), accept c and terminate the iteration. Contract outside
Otherwise, continue with Step 7 (Shrink).
If f(r) ≥ f(x(n + 1)), calculate
cc = m + (x(n + 1) – m)/2
and calculate f(cc). If f(cc) < f(x(n + 1)), accept cc and terminate the iteration. Contract inside
Otherwise, continue with Step 7 (Shrink).
Calculate the n points
v(i) = x(1) + (x(i) – x(1))/2
and calculate f(v(i)), i = 2,...,n + 1. The simplex at the next iteration is x(1), v(2),...,v(n + 1). Shrink
The following figure shows the points that fminsearch might
calculate in the procedure, along with each possible new simplex.
The original simplex has a bold outline. The iterations proceed until
they meet a stopping criterion.