Diese Seite wurde mithilfe maschineller Übersetzung übersetzt. Klicken Sie hier, um die neueste Version auf Englisch zu sehen.

Analyse des Trägheitssensorrauschens mithilfe der Allan-Varianz

Script öffnen

Dieses Beispiel zeigt, wie die Allan-Varianz zur Bestimmung der Rauschparameter eines MEMS-Gyroskops verwendet wird. Diese Parameter können zur Modellierung des Gyroskops in der Simulation verwendet werden. Die Gyroskopmessung wird wie folgt modelliert:

$$\Omega(t) = \Omega_{Ideal}(t) + Bias_N(t) + Bias_B(t) + Bias_K(t)$$

Die drei Rauschparameter N (Winkel-Irrfahrt), K (Raten-Irrfahrt) und B (Bias-Instabilität) werden anhand von Daten geschätzt, die von einem stationären Gyroskop aufgezeichnet wurden.

Hintergrund

Die Allan-Varianz wurde ursprünglich von David W. Allan entwickelt, um die Frequenzstabilität von Präzisionsoszillatoren zu messen. Darüber hinaus können damit auch verschiedene Rauschquellen identifiziert werden, die bei Messungen mit stationären Gyroskopen vorhanden sind. Betrachten Sie L Datenproben von einem Gyroskop mit einer Probenzeit von $\tau_{0}$. Bilden Sie Datencluster mit den Dauern $\tau_{0}$, $2\tau_{0}$, ..., $m\tau_{0}, (m < (L-1)/2)$ und ermitteln Sie die Durchschnittswerte der Summe der in jedem Cluster enthaltenen Datenpunkte über die Länge des Clusters. Die Allan-Varianz wird als Varianz zweier Proben der Datencluster-Durchschnittswerte als Funktion der Cluster-Zeit definiert. In diesem Beispiel wird der überlappende Allan-Varianzschätzer verwendet. Dies bedeutet, dass sich die berechneten Cluster überlappen. Bei größeren Werten von L weist der Schätzer eine bessere Leistung auf als nicht überlappende Schätzer.

Allan Varianzberechnung

Die Allan-Varianz wird wie folgt berechnet:

Loggen Sie L stationäre Gyroskop-Abtastwerte mit einer Abtastperiode von $\tau_{0}$ ein. Lassen Sie $\Omega$ die protokollierten Samples sein.

% Load logged data from one axis of a three-axis gyroscope. This recording
% was done over a six hour period with a 100 Hz sampling rate.
load('LoggedSingleAxisGyroscope', 'omega', 'Fs')
t0 = 1/Fs;

Berechnen Sie für jede Probe den Ausgabewinkel $\theta$:

$$\theta(t) = \int^{t}\Omega(t')dt'$$

Für diskrete Abtastung kann die kumulative Summe multipliziert mit $\tau_{0}$ verwendet werden.

theta = cumsum(omega, 1)*t0;

Berechnen Sie als nächstes die Allan-Varianz:

$$\sigma^2(\tau) =&#10;\frac{1}{2\tau^2}<(\theta_{k+2m}-2\theta_{k+m}+\theta_{k})^2>$$

wobei $\tau = m\tau_{0}$ und $<>$ der Ensemble-Durchschnitt ist.

Der Ensemble-Durchschnitt kann wie folgt erweitert werden:

$$\sigma^2(\tau) =&#10;\frac{1}{2\tau^2(L-2m)}\sum_{k=1}^{L-2m}(\theta_{k+2m} - 2\theta_{k+m}&#10;+ \theta_{k})^2$$

maxNumM = 100;
L = size(theta, 1);
maxM = 2.^floor(log2(L/2));
m = logspace(log10(1), log10(maxM), maxNumM).';
m = ceil(m); % m must be an integer.
m = unique(m); % Remove duplicates.

tau = m*t0;

avar = zeros(numel(m), 1);
for i = 1:numel(m)
    mi = m(i);
    avar(i,:) = sum( ...
        (theta(1+2*mi:L) - 2*theta(1+mi:L-mi) + theta(1:L-2*mi)).^2, 1);
end
avar = avar ./ (2*tau.^2 .* (L - 2*m));

Schließlich wird die Allan-Abweichung $\sigma(t) = \sqrt{\sigma^2(t)}$ verwendet, um die Gyroskop-Rauschparameter zu bestimmen.

adev = sqrt(avar);

figure
loglog(tau, adev)
title('Allan Deviation')
xlabel('\tau');
ylabel('\sigma(\tau)')
grid on
axis equal

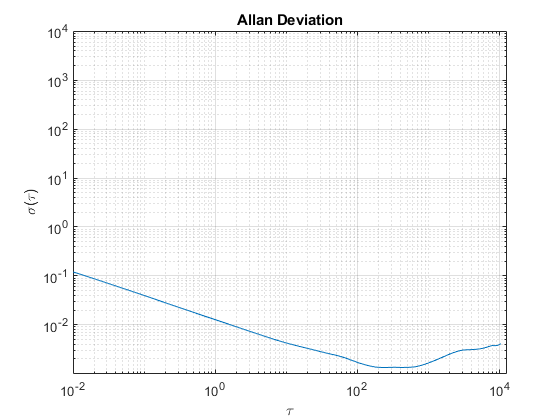
Die Allan-Varianz kann auch mit der Funktion allanvar berechnet werden.

[avarFromFunc, tauFromFunc] = allanvar(omega, m, Fs);
adevFromFunc = sqrt(avarFromFunc);

figure
loglog(tau, adev, tauFromFunc, adevFromFunc);
title('Allan Deviations')
xlabel('\tau')
ylabel('\sigma(\tau)')
legend('Manual Calculation', 'allanvar Function')
grid on
axis equal

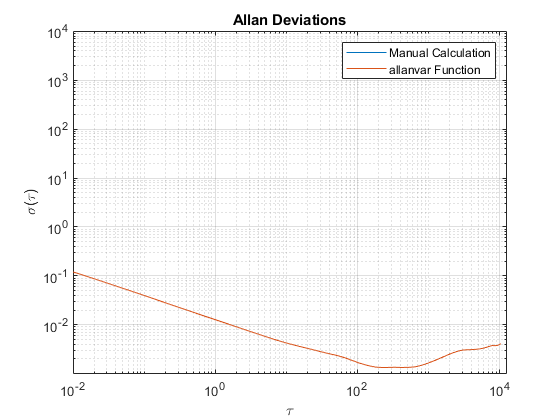
Identifizierung von Rauschparametern

Um die Rauschparameter für das Gyroskop zu erhalten, verwenden Sie die folgende Beziehung zwischen der Allan-Varianz und der zweiseitigen Leistungsspektraldichte (PSD) der Rauschparameter im ursprünglichen Datensatz $\Omega$. Die Beziehung ist:

$$\sigma^2(\tau) = 4\int_{0}^{\infty}S_\Omega(f)&#10;\frac{sin^4(\pi f\tau)}{(\pi f\tau)^2}df$$

Aus der obigen Gleichung geht hervor, dass die Allan-Varianz proportional zur Gesamtrauschleistung des Gyroskops ist, wenn es durch einen Filter mit einer Übertragungsfunktion von $sin^4(x)/(x)^2$ geleitet wird. Diese Übertragungsfunktion ergibt sich aus den Vorgängen, die zum Erstellen und Bedienen der Cluster durchgeführt werden.

Bei dieser Interpretation der Übertragungsfunktion hängt der Filterbandpass von $\tau$ ab. Dies bedeutet, dass unterschiedliche Rauschparameter durch Ändern des Filterbandpasses oder Variieren von $\tau$ identifiziert werden können.

Winkel-Irrfahrt

Die Winkel-Irrfahrt wird durch das weiße Rauschspektrum der Gyroskopausgabe charakterisiert. Die PSD wird vertreten durch:

$$S_\Omega(f) = N^2$$

wobei

N = Winkel-Irrfahrt-Koeffizient

Das Einsetzen in die ursprüngliche PSD-Gleichung und Durchführen einer Integration ergibt:

$$\sigma^2(\tau) = \frac{N^2}{\tau}$$

Die obige Gleichung ist eine Linie mit einer Steigung von -1/2, wenn sie in einem Log-Log-Diagramm von $\sigma(\tau)$ gegenüber $\tau$ aufgetragen wird. Der Wert von N kann direkt aus dieser Zeile bei $\tau = 1$ abgelesen werden. Die Einheiten von N sind $(rad/s)/\sqrt{Hz}$.

% Find the index where the slope of the log-scaled Allan deviation is equal
% to the slope specified.
slope = -0.5;
logtau = log10(tau);
logadev = log10(adev);
dlogadev = diff(logadev) ./ diff(logtau);
[~, i] = min(abs(dlogadev - slope));

% Find the y-intercept of the line.
b = logadev(i) - slope*logtau(i);

% Determine the angle random walk coefficient from the line.
logN = slope*log(1) + b;
N = 10^logN

% Plot the results.
tauN = 1;
lineN = N ./ sqrt(tau);
figure
loglog(tau, adev, tau, lineN, '--', tauN, N, 'o')
title('Allan Deviation with Angle Random Walk')
xlabel('\tau')
ylabel('\sigma(\tau)')
legend('\sigma', '\sigma_N')
text(tauN, N, 'N')
grid on
axis equal

N =

    0.0126

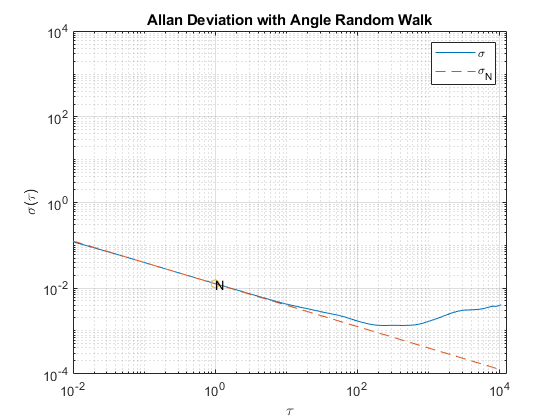
Raten-Irrfahrt

Die Raten-Irrfahrt wird durch das rote Rauschspektrum (Brownsches Rauschen) der Gyroskopausgabe charakterisiert. Die PSD wird vertreten durch:

$$S_\Omega(f) = (\frac{K}{2\pi})^2\frac{1}{f^2}$$

wobei

K = Raten-Irrfahrt-Koeffizient

Das Einsetzen in die ursprüngliche PSD-Gleichung und Durchführen einer Integration ergibt:

$$\sigma^2(\tau) = \frac{K^2\tau}{3}$$

Die obige Gleichung ist eine Linie mit einer Steigung von 1/2, wenn sie in einem Log-Log-Diagramm von $\sigma(\tau)$ gegenüber $\tau$ aufgetragen wird. Der Wert von K kann direkt aus dieser Zeile bei $\tau = 3$ abgelesen werden. Die Einheiten von K sind $(rad/s)\sqrt{Hz}$.

% Find the index where the slope of the log-scaled Allan deviation is equal
% to the slope specified.
slope = 0.5;
logtau = log10(tau);
logadev = log10(adev);
dlogadev = diff(logadev) ./ diff(logtau);
[~, i] = min(abs(dlogadev - slope));

% Find the y-intercept of the line.
b = logadev(i) - slope*logtau(i);

% Determine the rate random walk coefficient from the line.
logK = slope*log10(3) + b;
K = 10^logK

% Plot the results.
tauK = 3;
lineK = K .* sqrt(tau/3);
figure
loglog(tau, adev, tau, lineK, '--', tauK, K, 'o')
title('Allan Deviation with Rate Random Walk')
xlabel('\tau')
ylabel('\sigma(\tau)')
legend('\sigma', '\sigma_K')
text(tauK, K, 'K')
grid on
axis equal

K =

   9.0679e-05

Bias-Instabilität

Die Bias-Instabilität wird durch das rosa Rauschen (Flimmerrauschen)-Spektrum der Gyroskopausgabe charakterisiert. Die PSD wird vertreten durch:

$$S_{\Omega}(f) = \left\{\begin{array}{lr}(\frac{B^2}{2\pi})\frac{1}{f}&#10;&#38; : f \leq f_0\\0 &#38; : f > f_0\end{array}\right.$$

wobei

B = Bias-Instabilitätskoeffizient

$f_0$ = Grenzfrequenz

Das Einsetzen in die ursprüngliche PSD-Gleichung und Durchführen einer Integration ergibt:

$$\sigma^2(\tau) = \frac{2B^2}{\pi}[\ln{2} + \\&#10;-\frac{sin^3x}{2x^2}(sinx + 4xcosx) + Ci(2x) - Ci(4x)]$$

wobei

$x = \pi f_0\tau$

Ci = Cosinus-Integral-Funktion

Wenn $\tau$ viel länger ist als der Kehrwert der Grenzfrequenz, lautet die PSD-Gleichung:

$$\sigma^2(\tau) = \frac{2B^2}{\pi}\ln{2}$$

Die obige Gleichung ist eine Linie mit einer Steigung von 0, wenn sie in einem Log-Log-Diagramm von $\sigma(\tau)$ gegenüber $\tau$ aufgetragen wird. Der Wert von B kann mit einer Skalierung von $\sqrt{\frac{2\ln{2}}{\pi}} \approx 0.664$ direkt aus dieser Zeile abgelesen werden. Die Einheiten von B sind $rad/s$.

% Find the index where the slope of the log-scaled Allan deviation is equal
% to the slope specified.
slope = 0;
logtau = log10(tau);
logadev = log10(adev);
dlogadev = diff(logadev) ./ diff(logtau);
[~, i] = min(abs(dlogadev - slope));

% Find the y-intercept of the line.
b = logadev(i) - slope*logtau(i);

% Determine the bias instability coefficient from the line.
scfB = sqrt(2*log(2)/pi);
logB = b - log10(scfB);
B = 10^logB

% Plot the results.
tauB = tau(i);
lineB = B * scfB * ones(size(tau));
figure
loglog(tau, adev, tau, lineB, '--', tauB, scfB*B, 'o')
title('Allan Deviation with Bias Instability')
xlabel('\tau')
ylabel('\sigma(\tau)')
legend('\sigma', '\sigma_B')
text(tauB, scfB*B, '0.664B')
grid on
axis equal

B =

    0.0020

Nachdem nun alle Rauschparameter berechnet wurden, stellen Sie die Allan-Abweichung mit allen Linien dar, die zur Quantifizierung der Parameter verwendet werden.

tauParams = [tauN, tauK, tauB];
params = [N, K, scfB*B];
figure
loglog(tau, adev, tau, [lineN, lineK, lineB], '--', ...
    tauParams, params, 'o')
title('Allan Deviation with Noise Parameters')
xlabel('\tau')
ylabel('\sigma(\tau)')
legend('$\sigma (rad/s)$', '$\sigma_N ((rad/s)/\sqrt{Hz})$', ...
    '$\sigma_K ((rad/s)\sqrt{Hz})$', '$\sigma_B (rad/s)$', 'Interpreter', 'latex')
text(tauParams, params, {'N', 'K', '0.664B'})
grid on
axis equal

Gyroskop-Simulation

Verwenden Sie das imuSensor-Objekt, um Gyroskopmessungen mit den oben genannten Rauschparametern zu simulieren.

% Simulating the gyroscope measurements takes some time. To avoid this, the
% measurements were generated and saved to a MAT-file. By default, this
% example uses the MAT-file. To generate the measurements instead, change
% this logical variable to true.
generateSimulatedData = false;

if generateSimulatedData
    % Set the gyroscope parameters to the noise parameters determined
    % above. Use single-sided noise to match the parameter scaling and 500
    % poles for the bias instability model to match the hardware output.
    numpoles = 500;
    gyro = gyroparams('NoiseDensity', N, 'RandomWalk', K, ...
        'BiasInstability', B, 'NoiseType', 'single-sided', ...
        'BiasInstabilityCoefficients', fractalcoef(numpoles));
    omegaSim = helperAllanVarianceExample(L, Fs, gyro);
else
    load('SimulatedSingleAxisGyroscope', 'omegaSim')
end

Berechnen Sie die simulierte Allan-Abweichung und vergleichen Sie sie mit den protokollierten Daten.

[avarSim, tauSim] = allanvar(omegaSim, 'octave', Fs);
adevSim = sqrt(avarSim);
adevSim = mean(adevSim, 2); % Use the mean of the simulations.

figure
loglog(tau, adev, tauSim, adevSim, '--')
title('Allan Deviation of HW and Simulation')
xlabel('\tau');
ylabel('\sigma(\tau)')
legend('HW', 'SIM')
grid on
axis equal

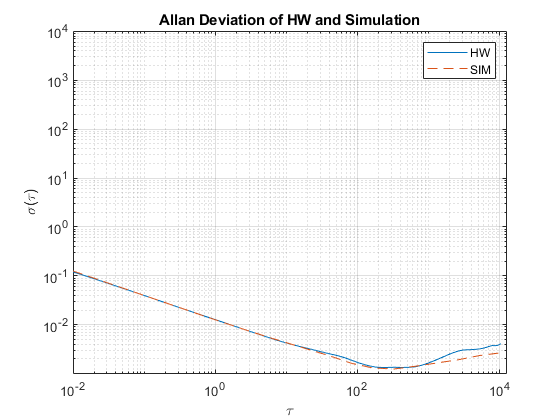
Die Darstellung zeigt, dass das aus imuSensor erstellte Gyroskopmodell Messungen mit ähnlicher Allan-Abweichung wie die protokollierten Daten generiert. Die Modellmessungen enthalten etwas weniger Rauschen, da die Quantisierungs- und temperaturbezogenen Parameter nicht mit gyroparams festgelegt werden. Mit dem Gyroskopmodell können Messungen mithilfe von Bewegungen durchgeführt werden, die mit Hardware nicht einfach erfasst werden können.

Verweise

  • IEEE-Standard. 647-2006 IEEE-Standardspezifikationsformathandbuch und Testverfahren für einachsige Laserkreisel