Schätzen Sie die Position und Ausrichtung eines Bodenfahrzeugs
Dieses Beispiel zeigt, wie die Position und Ausrichtung von Bodenfahrzeugen durch die Fusionierung von Daten einer Trägheitsmesseinheit (IMU) und eines GPS-Empfängers (Global Positioning System) geschätzt werden kann.
Simulationsaufbau
Stellen Sie die Abtastraten ein. In einem typischen System laufen der Beschleunigungsmesser und das Gyroskop in der IMU mit relativ hohen Abtastraten. Die Komplexität der Verarbeitung der Daten dieser Sensoren im Fusionsalgorithmus ist relativ gering. Im Gegensatz dazu läuft das GPS mit einer relativ niedrigen Abtastrate und die mit der Verarbeitung verbundene Komplexität ist hoch. Bei diesem Fusionsalgorithmus werden die GPS-Samples mit einer niedrigen Rate verarbeitet und die Samples des Beschleunigungsmessers und des Gyroskops werden zusammen mit der gleichen hohen Rate verarbeitet.
Um diese Konfiguration zu simulieren, wird die IMU (Beschleunigungsmesser und Gyroskop) mit 100 Hz und das GPS mit 10 Hz abgetastet.
imuFs = 100; gpsFs = 10; % Define where on the Earth this simulation takes place using latitude, % longitude, and altitude (LLA) coordinates. localOrigin = [42.2825 -71.343 53.0352]; % Validate that the |gpsFs| divides |imuFs|. This allows the sensor sample % rates to be simulated using a nested for loop without complex sample rate % matching. imuSamplesPerGPS = (imuFs/gpsFs); assert(imuSamplesPerGPS == fix(imuSamplesPerGPS), ... 'GPS sampling rate must be an integer factor of IMU sampling rate.');
Fusion Filter
Erstellen Sie den Filter, um IMU- und GPS-Messungen zu kombinieren. Der Fusionsfilter verwendet einen erweiterten Kalman-Filter, um Ausrichtung (als Quaternion), Position, Geschwindigkeit und Sensorverzerrungen zu verfolgen.
Das insfilterNonholonomic-Objekt hat zwei Hauptmethoden: predict und fusegps. Die Methode predict verwendet die Beschleunigungsmesser- und Gyroskopproben der IMU als Eingabe. Rufen Sie die Methode predict jedes Mal auf, wenn der Beschleunigungsmesser und das Gyroskop abgetastet werden. Diese Methode prognostiziert die Zustände einen Zeitschritt weiter basierend auf dem Beschleunigungsmesser und dem Gyroskop. In diesem Schritt wird die Fehlerkovarianz des erweiterten Kalman-Filters aktualisiert.
Die Methode fusegps verwendet die GPS-Samples als Eingabe. Diese Methode aktualisiert die Filterzustände basierend auf der GPS-Probe, indem sie einen Kalman-Gewinn berechnet, der die verschiedenen Sensoreingaben entsprechend ihrer Unsicherheit gewichtet. In diesem Schritt wird auch eine Fehlerkovarianz aktualisiert, dieses Mal ebenfalls unter Verwendung der Kalman-Verstärkung.
Das insfilterNonholonomic-Objekt hat zwei Haupteigenschaften: IMUSampleRate und DecimationFactor. Für das Bodenfahrzeug gelten zwei Geschwindigkeitsbeschränkungen, die davon ausgehen, dass es nicht vom Boden abprallt oder auf dem Boden gleitet. Diese Einschränkungen werden mithilfe der erweiterten Aktualisierungsgleichungen des Kalman-Filters angewendet. Diese Aktualisierungen werden mit einer Rate von IMUSampleRate/DecimationFactor Hz auf die Filterzustände angewendet.
gndFusion = insfilterNonholonomic('ReferenceFrame', 'ENU', ... 'IMUSampleRate', imuFs, ... 'ReferenceLocation', localOrigin, ... 'DecimationFactor', 2);
Flugbahn für Bodenfahrzeuge erstellen
Das waypointTrajectory-Objekt berechnet die Pose basierend auf der angegebenen Abtastrate, den Wegpunkten, den Ankunftszeiten und der Ausrichtung. Geben Sie die Parameter einer Kreisflugbahn für das Bodenfahrzeug an.
% Trajectory parameters r = 8.42; % (m) speed = 2.50; % (m/s) center = [0, 0]; % (m) initialYaw = 90; % (degrees) numRevs = 2; % Define angles theta and corresponding times of arrival t. revTime = 2*pi*r / speed; theta = (0:pi/2:2*pi*numRevs).'; t = linspace(0, revTime*numRevs, numel(theta)).'; % Define position. x = r .* cos(theta) + center(1); y = r .* sin(theta) + center(2); z = zeros(size(x)); position = [x, y, z]; % Define orientation. yaw = theta + deg2rad(initialYaw); yaw = mod(yaw, 2*pi); pitch = zeros(size(yaw)); roll = zeros(size(yaw)); orientation = quaternion([yaw, pitch, roll], 'euler', ... 'ZYX', 'frame'); % Generate trajectory. groundTruth = waypointTrajectory('SampleRate', imuFs, ... 'Waypoints', position, ... 'TimeOfArrival', t, ... 'Orientation', orientation); % Initialize the random number generator used to simulate sensor noise. rng('default');
GPS-Empfänger
Richten Sie das GPS auf die angegebene Abtastrate und den angegebenen Referenzort ein. Die anderen Parameter steuern die Art des Rauschens im Ausgangssignal.
gps = gpsSensor('UpdateRate', gpsFs, 'ReferenceFrame', 'ENU'); gps.ReferenceLocation = localOrigin; gps.DecayFactor = 0.5; % Random walk noise parameter gps.HorizontalPositionAccuracy = 1.0; gps.VerticalPositionAccuracy = 1.0; gps.VelocityAccuracy = 0.1;
IMU-Sensoren
Typischerweise verwenden Bodenfahrzeuge einen 6-Achsen-IMU-Sensor zur Lagebestimmung. Um einen IMU-Sensor zu modellieren, definieren Sie ein IMU-Sensormodell, das einen Beschleunigungsmesser und ein Gyroskop enthält. In einer realen Anwendung könnten die beiden Sensoren aus einem einzigen integrierten Schaltkreis oder aus getrennten Schaltkreisen stammen. Die hier eingestellten Eigenschaftswerte sind typisch für kostengünstige MEMS-Sensoren.
imu = imuSensor('accel-gyro', ... 'ReferenceFrame', 'ENU', 'SampleRate', imuFs); % Accelerometer imu.Accelerometer.MeasurementRange = 19.6133; imu.Accelerometer.Resolution = 0.0023928; imu.Accelerometer.NoiseDensity = 0.0012356; % Gyroscope imu.Gyroscope.MeasurementRange = deg2rad(250); imu.Gyroscope.Resolution = deg2rad(0.0625); imu.Gyroscope.NoiseDensity = deg2rad(0.025);
Initialisieren Sie die Zustände des insfilterNonholonomic
Die Zustände sind:
States Units Index Orientation (quaternion parts) 1:4 Gyroscope Bias (XYZ) rad/s 5:7 Position (NED) m 8:10 Velocity (NED) m/s 11:13 Accelerometer Bias (XYZ) m/s^2 14:16
Die Ground Truth wird zur Initialisierung der Filterzustände verwendet, sodass der Filter schnell zu guten Antworten konvergiert.
% Get the initial ground truth pose from the first sample of the trajectory % and release the ground truth trajectory to ensure the first sample is not % skipped during simulation. [initialPos, initialAtt, initialVel] = groundTruth(); reset(groundTruth); % Initialize the states of the filter gndFusion.State(1:4) = compact(initialAtt).'; gndFusion.State(5:7) = imu.Gyroscope.ConstantBias; gndFusion.State(8:10) = initialPos.'; gndFusion.State(11:13) = initialVel.'; gndFusion.State(14:16) = imu.Accelerometer.ConstantBias;
Initialisieren Sie die Varianzen von insfilterNonholonomic
Das Messrauschen beschreibt, wie stark das Rauschen die GPS-Messwerte basierend auf den gpsSensor-Parametern verfälscht und wie groß die Unsicherheit im Fahrzeugdynamikmodell ist.
Das Prozessrauschen beschreibt, wie gut die Filtergleichungen die Zustandsentwicklung beschreiben. Prozessgeräusche werden empirisch durch Parameter-Sweepen ermittelt, um die Positions- und Orientierungsschätzungen des Filters gemeinsam zu optimieren.
% Measurement noises Rvel = gps.VelocityAccuracy.^2; Rpos = gps.HorizontalPositionAccuracy.^2; % The dynamic model of the ground vehicle for this filter assumes there is % no side slip or skid during movement. This means that the velocity is % constrained to only the forward body axis. The other two velocity axis % readings are corrected with a zero measurement weighted by the % |ZeroVelocityConstraintNoise| parameter. gndFusion.ZeroVelocityConstraintNoise = 1e-2; % Process noises gndFusion.GyroscopeNoise = 4e-6; gndFusion.GyroscopeBiasNoise = 4e-14; gndFusion.AccelerometerNoise = 4.8e-2; gndFusion.AccelerometerBiasNoise = 4e-14; % Initial error covariance gndFusion.StateCovariance = 1e-9*eye(16);
Bereiche initialisieren
Der HelperScrollingPlotter-Bereich ermöglicht die Darstellung von Variablen im Zeitverlauf. Es wird hier verwendet, um Posenfehler zu verfolgen. Der HelperPoseViewer-Bereich ermöglicht eine 3D-Visualisierung der Filterschätzung und der Ground-Truth-Pose. Die Zielfernrohre können die Simulation verlangsamen. Um einen Bereich zu deaktivieren, setzen Sie die entsprechende logische Variable auf false.
useErrScope = true; % Turn on the streaming error plot usePoseView = true; % Turn on the 3D pose viewer if useErrScope errscope = HelperScrollingPlotter( ... 'NumInputs', 4, ... 'TimeSpan', 10, ... 'SampleRate', imuFs, ... 'YLabel', {'degrees', ... 'meters', ... 'meters', ... 'meters'}, ... 'Title', {'Quaternion Distance', ... 'Position X Error', ... 'Position Y Error', ... 'Position Z Error'}, ... 'YLimits', ... [-1, 1 -1, 1 -1, 1 -1, 1]); end if usePoseView viewer = HelperPoseViewer( ... 'XPositionLimits', [-15, 15], ... 'YPositionLimits', [-15, 15], ... 'ZPositionLimits', [-5, 5], ... 'ReferenceFrame', 'ENU'); end
Simulationsschleife
Die Hauptsimulationsschleife ist eine While-Schleife mit einer verschachtelten For-Schleife. Die While-Schleife wird mit gpsFs ausgeführt, was der GPS-Messrate entspricht. Die verschachtelte For-Schleife wird mit imuFs ausgeführt, was der IMU-Abtastrate entspricht. Die Oszilloskope werden mit der IMU-Abtastrate aktualisiert.
totalSimTime = 30; % seconds % Log data for final metric computation. numGPSSamples = floor(min(t(end), totalSimTime) * gpsFs); numSamples = numGPSSamples*imuSamplesPerGPS; truePosition = zeros(numSamples,3); trueOrientation = quaternion.zeros(numSamples,1); estPosition = zeros(numSamples,3); estOrientation = quaternion.zeros(numSamples,1); idx = 0; for sampleIdx = 1:numGPSSamples % Predict loop at IMU update frequency. for i = 1:imuSamplesPerGPS if ~isDone(groundTruth) idx = idx + 1; % Simulate the IMU data from the current pose. [truePosition(idx,:), trueOrientation(idx,:), ... trueVel, trueAcc, trueAngVel] = groundTruth(); [accelData, gyroData] = imu(trueAcc, trueAngVel, ... trueOrientation(idx,:)); % Use the predict method to estimate the filter state based % on the accelData and gyroData arrays. predict(gndFusion, accelData, gyroData); % Log the estimated orientation and position. [estPosition(idx,:), estOrientation(idx,:)] = pose(gndFusion); % Compute the errors and plot. if useErrScope orientErr = rad2deg( ... dist(estOrientation(idx,:), trueOrientation(idx,:))); posErr = estPosition(idx,:) - truePosition(idx,:); errscope(orientErr, posErr(1), posErr(2), posErr(3)); end % Update the pose viewer. if usePoseView viewer(estPosition(idx,:), estOrientation(idx,:), ... truePosition(idx,:), trueOrientation(idx,:)); end end end if ~isDone(groundTruth) % This next step happens at the GPS sample rate. % Simulate the GPS output based on the current pose. [lla, gpsVel] = gps(truePosition(idx,:), trueVel); % Update the filter states based on the GPS data. fusegps(gndFusion, lla, Rpos, gpsVel, Rvel); end end
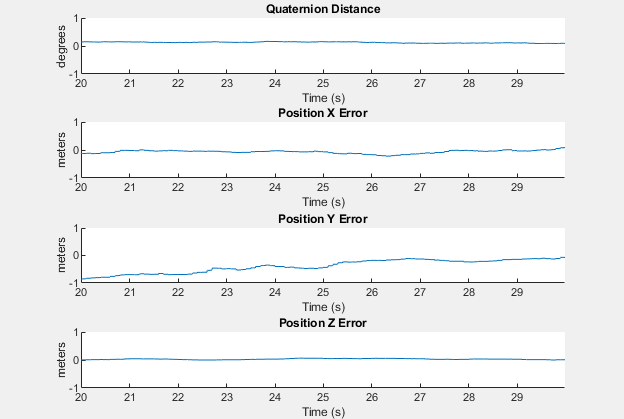
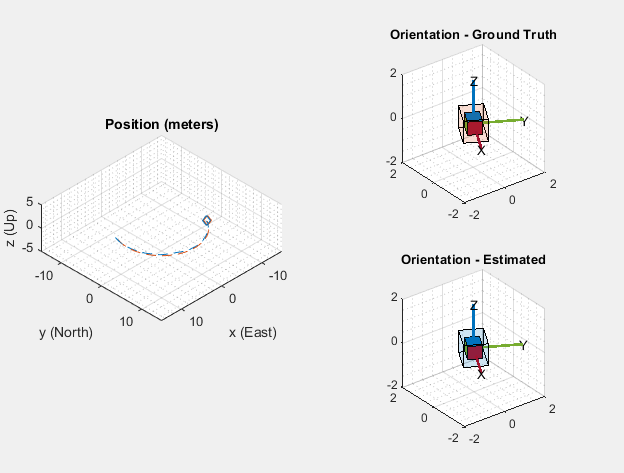
Berechnung der Fehlermetrik
Position und Ausrichtung wurden während der gesamten Simulation protokolliert. Berechnen Sie nun den mittleren quadrierten Fehler von Ende zu Ende für Position und Ausrichtung.
posd = estPosition - truePosition; % For orientation, quaternion distance is a much better alternative to % subtracting Euler angles, which have discontinuities. The quaternion % distance can be computed with the |dist| function, which gives the % angular difference in orientation in radians. Convert to degrees for % display in the command window. quatd = rad2deg(dist(estOrientation, trueOrientation)); % Display RMS errors in the command window. fprintf('\n\nEnd-to-End Simulation Position RMS Error\n');
End-to-End Simulation Position RMS Error
msep = sqrt(mean(posd.^2)); fprintf('\tX: %.2f , Y: %.2f, Z: %.2f (meters)\n\n', msep(1), ... msep(2), msep(3));
X: 1.16 , Y: 0.98, Z: 0.03 (meters)
fprintf('End-to-End Quaternion Distance RMS Error (degrees) \n');End-to-End Quaternion Distance RMS Error (degrees)
fprintf('\t%.2f (degrees)\n\n', sqrt(mean(quatd.^2)));0.11 (degrees)