Diese Seite wurde mithilfe maschineller Übersetzung übersetzt. Klicken Sie hier, um die neueste Version auf Englisch zu sehen.

allanvar

Allan Varianz

Syntax

[avar,tau] = allanvar(Omega)

[avar,tau] = allanvar(Omega,m)

[avar,tau] = allanvar(Omega,ptStr)

[avar,tau] = allanvar(___,fs)

Beschreibung

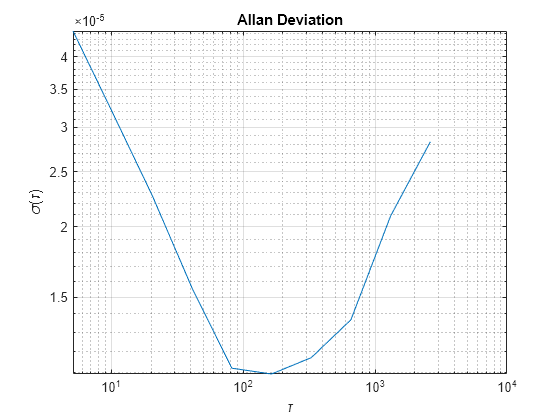
Die Allan-Varianz wird verwendet, um die Frequenzstabilität von Schwingungen für eine Datenfolge im Zeitbereich zu messen. Darüber hinaus kann damit das Eigenrauschen eines Systems als Funktion der Mittelungszeit ermittelt werden. Die Mittelungszeitreihe τ kann als τ = m/fs angegeben werden. Hier ist fs die Abtastfrequenz der Daten und m eine Liste aufsteigender Mittelwertfaktoren (wie 1, 2, 4, 8, …).

[avar,tau] = allanvar(Omega) gibt die Allan-Varianz avar als Funktion der Mittelungszeit tau zurück. Die Standard-Mittelungszeit tau ist eine Oktavfolge, die als (1, 2, ..., 2^{floor{log₂[(N-1)/2]}}) angegeben ist, wobei N die Anzahl der Samples in Omega ist. Wenn Omega als Matrix angegeben ist, operiert allanvar über die Spalten von omega.

[avar,tau] = allanvar(Omega,m) gibt die Allan-Varianz avar für bestimmte Werte von tau zurück, die durch m definiert sind. Da die Standardfrequenz fs als 1 angenommen wird, ist die Ausgabe tau genau dieselbe wie m.

[avar,tau] = allanvar(Omega,ptStr) setzt den Mittelwertfaktor m auf die angegebene Punktspezifikation ptStr. Da die Standardfrequenz fs 1 ist, ist die Ausgabe tau genau gleich der angegebenen m. ptStr kann als 'octave' oder 'decade' angegeben werden.

[avar,tau] = allanvar(___,fs) ermöglicht Ihnen außerdem, die Abtastfrequenz fs der Eingabedaten omega in Hz anzugeben. Dieser Eingabeparameter kann mit jeder der vorherigen Syntaxen verwendet werden.

Beispiele

Bestimmen Sie die Allan-Varianz eines einachsigen Gyroskops

Laden Sie Gyroskopdaten aus einer MAT-Datei, einschließlich der Abtastrate der Daten in Hz. Berechnen Sie die Allan-Varianz.

load('LoggedSingleAxisGyroscope','omega','Fs')
[avar,tau] = allanvar(omega,'octave',Fs);

Zeichnen Sie die Allan-Varianz in einem loglog-Diagramm auf.

loglog(tau,avar)
xlabel('\tau')
ylabel('\sigma^2(\tau)')
title('Allan Variance')
grid on

Bestimmen Sie die Allan-Abweichung bei bestimmten Werten von $\tau$

Generieren Sie ein Beispiel für Gyroskoprauschen, einschließlich Winkel-Irrfahrt und Raten-Irrfahrt.

numSamples = 1e6;
Fs = 100;
nStd = 1e-3;
kStd = 1e-7;
nNoise = nStd.*randn(numSamples,1);
kNoise = kStd.*cumsum(randn(numSamples,1));
omega = nNoise+kNoise;

Berechnen Sie die Allan-Abweichung bei bestimmten Werten von $\mathit{m}=\tau$. Die Allan-Abweichung ist die Quadratwurzel der Allan-Varianz.

m = 2.^(9:18);
[avar,tau] = allanvar(omega,m,Fs);
adev = sqrt(avar);

Zeichnen Sie die Allan-Abweichung in einem loglog-Diagramm auf.

loglog(tau,adev)
xlabel('\tau')
ylabel('\sigma(\tau)')
title('Allan Deviation')
grid on

Eingabeargumente

Omega — Eingabedaten

N-mal-1-Vektor | N-mal-M-Matrix

Eingabedaten, angegeben als N-mal-1-Vektor oder als N-mal-M-Matrix. N ist die Anzahl der Samples und M die Anzahl der Sample-Sets. Wenn es als Matrix angegeben ist, operiert allanvar über die Spalten von Omega.

Datentypen: single | double

m — Mittelungsfaktor

Skalar | Vektor

Mittelwertfaktor, angegeben als Skalar oder Vektor mit aufsteigenden ganzzahligen Werten kleiner als (N-1)/2, wobei N die Anzahl der Samples in Omega ist.

Datentypen: single | double

ptStr — Punktspezifikation von m

'octave' (Standardeinstellung) | 'decade'

Punktspezifikation von m, angegeben als 'octave' oder 'decade'. Basierend auf dem Wert von ptStr wird m wie folgt angegeben:

• Wenn ptStr als 'octave' angegeben wird, ist m:

  $$\left[2^0,2^1{\mathrm{...2}}^{\lfloor {\log }_2\left(\frac{N-1}{2}\right)\rfloor }\right]$$

• Wenn ptStr als 'decade' angegeben wird, ist m:

  $$\left[{10}^0,{10}^1{\mathrm{...10}}^{\lfloor {\log }_{10}\left(\frac{N-1}{2}\right)\rfloor }\right]$$

N ist die Anzahl der Samples in Omega.

fs — Grundfrequenz der Eingangsdaten in Hz

Skalar

Grundfrequenz der Eingabedaten, Omega, in Hz, angegeben als positiver Skalar.

Datentypen: single | double

Ausgabeargumente

avar — Allan-Varianz der Eingabedaten

Vektor | Matrix

Alle Varianzen der Eingabedaten bei tau, zurückgegeben als Vektor oder Matrix.

tau — Mittelungszeit der Allan-Varianz

Vektor | Matrix

Mittelungszeit der Allan-Varianz, zurückgegeben als Vektor oder Matrix.

Versionsverlauf

Eingeführt in R2019a

Siehe auch

gyroparams | imuSensor