Linearize Simulink Models
Generally, real systems are nonlinear. To design an MPC controller for a nonlinear system, you can model the plant in Simulink®.
Although an MPC controller can regulate a nonlinear plant, the model used within the controller must be linear. In other words, the controller employs a linear approximation of the nonlinear plant. The accuracy of this approximation significantly affects controller performance.
To obtain such a linear approximation, you linearize the nonlinear plant at a specified operating point.
Note
The following examples require Simulink Control Design™ software.
You can linearize a Simulink model:
From the command line.
Using the Model Linearizer.
Using MPC Designer. For an example, see Linearize Simulink Models Using MPC Designer.
Linearization Using MATLAB Code
This example shows how to obtain a linear model of a plant using a MATLAB® script.
For this example the CSTR model, CSTR_OpenLoop, is linearized. The model inputs are the coolant temperature (manipulated variable of the MPC controller), limiting reactant concentration in the feed stream, and feed temperature. The model states are the temperature and concentration of the limiting reactant in the product stream. Both states are measured and used for feedback control.
Obtain Steady-State Operating Point
The operating point defines the nominal conditions at which you linearize a model. It is usually a steady-state condition.
Suppose that you plan to operate the CSTR with the output concentration, C_A, at . The nominal feed concentration is , and the nominal feed temperature is 300 K.
Create and visualize an operating point specification object to define the steady-state conditions.
opspec = operspec('CSTR_OpenLoop'); opspec = addoutputspec(opspec,'CSTR_OpenLoop/CSTR',2); opspec.Outputs(1).Known = true; opspec.Outputs(1).y = 2; opspec
opspec =
Operating point specification for the Model CSTR_OpenLoop.
(Time-Varying Components Evaluated at time t=0)
States:
----------
x Known SteadyState Min Max dxMin dxMax
___________ ___________ ___________ ___________ ___________ ___________ ___________
(1.) CSTR_OpenLoop/CSTR/C_A
8.5695 false true 0 Inf -Inf Inf
(2.) CSTR_OpenLoop/CSTR/T_K
311.267 false true 0 Inf -Inf Inf
Inputs:
----------
u Known Min Max
_____ _____ _____ _____
(1.) CSTR_OpenLoop/Coolant Temperature
0 false -Inf Inf
Outputs:
----------
y Known Min Max
_____ _____ _____ _____
(1.) CSTR_OpenLoop/CSTR
2 true -Inf Inf
Search for an operating point that satisfies the specifications.
op1 = findop('CSTR_OpenLoop',opspec);Operating point search report: ---------------------------------
opreport =
Operating point search report for the Model CSTR_OpenLoop.
(Time-Varying Components Evaluated at time t=0)
Operating point specifications were successfully met.
States:
----------
Min x Max dxMin dx dxMax
___________ ___________ ___________ ___________ ___________ ___________
(1.) CSTR_OpenLoop/CSTR/C_A
0 2 Inf 0 -4.6683e-12 0
(2.) CSTR_OpenLoop/CSTR/T_K
0 373.1311 Inf 0 5.5678e-11 0
Inputs:
----------
Min u Max
________ ________ ________
(1.) CSTR_OpenLoop/Coolant Temperature
-Inf 299.0349 Inf
Outputs:
----------
Min y Max
___ ___ ___
(1.) CSTR_OpenLoop/CSTR
2 2 2
The calculated operating point is C_A = and T_K = 373 K. Notice that the steady-state coolant temperature is also given as 299 K, which is the nominal value of the input used to control the plant.
To specify:
Values of known inputs, use the
Input.KnownandInput.ufields ofopspecInitial guesses for state values, use the
State.xfield ofopspec
For example, the following code specifies the coolant temperature as 305 K and initial guess values of the C_A and T_K states before calculating the steady-state operating point:
opspec = operspec('CSTR_OpenLoop'); opspec.States(1).x = 1; opspec.States(2).x = 400; opspec.Inputs(1).Known = true; opspec.Inputs(1).u = 305; op2 = findop('CSTR_OpenLoop',opspec)
Operating point search report: ---------------------------------
opreport =
Operating point search report for the Model CSTR_OpenLoop.
(Time-Varying Components Evaluated at time t=0)
Operating point specifications were successfully met.
States:
----------
Min x Max dxMin dx dxMax
___________ ___________ ___________ ___________ ___________ ___________
(1.) CSTR_OpenLoop/CSTR/C_A
0 1.7787 Inf 0 0 0
(2.) CSTR_OpenLoop/CSTR/T_K
0 376.5371 Inf 0 -9.9476e-14 0
Inputs:
----------
Min u Max
___ ___ ___
(1.) CSTR_OpenLoop/Coolant Temperature
305 305 305
Outputs: None
----------
op2 =
Operating point for the Model CSTR_OpenLoop.
(Time-Varying Components Evaluated at time t=0)
States:
----------
x
________
(1.) CSTR_OpenLoop/CSTR/C_A
1.7787
(2.) CSTR_OpenLoop/CSTR/T_K
376.5371
Inputs:
----------
u
___
(1.) CSTR_OpenLoop/Coolant Temperature
305
Specify Linearization Inputs and Outputs
If the linearization input and output signals are already defined in the model, as in CSTR_OpenLoop, then use the following to obtain the signal set.
io = getlinio('CSTR_OpenLoop');Otherwise, specify the input and output signals as shown here.
io(1) = linio('CSTR_OpenLoop/Coolant Temperature',1,'input'); io(2) = linio('CSTR_OpenLoop/Feed Concentration',1,'input'); io(3) = linio('CSTR_OpenLoop/Feed Temperature',1,'input'); io(4) = linio('CSTR_OpenLoop/CSTR',1,'output'); io(5) = linio('CSTR_OpenLoop/CSTR',2,'output');
Linearize Model
Linearize the model using the specified operating point, op1, and input/output signals, io.
sys = linearize('CSTR_OpenLoop',op1,io)sys =
A =
C_A T_K
C_A -5 -0.3427
T_K 47.68 2.785
B =
Coolant Temp Feed Concent Feed Tempera
C_A 0 1 0
T_K 0.3 0 1
C =
C_A T_K
CSTR/1 0 1
CSTR/2 1 0
D =
Coolant Temp Feed Concent Feed Tempera
CSTR/1 0 0 0
CSTR/2 0 0 0
Continuous-time state-space model.
Model Properties
Linearize the model also around the operating point, op2, using the same input/output signals.
sys = linearize('CSTR_OpenLoop',op2,io)sys =
A =
C_A T_K
C_A -5.622 -0.3458
T_K 55.1 2.822
B =
Coolant Temp Feed Concent Feed Tempera
C_A 0 1 0
T_K 0.3 0 1
C =
C_A T_K
CSTR/1 0 1
CSTR/2 1 0
D =
Coolant Temp Feed Concent Feed Tempera
CSTR/1 0 0 0
CSTR/2 0 0 0
Continuous-time state-space model.
Model Properties
Linearization Using Model Linearizer in Simulink Control Design
This example shows how to linearize a Simulink model using the Model Linearizer, provided by the Simulink Control Design software.
Open Simulink Model
This example uses the CSTR model, CSTR_OpenLoop.
open_system('CSTR_OpenLoop')Specify Linearization Inputs and Outputs
The linearization inputs and outputs are already specified for
CSTR_OpenLoop. The input signals correspond to the outputs from the
Feed Concentration, Feed Temperature, and
Coolant Temperature blocks. The output signals are the inputs to
the CSTR Temperature and Residual Concentration
blocks.
To specify a signal as a linearization input or output, first in the Simulink Apps tab, click Linearization Manager. Then, in the Simulink model window, click the signal. Finally, in the Insert Analysis Points gallery, in the Closed Loop section, select either Input Perturbation for a linearization input or Output Measurement for a linearization output.
Open Model Linearizer
To open the Model Linearizer, in the Apps tab, click Model Linearizer.
Specify Residual Concentration as Known Trim Constraint
To specify the residual concentration as a known trim constant, first in the
Simulink
Apps tab, click Linearization Manager. Then,
in the Simulink model window, click the CA output signal from the
CSTR block. Finally, in the Insert Analysis
Points gallery, in the Trim section, select
Trim Output Constraint.
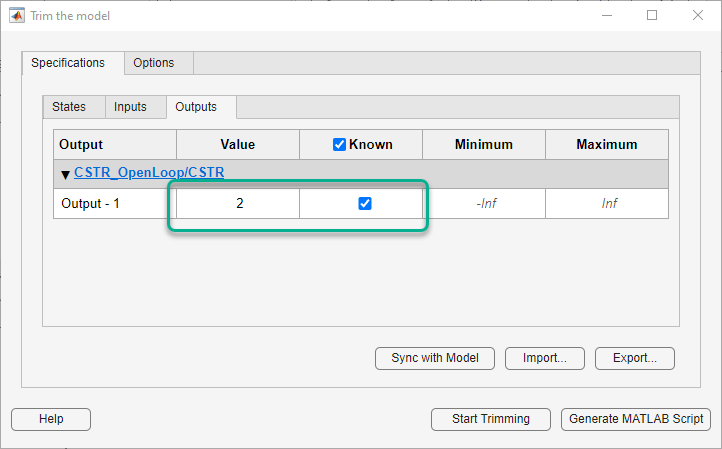
In the Model Linearizer, on the Linear Analysis tab, select Operating Point > Trim Model.
In the Trim the model dialog box, on the Outputs tab:
Select the Known check box for
Channel - 1under CSTR_OpenLoop/CSTR.Set the corresponding Value to
2kmol/m3.
Create and Verify Operating Point
In the Trim the model dialog box, click Start trimming.
The Trim progress viewer window opens up showing the optimization progress towards finding a point in the state-input space of the model with the characteristics specified in the States, Inputs, and Outputs tabs. After the optimization process terminates, close the trim progress window as well as the Trim the model dialog box.
The operating point op_trim1 displays in the Linear
Analysis Workspace of Model Linearizer. Select
op_trim1 to display basic information in the Linear
Analysis Workspace section.
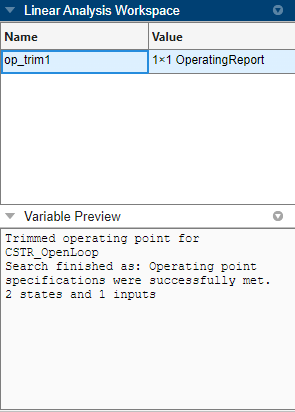
Double click op_trim1 to view the resulting operating point in
the Edit dialog box.
In the Edit dialog box, select the Input tab.
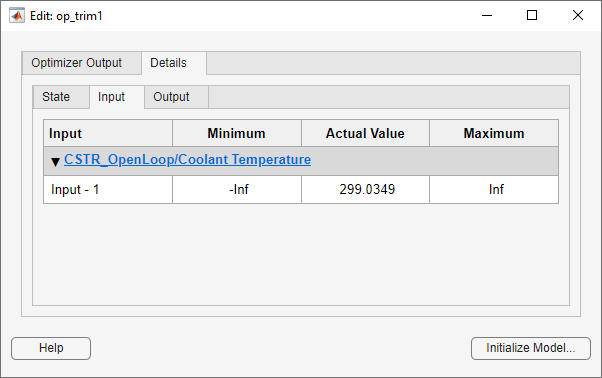
The coolant temperature at steady state is 299 K, as desired. Close the Edit dialog box.
Linearize Model
On the Linear Analysis tab, in the Operating
Point drop-down list, make sure op_trim1 is
selected.
In the Linearize section, click ![]() Step to linearize the Simulink model and display the step response of the linearized model.
Step to linearize the Simulink model and display the step response of the linearized model.
This option creates the linear model linsys1 in the
Linear Analysis Workspace and generates a step response for this
model. linsys1 uses op_trim1 as its operating
point.
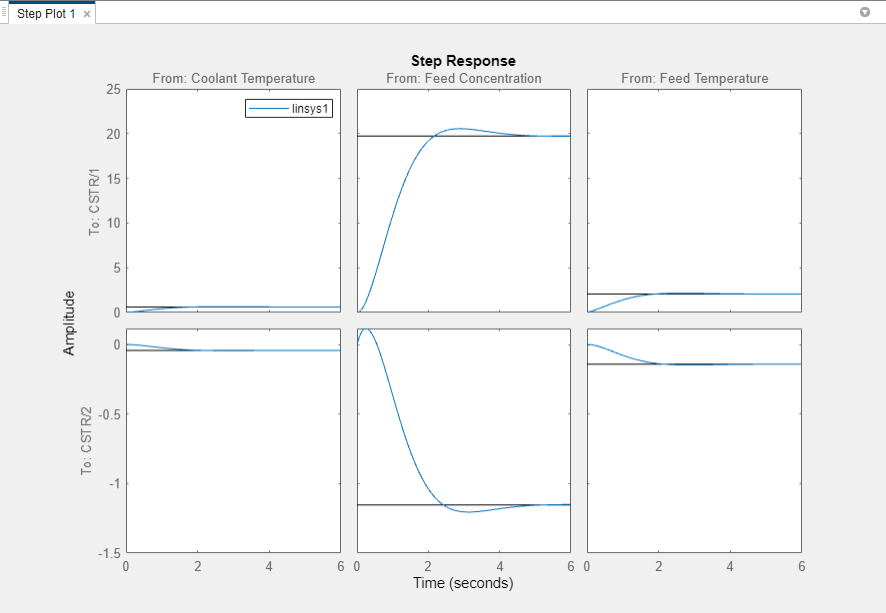
The step response from feed concentration to output CSTR/2
displays an interesting inverse response. An examination of the linear model shows that
CSTR/2 is the residual CSTR concentration, C_A.
When the feed concentration increases, C_A increases initially
because more reactant is entering, which increases the reaction rate. This rate increase
results in a higher reactor temperature (output CSTR/1), which
further increases the reaction rate and C_A decreases
dramatically.
Export Linearization Result
If necessary, you can repeat any of these steps to improve your model performance. Once you are satisfied with your linearization result, in the Model Linearizer, drag the linear model from the Linear Analysis Workspace section of Model Linearizer to the MATLAB Workspace section just above it. You can now use your linear model to design an MPC controller.
See Also
Apps
- Model Linearizer (Simulink Control Design) | MPC Designer
Functions
linearize(Simulink Control Design)