mkpp

Make piecewise polynomial

Syntax

pp = mkpp(breaks,coefs)

pp = mkpp(breaks,coefs,d)

Description

pp = mkpp(breaks,coefs) builds a piecewise polynomial pp from its breaks and coefficients. Use ppval to evaluate the piecewise polynomial at specific points, or unmkpp to extract details about the piecewise polynomial.

pp = mkpp(breaks,coefs,d) specifies that the piecewise polynomial is vector-valued, such that the value of each of its coefficients is a vector of length d.

Examples

Create Piecewise Polynomial with Polynomials of Several Degrees

Create a piecewise polynomial that has a cubic polynomial in the interval [0,4], a quadratic polynomial in the interval [4,10], and a quartic polynomial in the interval [10,15].

breaks = [0 4 10 15];
coefs = [0 1 -1 1 1; 0 0 1 -2 53; -1 6 1 4 77];
pp = mkpp(breaks,coefs)

pp = struct with fields:
      form: 'pp'
    breaks: [0 4 10 15]
     coefs: [3×5 double]
    pieces: 3
     order: 5
       dim: 1

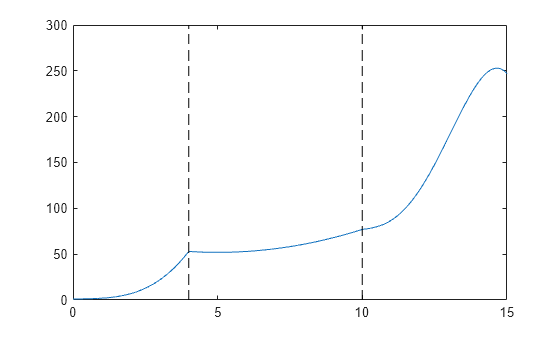
Evaluate the piecewise polynomial at many points in the interval [0,15] and plot the results. Plot vertical dashed lines at the break points where the polynomials meet.

xq = 0:0.01:15;
plot(xq,ppval(pp,xq))
line([4 4],ylim,'LineStyle','--','Color','k')
line([10 10],ylim,'LineStyle','--','Color','k')

Create Piecewise Polynomial with Repeated Pieces

Create and plot a piecewise polynomial with four intervals that alternate between two quadratic polynomials.

The first two subplots show a quadratic polynomial and its negation shifted to the intervals [-8,-4] and [-4,0]. The polynomial is

$$1-{(\frac{x}{2}-1)}^2=\frac{-x^2}{4}+x.$$

The third subplot shows a piecewise polynomial constructed by alternating these two quadratic pieces over four intervals. Vertical lines are added to show the points where the polynomials meet.

subplot(2,2,1)
cc = [-1/4 1 0]; 
pp1 = mkpp([-8 -4],cc);
xx1 = -8:0.1:-4; 
plot(xx1,ppval(pp1,xx1),'k-')

subplot(2,2,2)
pp2 = mkpp([-4 0],-cc);
xx2 = -4:0.1:0; 
plot(xx2,ppval(pp2,xx2),'k-')

subplot(2,1,2)
pp = mkpp([-8 -4 0 4 8],[cc;-cc;cc;-cc]);
xx = -8:0.1:8;
plot(xx,ppval(pp,xx),'k-')
hold on
line([-4 -4],ylim,'LineStyle','--')
line([0 0],ylim,'LineStyle','--')
line([4 4],ylim,'LineStyle','--')
hold off

Input Arguments

breaks — Break points

vector

Break points, specified as a vector of length L+1 with strictly increasing elements that represent the start and end of each of L intervals.

Data Types: single | double

coefs — Polynomial coefficients

matrix

Polynomial coefficients, specified as an L-by-k matrix with the ith row coefs(i,:) containing the local coefficients of an order k polynomial on the ith interval, [breaks(i), breaks(i+1)]. In other words, the polynomial is coefs(i,1)*(X-breaks(i))^(k-1) + coefs(i,2)*(X-breaks(i))^(k-2) + ... + coefs(i,k-1)*(X-breaks(i)) + coefs(i,k).

Data Types: single | double

d — Dimension

scalar | vector

Dimension, specified as a scalar or vector of integers. Specify d to signify that the piecewise polynomial has coefficient values of size d.

Data Types: single | double

Output Arguments

pp — Piecewise polynomial

structure

Piecewise polynomial, returned as a structure. Use this structure with the ppval function to evaluate the piecewise polynomial at one or more query points. The structure has these fields.

Field	Description
form	'pp' for piecewise polynomial
breaks	Vector of length L+1 with strictly increasing elements that represent the start and end of each of L intervals
coefs	L-by-k matrix with each row coefs(i,:) containing the local coefficients of an order k polynomial on the ith interval, [breaks(i),breaks(i+1)]
pieces	Number of pieces, L
order	Order of the polynomials
dim	Dimensionality of target

Since the polynomial coefficients in coefs are local coefficients for each interval, you must subtract the lower endpoint of the corresponding knot interval to use the coefficients in a conventional polynomial equation. In other words, for the coefficients [a,b,c,d] on the interval [x1,x2], the corresponding polynomial is

$$f\left(x\right)=a{\left(x-x_1\right)}^3+b{\left(x-x_1\right)}^2+c\left(x-x_1\right)+d.$$

Extended Capabilities

C/C++ Code Generation

Generate C and C++ code using MATLAB® Coder™.

Usage notes and limitations:

• The output structure pp differs from the pp structure in MATLAB^®. In MATLAB, ppval cannot use the pp structure from the code generator. For code generation, ppval cannot use a pp structure created by MATLAB. unmkpp can use a MATLAB pp structure for code generation.

  To create a MATLAB pp structure from a pp structure created by the code generator:

  • In code generation, use unmkpp to return the piecewise polynomial details to MATLAB.

  • In MATLAB, use mkpp to create the pp structure.

• If you do not provide d, then coefs must be two-dimensional and have a fixed number of columns. In this case, the number of columns is the order.

• To define a piecewise constant polynomial, coefs must be a column vector or d must have at least two elements.

• If you provide d and d is 1, then d must be a constant. Otherwise, if the input to ppval is nonscalar, then the shape of the output of ppval can differ from ppval in MATLAB.

• If you provide d, then it must have a fixed length. One of the following sets of statements must be true:

  1. Suppose that m = length(d) and npieces = length(breaks) - 1.

     size(coefs,j) = d(j) 
     size(coefs,m+1) = npieces
     size(coefs,m+2) = order 

     j = 1,2,...,m. The dimension m+2 must be fixed length.

  2. Suppose that m = length(d) and npieces = length(breaks) - 1.

     size(coefs,1) = prod(d)*npieces
     size(coefs,2) = order             

     The second dimension must be fixed length.

• If you do not provide d, then the following statements must be true:

  Suppose that m = length(d) and npieces = length(breaks) - 1.

  size(coefs,1) = prod(d)*npieces
  size(coefs,2) = order

  The second dimension must be fixed length.

Thread-Based Environment

Run code in the background using MATLAB® backgroundPool or accelerate code with Parallel Computing Toolbox™ ThreadPool.

This function fully supports thread-based environments. For more information, see Run MATLAB Functions in Thread-Based Environment.

Version History

Introduced before R2006a