layout
Change layout of graph plot
Description
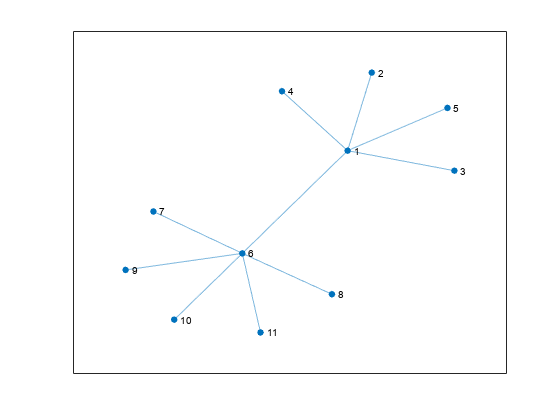
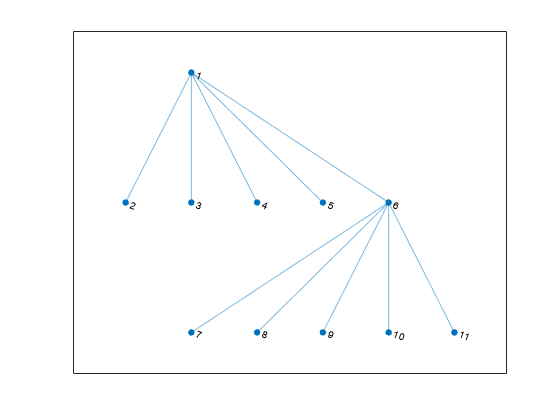
layout( changes the layout of graph
plot H)H by using an automatic choice of layout method based on the
structure of the graph. The layout function modifies the
XData and YData properties of
H.
layout(
uses additional options specified by one or more name-value pair arguments. For
example, H,method,Name,Value)layout(H,'force','Iterations',N) specifies the number of
iterations to use in computing the force layout, and
layout(H,'layered','Sources',S) uses a layered layout with
source nodes S included in the first layer.
Examples
Input Arguments
Name-Value Arguments
Tips
Use the
Layoutname-value pair to change the layout of a graph when you plot it. For example,plot(G,'Layout','circle')plots the graphGwith a circular layout.When using the
'force'or'force3'layout methods, a best practice is to use more iterations with the algorithm instead of usingXStart,YStart, andZStartto restart the algorithm using previous outputs. The result of executing the algorithm with 100 iterations is different in comparison to executing 50 iterations, and then restarting the algorithm from the ending positions to execute 50 more iterations.
References
[1] Fruchterman, T., and E. Reingold,. “Graph Drawing by Force-directed Placement.” Software — Practice & Experience. Vol. 21 (11), 1991, pp. 1129–1164.
[2] Gansner, E., E. Koutsofios, S. North, and K.-P Vo. “A Technique for Drawing Directed Graphs.” IEEE Transactions on Software Engineering. Vol.19, 1993, pp. 214–230.
[3] Barth, W., M. Juenger, and P. Mutzel. “Simple and Efficient Bilayer Cross Counting.” Journal of Graph Algorithms and Applications. Vol.8 (2), 2004, pp. 179–194.
[4] Brandes, U., and B. Koepf. “Fast and Simple Horizontal Coordinate Assignment.” LNCS. Vol. 2265, 2002, pp. 31–44.
[5] Y. Koren. “Drawing Graphs by Eigenvectors: Theory and Practice.” Computers and Mathematics with Applications. Vol. 49, 2005, pp. 1867–1888.
Version History
Introduced in R2015b