transreduction
Transitive reduction
Syntax
Description
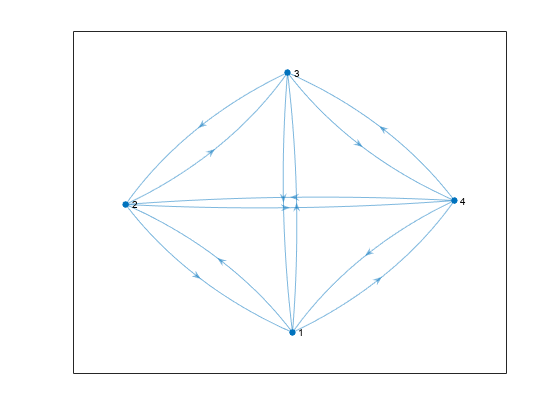
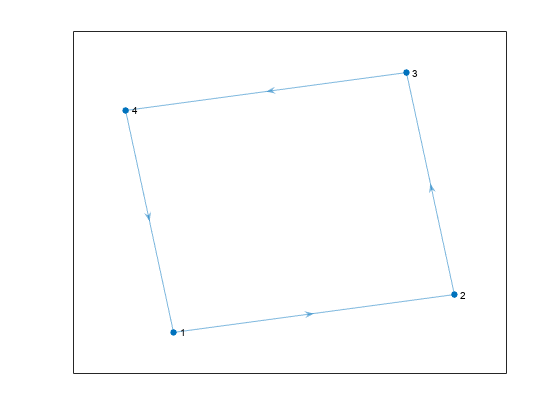
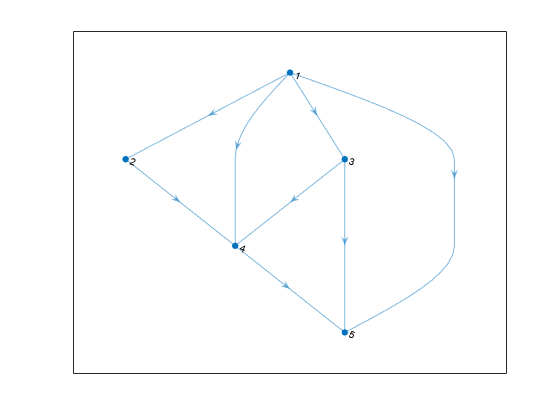
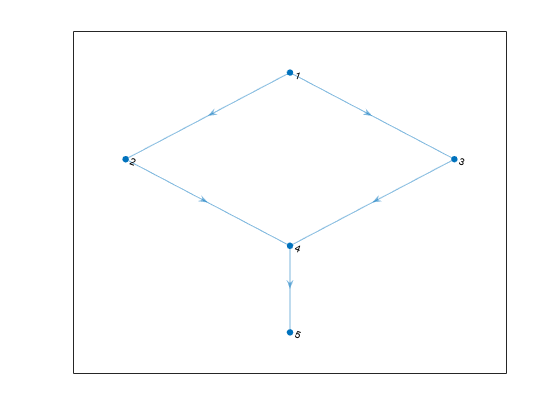
H = transreduction(G)G as a new graph, H. The nodes in
H are the same as those in G, but
H has different edges. H contains the
fewest number of edges such that if there is a path from node i
to node j in G, then there is also a path from
node i to node j in
H.
Examples
Input Arguments
Output Arguments
More About
Version History
Introduced in R2015b