cylinder
Create cylinder
Syntax
Description
Create Cylinder Data
[X,Y,Z] = cylinder returns three
2-by-21 matrices containing the
x-, y-, and z-
coordinates of a cylinder without drawing it. The cylinder has a radius of 1 and
20 equally spaced points around its circumference. The bases are parallel to the
xy-plane.
To draw the cylinder, pass X, Y, and
Z to the surf or
mesh function.
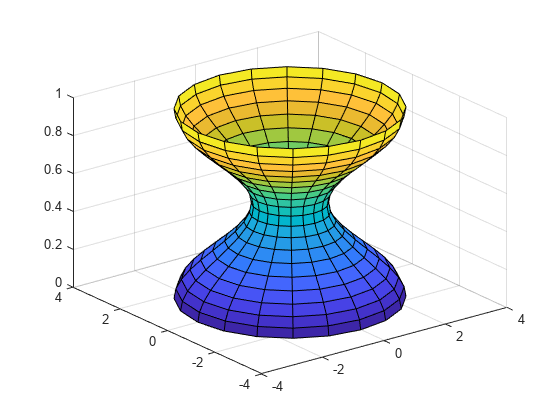
[X,Y,Z] = cylinder( returns the
x-, y-, and z-
coordinates of a cylinder with the specified profile curve,
r)r, and 20 equally spaced points around its
circumference. The function treats each element in r as a
radius at equally spaced heights along the unit height of the cylinder. The size
of each coordinate matrix is m-by-21,
where m=numel(r). However, if r is a
scalar, then m=2.
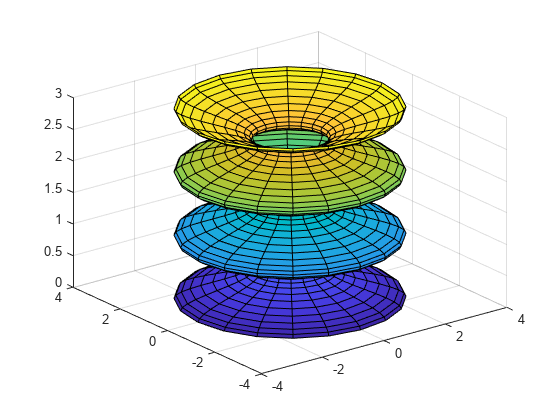
Plot Cylinders
cylinder(___) plots a cylinder without
returning the coordinates. Use this syntax with any of the input arguments in
previous syntaxes.
cylinder(___,
sets properties of the cylinder plot using one or more name-value arguments. For
example, you can specify the color and transparency of the cylinder. For a list
of properties, see Surface Properties. (since R2024b)Name=Value)
cylinder( plots
into the axes specified by ax,___)ax instead of the current axes.
Specify the axes as the first input argument.