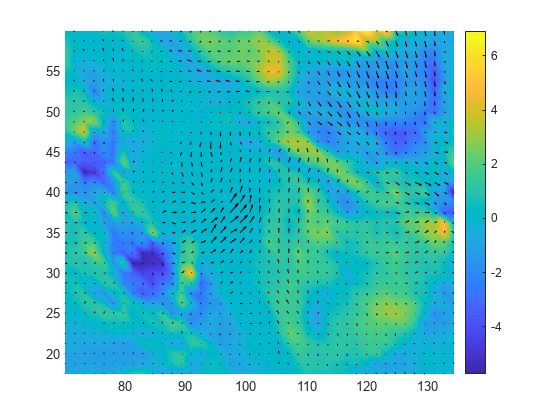
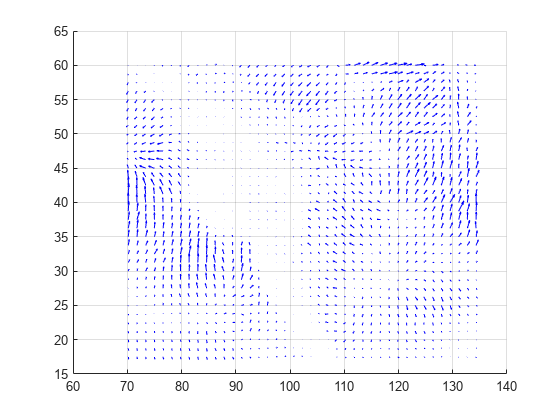
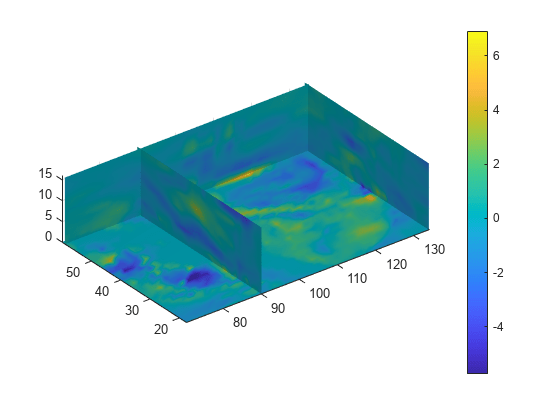
curl
Curl and angular velocity of vector field
Syntax
Description
[
computes the numerical curl and
angular velocity of a 3-D vector field with vector components
curlx,curly,curlz,cav] = curl(X,Y,Z,Fx,Fy,Fz)Fx, Fy, and Fz. The output
curlx, curly, and curlz
represent the vector components of the curl, and cav represents the
angular velocity of the curl.
The arrays X, Y, and Z, which
define the coordinates for the vector components Fx,
Fy, and Fz, must be monotonic, but do not need to
be uniformly spaced. X, Y, and Z
must be 3-D arrays of the same size, which can be produced by meshgrid.
[
assumes a default grid of sample points. The default grid points curlx,curly,curlz,cav] = curl(Fx,Fy,Fz)X,
Y, and Z are determined by the expression
[X,Y,Z] = meshgrid(1:n,1:m,1:p), where [m,n,p] =
size(Fx). Use this syntax when you want to conserve memory and are not
concerned about the absolute distances between points.
[
computes the numerical curl and
angular velocity of a 2-D vector field with vector components
curlz,cav] = curl(X,Y,Fx,Fy)Fx and Fy. The output curlz
represents the z-component of the curl, and cav
represents the angular velocity of the curl.
The matrices X and Y, which define the
coordinates for Fx and Fy, must be monotonic, but do
not need to be uniformly spaced. X and Y must be 2-D
matrices of the same size, which can be produced by meshgrid.
Examples
Input Arguments
Output Arguments
More About
Algorithms
curl computes the partial derivatives in its definition by using finite
differences. For interior data points, the partial derivatives are calculated using
central difference. For data points along the edges, the partial
derivatives are calculated using single-sided (forward)
difference.
For example, consider a 2-D vector field F that is represented by the matrices Fx and
Fy at locations X and Y with size
m-by-n. The locations are 2-D grids created by
[X,Y] = meshgrid(x,y), where x is a vector of length
n and y is a vector of length m.
curl then computes the partial derivatives ∂Fy /
∂x and ∂Fx /
∂y as
dFy_dx(:,i) = (Fy(:,i+1) - Fy(:,i-1))/(x(i+1) - x(i-1))anddFx_dy(j,:) = (Fx(j+1,:) - Fx(j-1,:))/(y(j+1) - y(j-1))for interior data points.
dFy_dx(:,1) = (Fy(:,2) - Fy(:,1))/(x(2) - x(1))anddFy_dx(:,n) = (Fy(:,n) - Fy(:,n-1))/(x(n) - x(n-1))for data points at the left and right edges.
dFx_dy(1,:) = (Fx(2,:) - Fx(1,:))/(y(2) - y(1))anddFx_dy(m,:) = (Fx(m,:) - Fx(m-1,:))/(y(m) - y(m-1))for data points at the top and bottom edges.
The numerical curl of the vector field is equal to curlz = dFy_dx -
dFx_dy and the angular velocity is cav = 0.5*curlz.
Extended Capabilities
Version History
Introduced before R2006a