boundary
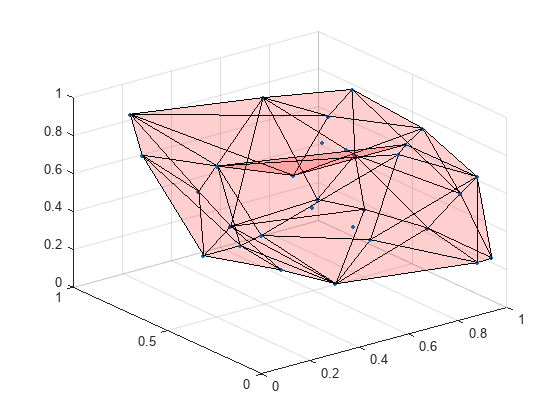
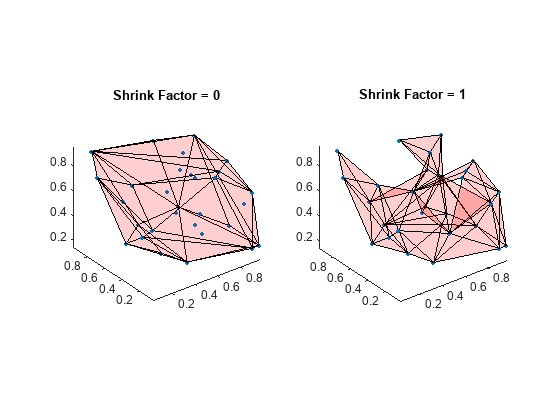
Boundary of a set of points in 2-D or 3-D
Description
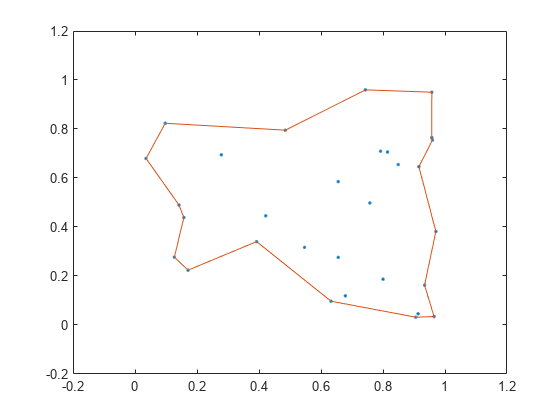
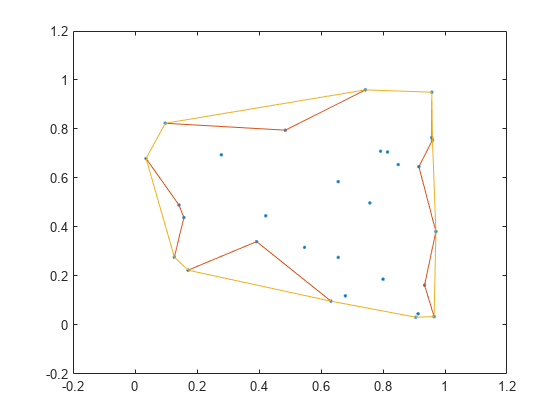
Examples
Input Arguments
Output Arguments
Algorithms
boundary constructs an alphaShape from the specified points and then uses boundaryFacets to determine which points lie on the boundary.
Extended Capabilities
Version History
Introduced in R2014b
See Also
alphaShape | triangulation | delaunayTriangulation | trisurf | convhull