alphaSpectrum

Alpha values giving distinct alpha shapes

Syntax

a = alphaSpectrum(shp)

Description

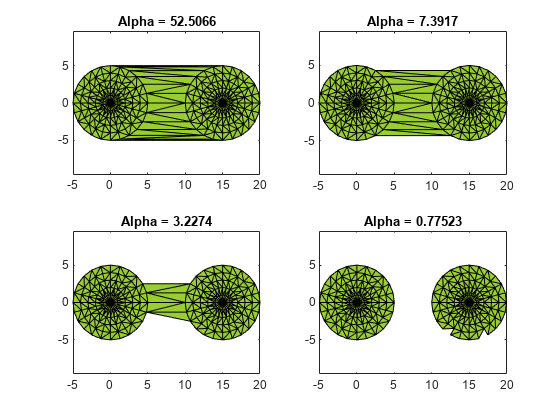
a = alphaSpectrum(shp) returns the values of the alpha radius that produce distinct alpha shapes. a is in descending sorted order. Each element in a represents a value of the alpha radius that results in a distinct shape. The length of a is equal to the number of unique shapes. Values of alpha that lie between the values in a do not produce unique alpha shapes.

Examples

Find Alpha Spectrum for 2-D Point Cloud

Create and plot a set of 2-D points.

th = (pi/12:pi/12:2*pi)';
x1 = [reshape(cos(th)*(1:5), numel(cos(th)*(1:5)),1); 0];
y1 = [reshape(sin(th)*(1:5), numel(sin(th)*(1:5)),1); 0];
x = [x1; x1+15;];
y = [y1; y1];
plot(x,y,'.')
axis equal

Create an alpha shape for the point cloud using the default alpha radius.

shp = alphaShape(x,y);

Find the spectrum of critical alpha values that produce unique alpha shapes for the point cloud.

alphaspec = alphaSpectrum(shp);

Plot four of the unique alpha shapes generated by alpha values in the spectrum.

for k = 1:4
    alpha = alphaspec(8*k-7); 
    shp.Alpha = alpha; 
    subplot(2,2,k)
    plot(shp)
    title("Alpha = "+alpha)
end

Input Arguments

shp — Alpha shape

alphaShape object

Alpha shape, specified as an alphaShape object. For more information, see alphaShape.

Example: shp = alphaShape(x,y) creates a 2-D alphaShape object from the (x,y) point coordinates.

Output Arguments

a — Alpha values for distinct alpha shapes

column vector

Alpha values for distinct alpha shapes, returned as a column vector in descending sorted order.

Version History

Introduced in R2014b