bwferet
Measure Feret properties
Syntax
Description
out = bwferet(BW,properties)properties specifies the Feret properties to be
measured for each object in input binary image BW. The measured Feret
properties include the minimum and maximum Feret diameters, Feret angles, and endpoint
coordinates of Feret diameters.
out = bwferet(CC,properties)CC.
out = bwferet(L,properties)L.
Examples
Input Arguments
Output Arguments
Algorithms
The Feret properties of an object are measured by using boundary points on the antipodal vertices of the convex hull that encloses that object.
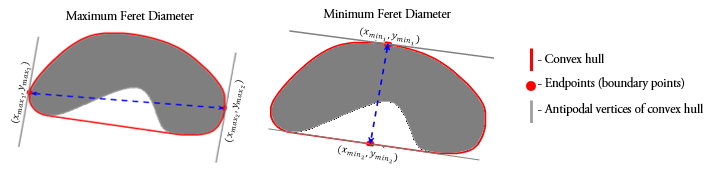
Given the endpoint coordinates of the maximum (or minimum) Feret diameter, , the maximum (or minimum) Feret angle is measured as .
Extended Capabilities
Version History
Introduced in R2019aSee Also
bwconncomp | bwlabel | bwlabeln | labelmatrix | regionprops

