unscentedKalmanFilter
Create unscented Kalman filter object for online state estimation
Description
unscentedKalmanFilter creates an object for online state
estimation of a discrete-time nonlinear system using the discrete-time unscented Kalman filter
algorithm.
When you perform online state estimation, you first create the nonlinear state transition
function f and measurement function h. You then
construct the unscentedKalmanFilter object using these nonlinear
functions, and specify whether the noise terms are additive or nonadditive.
After you create the object, you use the predict
command to predict state estimates at the next time step, and correct to
correct state estimates using the unscented Kalman filter algorithm and real-time data. For
information about the algorithm, see Algorithms.
Creation
Syntax
Description
obj = unscentedKalmanFilter(stateTransitionFcn,measurementFcn,initialState)
stateTransitionFcnis a function that calculates the state of the system at time k, given the state vector at time k-1. This function is stored in theStateTransitionFcnproperty of the object.measurementFcnis a function that calculates the output measurement of the system at time k, given the state at time k. This function is stored in theMeasurementFcnproperty of the object.initialStatespecifies the initial value of the state estimates. This value is stored in theStateproperty of the object.
After creating the object, use the correct and predict functions to update state estimates and state
estimation error covariance values using a discrete-time unscented Kalman filter
algorithm and real-time data.
predictupdatesobj.Stateandobj.StateCovariancewith the predicted value at time step k using the state value at time step k–1.correctupdatesobj.Stateandobj.StateCovariancewith the estimated values at time step k using measured data at time step k.
obj = unscentedKalmanFilter(___,Name,Value)[1;0], to specify
these values after creation, use obj.State = [1;0].
Properties
Object Functions
correct | Correct state and state estimation error covariance using extended or unscented Kalman filter, or particle filter and measurements |
predict | Predict state and state estimation error covariance at next time step using extended or unscented Kalman filter, or particle filter |
residual | Return measurement residual and residual covariance when using extended or unscented Kalman filter |
clone | Copy online state estimation object |
Examples
Algorithms
The discrete-time unscented Kalman filter algorithm performs online state estimation of a discrete-time nonlinear system.
Consider a plant with states x, input u, output y, process noise w, and measurement noise v. Assume that you can represent the plant as a nonlinear system.
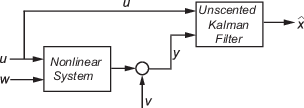
The algorithm computes the state estimates of the nonlinear system using state transition and measurement functions specified by you. The software lets you specify the noise in these functions as additive or nonadditive:
Additive Noise Terms — The state transition and measurements equations have the following form:
Here f is a nonlinear state transition function that describes the evolution of states
xfrom one time step to the next. The nonlinear measurement function h relatesxto the measurementsyat time stepk.wandvare the zero-mean, uncorrelated process and measurement noises, respectively. These functions can also have additional input arguments that are denoted byusandumin the equations. For example, the additional arguments could be time stepkor the inputsuto the nonlinear system. There can be multiple such arguments.Note that the noise terms in both equations are additive. That is,
x(k)is linearly related to the process noisew(k-1), andy(k)is linearly related to the measurement noisev(k).Nonadditive Noise Terms — The software also supports more complex state transition and measurement functions where the state x[k] and measurement y[k] are nonlinear functions of the process noise and measurement noise, respectively. When the noise terms are nonadditive, the state transition and measurements equation have the following form:
When you perform online state estimation, you first create the nonlinear state transition
function f and measurement function h. You then
construct the unscentedKalmanFilter object using these nonlinear
functions and specify whether the noise terms are additive or nonadditive.
After you create the object, you use the predict
command to predict state estimates at the next time step, and correct to
correct state estimates using the unscented Kalman filter algorithm and real-time data. For
additional details about the algorithm, see Extended and Unscented Kalman Filter Algorithms for Online State Estimation.
Extended Capabilities
Version History
Introduced in R2016bSee Also
Functions
predict|correct|residual|clone|extendedKalmanFilter
Blocks
Topics
- Nonlinear State Estimation Using Unscented Kalman Filter and Particle Filter
- Generate Code for Online State Estimation in MATLAB
- What Is Online Estimation?
- Extended and Unscented Kalman Filter Algorithms for Online State Estimation
- Validate Online State Estimation at the Command Line
- Troubleshoot Online State Estimation