Thermostatic Expansion Valve (2P)
Flow control valve that maintains evaporator superheat
Libraries:
Simscape /
Fluids /
Two-Phase Fluid /
Valves & Orifices /
Flow Control Valves
Description
The Thermostatic Expansion Valve (2P) block models a valve with a pressure drop that maintains an evaporator superheat in a two-phase fluid network. You typically place this valve between a condenser and an evaporator in a refrigeration system to maintain a specific temperature differential by moderating the flow into the evaporator.
The valve behavior depends on the superheat, which is the difference in temperature between the vapor at the evaporator outlet and the fluid evaporating temperature. The valve opens if the superheat increases to let more flow through, and the valve closes if the superheat decreases to let less flow through. When the superheat drops to or below the value of the Static (minimum) evaporator superheat parameter, then the valve is fully closed. The closed valve reduces the flow through the evaporator, which reduces the heat transfer and increases the outlet temperature. When you use the MOP limit parameter to enable a maximum pressure or temperature limit, the valve closes when the temperature or pressure exceeds the limit.
The bulb sensor at port S measures the evaporator outlet temperature.
If you set the Pressure equalization parameter to
External pressure equalization, the block uses data from
the evaporator at port E for internal pressure equalization.
Otherwise, the block uses the pressure at port B for internal
pressure equalization. The block balances the bulb pressure, which acts to open the
valve, with the valve equalization pressure, which acts to close the valve.
Analytical Parameterization
When you set Valve parameterization to Nominal capacity,
superheat, and operating conditions, the block uses an analytical
model. In this setting, the block fits the analytical model to the performance data
so that when the refrigeration system operates at the specified nominal evaporating
temperature, condensing temperature, and condenser subcooling, the block meters
enough flow into the evaporator to maintain the evaporator superheat while the block
transfers heat at the evaporator capacity. Subcooling is the difference in
temperature between the condenser outlet and the condensing temperature.
For this parameterization, the block assumes a straight-charged bulb and assumes that the
sensing bulb contains the same fluid as the refrigerant. To model a cross-charged
bulb, set Valve parameterization to Tabulated data
- quadrant diagram.
The valve operates to control the mass flow rate between a condenser and an evaporator by regulating the effective opening area, Seff. The mass flow rate is
where:
vin is the inlet specific volume, or the fluid volume per unit mass.
Δp is the pressure differential over the valve, pA – pB.
Δplam is the pressure threshold for transitional flow. Below this value, the flow is laminar
where Blam is the value of the Laminar flow pressure ratio parameter.
The effective valve area depends on the pressure difference between the measured pressure, pbulb and the equalization pressure, peq
where:
β is a valve constant determined from the nominal operating conditions. See Determining β from Nominal Conditions.
Tevap is the evaporating temperature.
When Nominal pressure specification is
Pressure at specified saturation temperature, Tevap is the value of the Nominal evaporating (saturation) temperature parameter.When Nominal pressure specification is
Specified pressure, Tevap is the saturation temperature that corresponds to the value of the Nominal evaporator outlet pressure parameter.ΔTstatic is the Static (minimum) evaporator superheat parameter.
psat(Tevap) is the fluid saturation pressure as a function of Tevap. The block uses the
tablelookupfunction to identify this value.psat(Tevap+ΔTstatic) is the saturation pressure as a function of Tevap+ΔTstatic. The block uses the
tablelookupfunction to identify this value.pbulb is the fluid pressure of the bulb. The bulb pressure is the saturation pressure, , unless you set MOP limit to
On - Specify maximum operating pressureand the pressure reaches the maximum pressure. See Maximum Outlet Pressure Limit for more information. Tbulb is the bulb fluid temperature.peq depends on the valve pressure equalization setting:
When you set Pressure equalization to
Internal pressure equalization, peq is the pressure at port B.When you set Pressure equalization to
External pressure equalization, peq is the pressure at port E.
The effective valve area has limits. The minimum effective valve area, Seff,min, is
where fleak is the value of the Closed valve leakage as a fraction of nominal flow parameter. To see how the block calculates the nominal effective valve area, Seff,nom and maximum effective valve area, see Determining β from Nominal Conditions.
β represents the relationship between the nominal evaporator superheat and the nominal evaporator capacity, the rate of heat transfer between the two fluids in the evaporator:
where psat(Tevap+ΔTnom) is the saturation pressure at the sum of the evaporator outlet temperature and the Nominal (static + opening) evaporator superheat parameter.
The block calculates the nominal effective valve area,
Seff,nom, as a function of the
nominal condenser and evaporator thermodynamics. When Capacity
specification is Evaporator heat
transfer, the nominal effective valve area is
When Capacity specification is Mass flow
rate, the nominal effective valve area is
where:
Tcond is the condensing saturation temperature.
When Nominal pressure specification is
Pressure at specified saturation temperature, Tcond is the value of the Nominal condensing (saturation) temperature parameter.When Nominal pressure specification is
Specified pressure, Tcond is the saturation temperature that corresponds to the value of the Nominal condenser outlet pressure parameter.vcond is the liquid specific volume at Tcond.
Qnom is the Nominal evaporator heat transfer parameter.
cp,evap is the vapor specific heat at Tevap.
hevap is the vapor specific enthalpy at Tevap.
cp,cond is the liquid specific heat at Tcond.
hcond is the liquid specific enthalpy at Tcond.
ΔTsub is the Nominal condenser subcooling parameter.
is the Nominal mass flow rate parameter.
When Capacity specification is
Evaporator heat transfer, the block determines
the maximum effective area of the valve in the same way as
Seff,nom, but uses the value
of Maximum evaporator heat transfer parameter instead of
the Nominal evaporator heat transfer parameter. When
Capacity specification is Mass flow
rate, the block uses the value of the Maximum mass
flow rate parameter instead of the Nominal mass flow
rate parameter.
You can limit the maximum outlet pressure (MOP) in the evaporator by setting the
MOP limit parameter to On - Specify
maximum operating pressure or On - Specify
maximum operating temperature. When you use one of these
settings, the valve closes when the bulb temperature or pressure exceeds the
temperature or pressure associated with maximum bulb pressure, and opens once
the pressure reduces. If you set MOP limit to
Off, or the measured pressure is below the limit, . Otherwise, when the measurement exceeds the limit, the bulb
pressure remains at
where:
pbulb,MOP is a function of the Maximum evaporator outlet pressure parameter, peq,MOP, or the pressure specified by the Maximum evaporating (saturation) temperature parameter, and the nominal evaporator temperature:
Tbulb is the bulb fluid temperature. This value is the temperature at port S if you clear the Bulb temperature dynamics check box. The block applies a first-order delay to the bulb temperature if you select Bulb temperature dynamics.
Tbulb,MOP is the associated temperature at the pressure pbulb,MOP.
Four-Quadrant Diagram
To visualize the four-quadrant diagram, right-click the block and select Fluids > Plot 4-Quadrant Diagram.
When Valve parameterization is Tabulated data - quadrant
diagram, the block uses user-provided data to plot in all
quadrants. See Tabulated Data Parameterization.
When Valve parameterization is Nominal capacity,
superheat, and operating conditions, the block calculates the data
in all quadrants by using the analytical valve model, described in Analytical Parameterization. Because the
analytical model assumes a straight-charged bulb, the diagram plots the two curves
in quadrant 1 on top of each other.
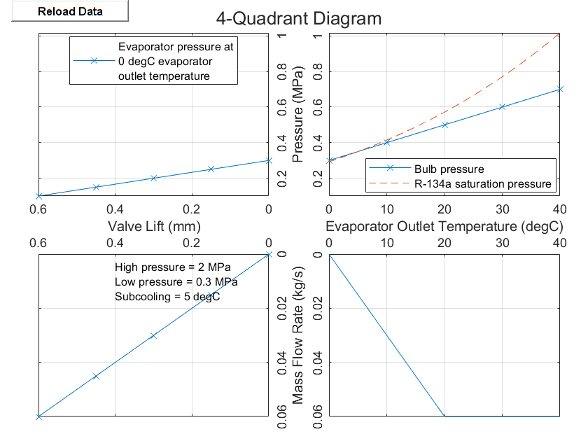
The diagram shows the four quadrants:
Quadrant 1: Plot of the fluid pressure of the sensing bulb versus the evaporator outlet temperature when the sensing bulb is attached to the evaporator outlet. In this image, the graph includes a second line that represents the vapor saturation curve of the refrigerant in the cycle, which is a plot of saturation pressure versus saturation temperature.
Quadrant 2: Plot of the valve lift versus the evaporator outlet pressure. The valve lift is the position of the needle of the valve. As the evaporator outlet pressure decreases, the valve opens and valve lift increases.
When Valve parameterization is
Tabulated data - quadrant diagram, the plot holds the evaporator outlet temperature constant at the Reference evaporator outlet temperature parameter value.Quadrant 3: Plot of the mass flow rate through the valve versus valve lift.
When Valve parameterization is
Tabulated data - quadrant diagram, the plot holds the inlet pressure of the valve constant at the Reference condenser outlet pressure parameter, the inlet temperature constant at the Reference condenser subcooling parameter, and the outlet pressure constant at the Reference evaporator outlet pressure parameter.Quadrant 4: Plot of the mass flow rate through the valve versus evaporator outlet temperature.
When Valve parameterization is
Tabulated data - quadrant diagram, the plot holds the inlet pressure of the valve constant at the Reference condenser outlet pressure parameter, the inlet temperature constant at the Reference condenser subcooling parameter, and the outlet pressure constant at the Reference evaporator outlet pressure parameter.
Tabulated Data Parameterization
When you set Valve parameterization to Tabulated data -
quadrant diagram, the block uses tabulated data. Three of the four
curves in the thermostatic expansion valve quadrant diagram specify the valve
characteristics. The supplier typically provides this diagram.
To determine block characteristics, the block performs interpolation on the data you provide in the parameters Quadrant 1 - Evaporator outlet temperature vector, Quadrant 1 - Bulb pressure vector, Quadrant 2 - Valve lift vector, Quadrant 2 - Evaporator outlet pressure vector, Quadrant 3 - Valve lift vector, and Quadrant 3 - Mass flow rate vector.
The block determines the mass flow rate through the valve from the inlet pressure, outlet pressure, equalization pressure, and sensing bulb temperature by using the data from quadrant 1 to quadrant 3 and a series of interpolations. The block first calculates the quadrant 2 evaporator outlet pressure as
where:
peq depends on the valve pressure equalization setting:
When you set Pressure equalization to
Internal pressure equalization, peq is the pressure at port B.When you set Pressure equalization to
External pressure equalization, peq is the pressure at port E.
pbulb(Tbulb) is the bulb fluid pressure interpolated at the bulb fluid temperature Tbulb. You specify the bulb fluid pressure data in the parameter Quadrant 1 – Bulb pressure vector.
pbulb(Tevap,ref) is the bulb fluid pressure interpolated at the reference evaporator outlet temperature Tevap,ref.
The block uses the valve lift data, L, from the Quadrant 2 – Valve lift vector parameter to interpolate the valve lift at the values in Quadrant 2 – Evaporator outlet pressure vector, which gives L = L(pevap,Q2). The block then uses the reference mass flow rate, , from the Quadrant 3 – Mass flow rate vector, to interpolate the mass flow rate at the valve lift values . The block scales the reference mass flow rate to the actual mass flow rate with
where:
pcond,ref is the Reference condenser outlet pressure parameter.
pevap,ref is the Reference evaporator outlet pressure parameter.
vref is the specific volume that corresponds to the Reference condenser outlet pressure and Reference condenser subcooling parameters.
vin is the inlet specific volume, or the fluid volume per unit mass.
Δp is the pressure differential over the valve, pA – pB.
Δplam is the pressure threshold for transitional flow. Below this value, the flow is laminar. The block calculates this value as:
where Blam is the value of the Laminar flow pressure ratio parameter.
Pressure Equalization
The equalization pressure is the pressure at the evaporator outlet that governs valve operability. In physical systems with low pressure loss in the evaporator due to viscous friction, pressure equalization can occur internally with the pressure at port B. This is internal pressure equalization. In systems with larger losses, connect the evaporator outlet port to the valve block at port E.
Bulb Temperature Dynamics
You can model the bulb dynamic response to changing temperatures by selecting Bulb temperature dynamics. This introduces a first-degree lag in the measured temperature
where:
TS is the temperature at port S. If you do not model bulb dynamics, this value is Tbulb.
τbulb is the value of the Bulb thermal time constant parameter.
Fluid Specific Volume Dynamics
When the fluid at the valve inlet is a liquid-vapor mixture, the block calculates the specific volume as
where:
xdyn is the inlet vapor quality. The block applies a first-order lag to the inlet vapor quality of the mixture.
vliq is the liquid specific volume of the fluid.
vvap is the vapor specific volume of the fluid.
If the inlet fluid is liquid or vapor, vin is the respective liquid or vapor specific volume.
If the inlet vapor quality is a liquid-vapor mixture, the block applies a first-order time lag
where:
xdyn is the dynamic vapor quality.
xin is the current inlet vapor quality.
τ is the value of the Inlet phase change time constant parameter.
If the inlet fluid is a subcooled liquid, xdyn is equal to xin.
Conservation Equations
Mass is conserved through the valve
where:
is the mass flow rate at port A.
is the mass flow rate at port B.
The block supports reversed flows numerically, however, the valve block is not designed for flows from port B to port A.
The block conserves energy flow through the valve
where:
ΦA is the energy flow rate at port A.
ΦB is the energy flow rate at port B.
Examples
Ports
Conserving
Parameters
References
[1] Eames, Ian W., Adriano Milazzo, and Graeme G. Maidment. "Modelling Thermostatic Expansion Valves." International Journal of Refrigeration 38 (February 2014): 189-97.


