Pressure-Compensated 3-Way Flow Control Valve
(To be removed) Hydraulic pressure compensating 3-way valve
The Hydraulics (Isothermal) library will be removed in a future release. Use the Isothermal Liquid library instead.
For more information on updating your models, see Upgrading Hydraulic Models to Use Isothermal Liquid Blocks.
Library
Flow Control Valves
Description
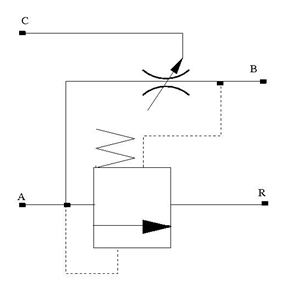
The Pressure-Compensated 3-Way Flow Control Valve block represents a 3-way pressure-compensated flow control valve as a data-sheet-based model. The valve model includes a variable orifice and a normally closed pressure-control valve, connected in parallel with the orifice. The purpose of the pressure-control valve is to maintain a preset pressure differential across the orifice by diverting some flow from port A to the tank (port R) if the pressure differential exceeds the preset value. Port C controls the orifice opening, as shown in the following figure.
Depending on data listed in the manufacturer's catalogs or data sheets for your particular valve, you can choose one of the following model parameterization options:
By maximum area and opening— Use this option if the data sheet provides only the orifice maximum area and the control member maximum stroke.By area vs. opening table— Use this option if the catalog or data sheet provides a table of the orifice passage area based on the control member displacementA=A(h).
In the first case, the passage area is assumed to be linearly dependent on the control
member displacement, that is, the orifice is assumed to be closed if the initial orifice
opening is set to zero and the control member position also equals zero. The maximum
orifice opening takes place at the maximum displacement. In the second case, the passage
area is determined by one-dimensional interpolation from the table
A=A(h).
The pressure-control valve representation does not account for inertia, friction, or hydraulic forces. The valve has the following area-pressure differential relationship:
where
| Apc | Pressure-control valve passage area |
| p | Pressure differential across the orifice |
| pset | Preset pressure differential |
| preg | Regulation range |
| Amax_pc | Pressure-control valve maximum area |
| Aleak | Closed orifice leakage area for pressure compensator |
Both for the variable orifice and the pressure compensator, a small leakage area is assumed to exist even after the orifice is completely closed. Physically, it represents a possible clearance in the closed valve, but the main purpose of the parameter is to maintain numerical integrity of the circuit by preventing a portion of the system from getting isolated after the valve is completely closed. An isolated or “hanging” part of the system could affect computational efficiency and even cause failure of computation.
After the area has been determined, the block computes the flow rate for both the orifice and the pressure compensator according to the following equations:
h = x0 + x
where
| q | Flow rate |
| p | Pressure differential |
| pA, pB, pR | Gauge pressures at the block terminals |
| CD | Flow discharge coefficient |
| A | Instantaneous orifice passage area |
| Amax | Orifice maximum area |
| Aleak | Closed orifice leakage area |
| hmax | Control member maximum displacement |
| x0 | Initial opening |
| x | Control member displacement from initial position |
| h | Orifice opening |
| ρ | Fluid density |
| ν | Fluid kinematic viscosity |
| pcr | Minimum pressure for turbulent flow |
| Recr | Critical Reynolds number |
| DH | Instantaneous orifice hydraulic diameter |
Connections A, B, and R are the conserving hydraulic ports associated with the valve inlet, outlet, and return, respectively. Connection C is a physical signal port through which the orifice opening is controlled. The block positive direction is from port A to port B. Positive signal at port C opens the valve.
Assumptions and Limitations
Fluid inertia and pressure compensator loading are not taken into account.
Parameters
Variable Orifice Tab
- Orifice parameterization
Select one of the following methods for specifying the orifice:
By maximum opening and area— Provide values for the maximum orifice area and the maximum orifice opening. The passage area is linearly dependent on the control member displacement, that is, the orifice is closed at the initial position of the control member (zero displacement), and the maximum opening takes place at the maximum displacement. This is the default method.By orifice area vs. orifice opening table— Provide tabulated data of orifice openings and corresponding orifice areas. The passage area is determined by one-dimensional table lookup. You have a choice of two interpolation methods and two extrapolation methods.
- Orifice maximum area
The area of a fully opened orifice. The parameter value must be greater than zero. The default value is
1e-4m^2. This parameter is used if Orifice parameterization is set toBy maximum opening and area.- Orifice maximum opening
The maximum displacement of the control member. The parameter value must be greater than zero. The default value is
0.005m. This parameter is used if Orifice parameterization is set toBy maximum opening and area.- Tabulated orifice openings
Vector of input values for orifice openings, specified as a one-dimensional array. The input values vector must be strictly increasing. The values can be nonuniformly spaced. The minimum number of values depends on the interpolation method: you must provide at least two values for linear interpolation, at least three values for smooth interpolation. The default values, in mm, are
[-6, 0, 1, 3, 6, 9, 15]. This parameter is used if Orifice parameterization is set toBy orifice area vs. orifice opening table. Tabulated orifice openings values will be used together with Tabulated orifice area values for one-dimensional table lookup.- Tabulated orifice area
Vector of orifice areas, specified as a one-dimensional array. The vector must be the same size as the orifice openings vector. All the values must be positive. The default values, in cm^2, are
[1e-7, 1e-6, 0.08, 0.145, 0.96, 1, 1.001]. This parameter is used if Orifice parameterization is set toBy orifice area vs. orifice opening table.- Interpolation method
This parameter is used if Orifice parameterization is set to
By orifice area vs. orifice opening table. Select one of the following interpolation methods for approximating the output value when the input value is between two consecutive grid points:Linear— Select this option to get the best performance.Smooth— Select this option to produce a continuous curve with continuous first-order derivatives.
For more information on interpolation algorithms, see the PS Lookup Table (1D) block reference page.
- Extrapolation method
This parameter is used if Orifice parameterization is set to
By orifice area vs. orifice opening table. Select one of the following extrapolation methods for determining the output value when the input value is outside the range specified in the argument list:Linear— Select this option to produce a curve with continuous first-order derivatives in the extrapolation region and at the boundary with the interpolation region.Nearest— Select this option to produce an extrapolation that does not go above the highest point in the data or below the lowest point in the data.
For more information on extrapolation algorithms, see the PS Lookup Table (1D) block reference page.
- Orifice initial opening
Orifice initial opening. The parameter can be positive (underlapped orifice), negative (overlapped orifice), or 0 for zero-lap configuration. The default value is
0.- Orifice flow discharge coefficient
Semi-empirical coefficient that is used in the computation of flow rate through the orifice. Its value depends on the geometrical properties of the orifice and usually is provided in textbooks or manufacturer data sheets. The default value is
0.6.- Orifice laminar transition specification
Select how the block transitions between the laminar and turbulent regimes:
Pressure ratio— The transition from laminar to turbulent regime is smooth and depends on the value of the Orifice laminar flow pressure ratio parameter. This method provides better simulation robustness.Reynolds number— The transition from laminar to turbulent regime is assumed to take place when the Reynolds number reaches the value specified by the Orifice critical Reynolds number parameter.
- Orifice laminar flow pressure ratio
Pressure ratio at which the flow transitions between laminar and turbulent regimes. The default value is
0.999. This parameter is visible only if the Orifice laminar transition specification parameter is set toPressure ratio.- Orifice critical Reynolds number
The maximum Reynolds number for laminar flow. The value of the parameter depends on the orifice geometrical profile. You can find recommendations on the parameter value in hydraulics textbooks. The default value is
12. This parameter is visible only if the Orifice laminar transition specification parameter is set toReynolds number.- Orifice leakage area
The total area of possible leaks in the completely closed orifice. The main purpose of the parameter is to maintain numerical integrity of the circuit by preventing a portion of the system from getting isolated after the valve is completely closed. The parameter value must be greater than 0. The default value is
1e-9m^2.
Pressure Compensator Tab
- Pressure differential across orifice setting
Pressure difference that must be maintained across the variable orifice by the pressure compensator. The default value is
6e5Pa.- Pressure differential regulation range
Pressure increase over the preset level needed to fully open the pressure compensator orifice. The lower the value of the range, the higher the valve sensitivity. The default value is
0.5e5Pa.- Pressure compensator maximum area
The area of a fully opened pressure compensator. The parameter value must be greater than zero. The default value is
1e-4m^2.- Pressure compensator flow discharge coefficient
Semi-empirical coefficient that is used in the computation of flow rate through the pressure compensator. The default value is
0.6.- Pressure compensator laminar transition specification
Select how the block transitions between the laminar and turbulent regimes:
Pressure ratio— The transition from laminar to turbulent regime is smooth and depends on the value of the Pressure compensator laminar flow pressure ratio parameter. This method provides better simulation robustness.Reynolds number— The transition from laminar to turbulent regime is assumed to take place when the Reynolds number reaches the value specified by the Pressure compensator critical Reynolds number parameter.
- Pressure compensator laminar flow pressure ratio
Pressure ratio at which the flow transitions between laminar and turbulent regimes. The default value is
0.999. This parameter is visible only if the Pressure compensator laminar transition specification parameter is set toPressure ratio.- Pressure compensator critical Reynolds number
The maximum Reynolds number for laminar flow. The value of the parameter depends on the orifice geometrical profile. You can find recommendations on the parameter value in hydraulics textbooks. The default value is
12. This parameter is visible only if the Pressure compensator laminar transition specification parameter is set toReynolds number.- Pressure compensator leakage area
The total area of possible leaks in the completely closed orifice. Must be greater than 0. The main purpose of the parameter is to maintain numerical integrity of the circuit by preventing a portion of the system from getting isolated after the valve is completely closed. The default value is
1e-9m^2.
Global Parameters
Parameters determined by the type of working fluid:
Fluid density
Fluid kinematic viscosity
Use the Hydraulic Fluid block or the Custom Hydraulic Fluid block to specify the fluid properties.
Ports
The block has the following ports:
AHydraulic conserving port associated with the valve inlet.
BHydraulic conserving port associated with the valve outlet.
RHydraulic conserving port that connects with the tank.
CPhysical signal control port.

