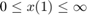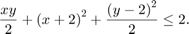Algorithm | Algorithm used by patternsearch. The
Algorithm setting affects the available options.
For algorithm details, see How Pattern Search Polling Works and Nonuniform Pattern Search (NUPS) Algorithm. For examples of algorithm effects, see Explore patternsearch Algorithms and
Explore patternsearch Algorithms in Optimize Live Editor Task. | {"classic"} | "nups" |
"nups-gps" | "nups-mads" |
| Cache | With Cache set to "on",
patternsearch keeps a history of the mesh
points it polls. At subsequent iterations,
patternsearch does not poll points close to
those already polled. Use this option if
patternsearch runs slowly while computing the
objective function. If the objective function is stochastic, do not use
this option. Note Cache does not work when you run the solver in parallel.
| "on" | {"off"}
|
| CacheSize | Size of the history. | Nonnegative scalar | {1e4} |
| CacheTol | Largest distance from the current mesh point to any point in the
history in order for patternsearch to avoid polling
the current point. Use if the Cache option is set to
"on". | Nonnegative scalar | {eps} |
ConstraintTolerance
| Tolerance on constraints. For an options structure, use TolCon. | Positive scalar | {1e-6} |
Display
| Level of display, meaning how much information patternsearch returns
to the Command Line during the solution process. | "off" | "iter" | "diagnose" |
{"final"} |
FunctionTolerance | Tolerance on the function. Iterations stop if the change in
function value is less than FunctionTolerance and the
mesh size is less than StepTolerance. This option
does not apply to MADS (mesh adaptive direct search)
polling. For an options structure, use
TolFun. | Nonnegative scalar | {1e-6} |
InitialMeshSize | Initial mesh size for the algorithm. See How Pattern Search Polling Works. | Positive scalar | {1.0} |
| InitialPenalty | Initial value of the penalty parameter. See Nonlinear Constraint Solver Algorithm for Pattern Search. | Positive scalar | {10} |
MaxFunctionEvaluations
| Maximum number of objective function evaluations. For an options structure, use MaxFunEvals. | Nonnegative integer | {"2000*numberOfVariables"}, where
numberOfVariables is the number of problem
variables |
MaxIterations
| Maximum number of iterations. For an options structure, use MaxIter. | Nonnegative integer | {"100*numberOfVariables"}, where
numberOfVariables is the number of problem
variables |
| MaxMeshSize | Maximum mesh size used in a poll or search step. See How Pattern Search Polling Works. | Nonnegative scalar | {Inf} |
MaxTime
| Total time (in seconds) allowed for optimization. For an options structure, use TimeLimit. | Nonnegative scalar | {Inf} |
MeshContractionFactor | Mesh contraction factor for an unsuccessful
iteration. This option applies only when Algorithm is
"classic". For an options structure, use
MeshContraction. | Positive scalar | {0.5} |
MeshExpansionFactor | Mesh expansion factor for a successful iteration. This option applies only when Algorithm is
"classic". For an options structure, use
MeshExpansion. | Positive scalar | {2.0} |
| MeshRotate | Flag to rotate the pattern before declaring a point to be optimum.
See Mesh Options. This option applies only when Algorithm is
"classic". | "off" | {"on"}
|
MeshTolerance
| Tolerance on the mesh size. For an options structure, use
TolMesh. | Nonnegative scalar | {1e-6} |
OutputFcn
| Function called by an optimization function at each iteration. Specify as a function
handle or a cell array of function handles. For an options
structure, use OutputFcns. | Function handle or cell array of function handles | {[]} |
| PenaltyFactor | Penalty update parameter. See Nonlinear Constraint Solver Algorithm for Pattern Search. | Positive scalar | {100} |
PlotFcn
| Plots of output from the pattern search. Specify as the name of a built-in plot
function, a function handle, or a cell array of names of built-in plot
functions or function handles. For an options structure, use
PlotFcns. | {[]} | "psplotbestf" |
"psplotfuncount" |
"psplotmeshsize" |
"psplotbestx" |
"psplotmaxconstr" | custom plot function
|
| PlotInterval | Number of iterations for plots. 1 means plot
every iteration, 2 means plot every other iteration,
and so on. | positive integer | {1} |
PollMethod
| Polling strategy used in the pattern search. This option applies only when Algorithm is
"classic". Note You cannot use MADS polling when the problem has linear equality constraints. | {"GPSPositiveBasis2N"}
|
"GPSPositiveBasisNp1" |
"GSSPositiveBasis2N" |
"GSSPositiveBasisNp1" |
"MADSPositiveBasis2N" |
"MADSPositiveBasisNp1"
|
PollOrderAlgorithm | Order of the poll directions in the pattern
search. This option applies only when Algorithm is
"classic". For an options structure, use
PollingOrder. | "Random" | "Success" |
{"Consecutive"}
|
ScaleMesh | Automatic scaling of variables. For an options
structure, use ScaleMesh = "on" or
"off". | {true}| false
|
SearchFcn | Type of search used in the pattern search. Specify as a name or a
function handle. For an options structure, use
SearchMethod. | "GPSPositiveBasis2N" | "GPSPositiveBasisNp1" |
"GSSPositiveBasis2N" | "GSSPositiveBasisNp1" | "MADSPositiveBasis2N"
| "MADSPositiveBasisNp1" | "searchga" | "searchlhs" |
"searchneldermead" | "rbfsurrogate" | {[]} | custom search
function
|
StepTolerance | Tolerance on the variable. Iterations stop if both the change in
position and the mesh size are less than
StepTolerance. This option does not apply to MADS
polling. For an options structure, use
TolX. | Nonnegative scalar | {1e-6} |
| TolBind | Binding tolerance. See Constraint Parameters. | Nonnegative scalar | {1e-3} |
UseCompletePoll | Flag to complete the poll around the current point. See How Pattern Search Polling Works. This option applies only when Algorithm is
"classic". Note For the "classic" algorithm, you must set
UseCompletePoll to true
for vectorized or parallel polling. Similarly, set
UseCompleteSearch to true
for vectorized or parallel searching. Beginning in R2019a, when you set the
UseParallel option to true,
patternsearch internally overrides the
UseCompletePoll setting to true so that the function
polls in parallel. For an options structure, use CompletePoll =
"on" or "off". | true | {false}
|
UseCompleteSearch | Flag to complete the search around the current point when the
search method is a poll method. See Searching and Polling. This option applies only when Algorithm is
"classic". Note For the "classic" algorithm, you must set
UseCompleteSearch to true
for vectorized or parallel searching. For an options structure, use CompleteSearch
= "on" or "off". | true | {false}
|
UseParallel
| Flag to compute objective and nonlinear constraint functions in parallel. See Vectorized and Parallel Options
and How to Use Parallel Processing in Global Optimization Toolbox. Note For the "classic" algorithm, you must set
UseCompletePoll to true
for vectorized or parallel polling. Similarly, set
UseCompleteSearch to true
for vectorized or parallel searching. Beginning in R2019a, when you set the
UseParallel option to true,
patternsearch internally overrides the
UseCompletePoll setting to true so that the function
polls in parallel. Note Cache does not work when you run the solver in parallel.
| true | {false}
|
UseVectorized
| Specifies whether functions are vectorized. See Vectorized and Parallel Options
and Vectorize the Objective and Constraint Functions. Note For the "classic" algorithm, you must set
UseCompletePoll to true
for vectorized or parallel polling. Similarly, set
UseCompleteSearch to true
for vectorized or parallel searching. For an options structure, use Vectorized =
"on" or "off". | true | {false}
|