forecast
Forecast vector error-correction (VEC) model responses
Syntax
Description
Conditional and Unconditional Forecasts for Numeric Arrays
Y = forecast(Mdl,numperiods,Y0)Y over a length
numperiods forecast horizon, using the fully specified
VEC(p – 1) model Mdl. The forecasted
responses represent the continuation of the presample data in the numeric array
Y0.
Y = forecast(Mdl,numperiods,Y0,Name=Value)forecast returns numeric arrays when all optional
input data are numeric arrays. For example,
forecast(Mdl,10,Y0,X=Exo) returns a numeric array
containing a 10-period forecasted response path from Mdl
and the numeric matrix of presample response data Y0, and
specifies the numeric matrix of future predictor data for the model regression
component in the forecast horizon Exo.
To produce a conditional forecast, specify future response data in a numeric
array by using the YF name-value argument.
Unconditional Forecasts for Tables and Timetables
Tbl2 = forecast(Mdl,numperiods,Tbl1)Tbl2 containing the length
numperiods paths of multivariate MMSE response variable
forecasts, which result from computing unconditional forecasts from the VEC
model Mdl. forecast uses the table
or timetable of presample data Tbl1 to initialize the
response series. (since R2022b)
forecast selects the variables in
Mdl.SeriesNames to forecast, or it selects all variables
in Tbl1. To select different response variables in
Tbl1 to forecast, use the
PresampleResponseVariables name-value argument.
Tbl2 = forecast(Mdl,numperiods,Tbl1,Name=Value)forecast(Mdl,10,Tbl1,PresampleResponseVariables=["GDP"
"CPI"]) returns a timetable of response variables containing their
unconditional forecasts from the VEC model Mdl, initialized
by the data in the GDP and CPI variables
of the timetable of presample data in Tbl1. (since R2022b)
Conditional Forecasts for Tables and Timetables
Tbl2 = forecast(Mdl,numperiods,Tbl1,InSample=InSample,ResponseVariables=ResponseVariables)Tbl2 containing the length
numperiods paths of multivariate MMSE response variable
forecasts and corresponding forecast MSEs, which result from computing
conditional forecasts from the VEC model Mdl.
forecast uses the table or timetable of presample
data Tbl1 to initialize the response series.
InSample is a table or timetable of future data in the
forecast horizon that forecast uses to compute
conditional forecasts and ResponseVariables specifies the
response variables in InSample. (since R2022b)
Tbl2 = forecast(Mdl,numperiods,Tbl1,InSample=InSample,ResponseVariables=ResponseVariables,Name=Value)
Examples
Consider a VEC model for the following seven macroeconomic series. Then, fit the model to the data and forecast responses 12 quarters into the future. Supply all required data in numeric matrices.
Gross domestic product (GDP)
GDP implicit price deflator
Paid compensation of employees
Nonfarm business sector hours of all persons
Effective federal funds rate
Personal consumption expenditures
Gross private domestic investment
Suppose that a cointegrating rank of 4 and one short-run term are appropriate, that is, consider a VEC(1) model.
Load the Data_USEconVECModel data set.
load Data_USEconVECModelFor more information on the data set and variables, enter Description at the command line.
Determine whether the data needs to be preprocessed by plotting the series on separate plots.
figure tiledlayout(2,2) nexttile plot(FRED.Time,FRED.GDP) title("Gross Domestic Product") ylabel("Index") xlabel("Date") nexttile plot(FRED.Time,FRED.GDPDEF) title("GDP Deflator") ylabel("Index") xlabel("Date") nexttile plot(FRED.Time,FRED.COE) title("Paid Compensation of Employees") ylabel("Billions of $") xlabel("Date") nexttile plot(FRED.Time,FRED.HOANBS) title("Nonfarm Business Sector Hours") ylabel("Index") xlabel("Date")
figure tiledlayout(2,2) nexttile plot(FRED.Time,FRED.FEDFUNDS) title("Federal Funds Rate") ylabel("Percent") xlabel("Date") nexttile plot(FRED.Time,FRED.PCEC) title("Consumption Expenditures") ylabel("Billions of $") xlabel("Date") nexttile plot(FRED.Time,FRED.GPDI) title("Gross Private Domestic Investment") ylabel("Billions of $") xlabel("Date")
Stabilize all series, except the federal funds rate, by applying the log transform. Scale the resulting series by 100 so that all series are on the same scale.
FRED.GDP = 100*log(FRED.GDP); FRED.GDPDEF = 100*log(FRED.GDPDEF); FRED.COE = 100*log(FRED.COE); FRED.HOANBS = 100*log(FRED.HOANBS); FRED.PCEC = 100*log(FRED.PCEC); FRED.GPDI = 100*log(FRED.GPDI);
Create a VEC(1) model using the shorthand syntax. Specify the variable names.
Mdl = vecm(7,4,1); Mdl.SeriesNames = FRED.Properties.VariableNames;
Mdl is a vecm model object. All properties containing NaN values correspond to parameters to be estimated given data.
Estimate the model using the entire data set and the default options.
EstMdl = estimate(Mdl,FRED.Variables)
EstMdl =
vecm with properties:
Description: "7-Dimensional Rank = 4 VEC(1) Model"
SeriesNames: "GDP" "GDPDEF" "COE" ... and 4 more
NumSeries: 7
Rank: 4
P: 2
Constant: [14.1329 8.77841 -7.20359 ... and 4 more]'
Adjustment: [7×4 matrix]
Cointegration: [7×4 matrix]
Impact: [7×7 matrix]
CointegrationConstant: [-28.6082 -109.555 77.0912 ... and 1 more]'
CointegrationTrend: [4×1 vector of zeros]
ShortRun: {7×7 matrix} at lag [1]
Trend: [7×1 vector of zeros]
Beta: [7×0 matrix]
Covariance: [7×7 matrix]
EstMdl is an estimated vecm model object. It is fully specified because all parameters have known values. By default, estimate imposes the constraints of the H1 Johansen VEC model form by removing the cointegrating trend and linear trend terms from the model. Parameter exclusion from estimation is equivalent to imposing equality constraints to zero.
Forecast responses from the estimated model over a three-year horizon. Specify the entire data set as presample observations.
numperiods = 12; Y0 = FRED.Variables; Y = forecast(EstMdl,numperiods,Y0);
Y is a 12-by-7 matrix of forecasted responses. Rows correspond to the forecast horizon, and columns correspond to the variables in EstMdl.SeriesNames.
Plot the forecasted responses and the last 50 true responses.
fh = dateshift(FRED.Time(end),"end","quarter",1:12); figure; tiledlayout(2,2) nexttile h1 = plot(FRED.Time((end-49):end),FRED.GDP((end-49):end)); hold on h2 = plot(fh,Y(:,1)); title("Gross Domestic Product"); ylabel("Index (scaled)"); xlabel("Date"); h = gca; fill([FRED.Time(end) fh([end end]) FRED.Time(end)],h.YLim([1 1 2 2]),"k", ... FaceAlpha=0.1,EdgeColor="none"); legend([h1 h2],"True","Forecast",Location="best") hold off nexttile h1 = plot(FRED.Time((end-49):end),FRED.GDPDEF((end-49):end)); hold on h2 = plot(fh,Y(:,2)); title("GDP Deflator"); ylabel("Index (scaled)"); xlabel("Date"); h = gca; fill([FRED.Time(end) fh([end end]) FRED.Time(end)],h.YLim([1 1 2 2]),"k", ... FaceAlpha=0.1,EdgeColor="none"); legend([h1 h2],"True","Forecast",Location="best") hold off nexttile h1 = plot(FRED.Time((end-49):end),FRED.COE((end-49):end)); hold on h2 = plot(fh,Y(:,3)); title("Paid Compensation of Employees"); ylabel("Billions of $ (scaled)"); xlabel("Date"); h = gca; fill([FRED.Time(end) fh([end end]) FRED.Time(end)],h.YLim([1 1 2 2]),"k", ... FaceAlpha=0.1,EdgeColor="none"); legend([h1 h2],"True","Forecast",Location="best") hold off nexttile h1 = plot(FRED.Time((end-49):end),FRED.HOANBS((end-49):end)); hold on h2 = plot(fh,Y(:,4)); title("Nonfarm Business Sector Hours"); ylabel("Index (scaled)"); xlabel("Date"); h = gca; fill([FRED.Time(end) fh([end end]) FRED.Time(end)],h.YLim([1 1 2 2]),"k", ... FaceAlpha=0.1,EdgeColor="none"); legend([h1 h2],"True","Forecast",Location="best") hold off
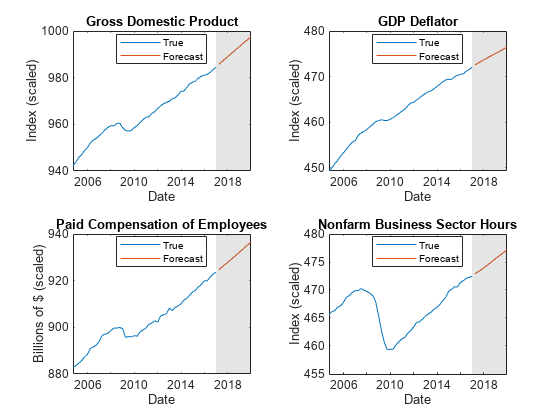
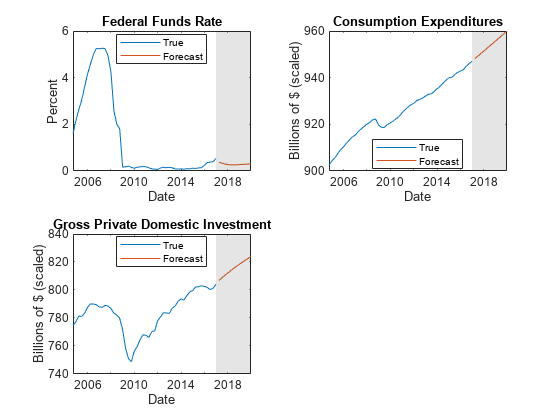
figure tiledlayout(2,2) nexttile h1 = plot(FRED.Time((end-49):end),FRED.FEDFUNDS((end-49):end)); hold on h2 = plot(fh,Y(:,5)); title("Federal Funds Rate"); ylabel("Percent"); xlabel("Date"); h = gca; fill([FRED.Time(end) fh([end end]) FRED.Time(end)],h.YLim([1 1 2 2]),"k", ... FaceAlpha=0.1,EdgeColor="none"); legend([h1 h2],"True","Forecast",Location="best") hold off nexttile h1 = plot(FRED.Time((end-49):end),FRED.PCEC((end-49):end)); hold on h2 = plot(fh,Y(:,6)); title("Consumption Expenditures"); ylabel("Billions of $ (scaled)"); xlabel("Date"); h = gca; fill([FRED.Time(end) fh([end end]) FRED.Time(end)],h.YLim([1 1 2 2]),"k", ... FaceAlpha=0.1,EdgeColor="none"); legend([h1 h2],"True","Forecast",Location="best") hold off nexttile h1 = plot(FRED.Time((end-49):end),FRED.GPDI((end-49):end)); hold on h2 = plot(fh,Y(:,7)); title("Gross Private Domestic Investment"); ylabel("Billions of $ (scaled)"); xlabel("Date"); h = gca; fill([FRED.Time(end) fh([end end]) FRED.Time(end)],h.YLim([1 1 2 2]),"k", ... FaceAlpha=0.1,EdgeColor="none"); legend([h1 h2],"True","Forecast",Location="best") hold off
This example is based on Return Matrix of VEC Model Forecasts. Forecast all response variables of the VEC model into a 3-year forecast horizon beyond the sampling data, given that the effective federal funds rate FEDFUNDS is 0.5% during each future quarter.
Load the Data_USEconVECModel data set.
load Data_USEconVECModelStabilize all series, except the federal funds rate, by applying the log transform. Scale the resulting series by 100 so that all series are on the same scale.
FRED.GDP = 100*log(FRED.GDP); FRED.GDPDEF = 100*log(FRED.GDPDEF); FRED.COE = 100*log(FRED.COE); FRED.HOANBS = 100*log(FRED.HOANBS); FRED.PCEC = 100*log(FRED.PCEC); FRED.GPDI = 100*log(FRED.GPDI);
Create a VEC(1) model using the shorthand syntax. Specify the variable names.
Mdl = vecm(7,4,1); Mdl.SeriesNames = FRED.Properties.VariableNames;
Estimate the model using the entire data set and the default options.
EstMdl = estimate(Mdl,FRED.Variables);
Suppose economists hypothesize that the effective federal funds rate will be at 0.5% for the next 12 quarters.
Create a matrix with the following qualities:
The matrix has 12 rows representing periods in the forecast horizon.
All columns associated with variables of
FRED, except forFEDFUNDS, are composed ofNaNvalues.The column corresponding to the variable
FEDFUNDSis composed of 0.5.
numperiods = 12;
CondF = NaN(numperiods,EstMdl.NumSeries);
idxFF = string(EstMdl.SeriesNames) == "FEDFUNDS";
CondF(:,idxFF) = 0.5*ones(numperiods,1);CondF is a 12-by-7 matrix of NaN values, except for the column associated with FEDFUNDS, which is a vector composed of the value 0.5. For each period in the forecast horizon, forecast fills the NaN elements of the matrix with forecasts, given the values of FEDFUNDS.
Forecast all variables given the hypothesis by supplying the conditioning data CondF. Supply the estimation sample as a presample to initialize the model.
Y = forecast(EstMdl,numperiods,FRED.Variables,YF=CondF);
Y is a 12-by-7 matrix of forecasts and the fixed values in the column corresponding to FEDFUNDS.
Plot the forecasts with the last few periods of the estimation sample.
fh = dateshift(FRED.Time(end),"end","quarter",1:numperiods); idx = find(~idxFF); figure; ht = tiledlayout(2,2); for j = idx(1:4) nexttile h1 = plot(FRED.Time((end-49):end),FRED{(end-49):end,j}); hold on h2 = plot(fh,Y(:,j)); title(EstMdl.SeriesNames(j)); xlabel("Date"); h = gca; fill([FRED.Time(end) fh([end end]) FRED.Time(end)],h.YLim([1 1 2 2]),"k", ... FaceAlpha=0.1,EdgeColor="none"); legend([h1 h2],"True","Forecast",Location="best") hold off end title(ht,"Forecasts With FEDFUNDS = 0.5")
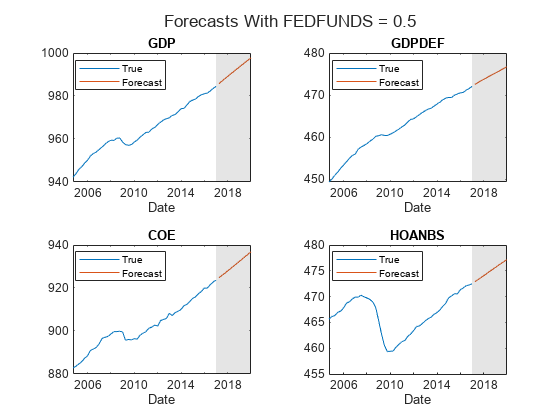
figure; ht = tiledlayout(2,1); for j = idx(5:6) nexttile h1 = plot(FRED.Time((end-49):end),FRED{(end-49):end,j}); hold on h2 = plot(fh,Y(:,j)); title(EstMdl.SeriesNames(j)); xlabel("Date"); h = gca; fill([FRED.Time(end) fh([end end]) FRED.Time(end)],h.YLim([1 1 2 2]),"k", ... FaceAlpha=0.1,EdgeColor="none"); legend([h1 h2],"True","Forecast",Location="best") hold off end title(ht,"Forecasts With FEDFUNDS = 0.5")

Analyze forecast accuracy using forecast intervals over a three-year horizon. This example follows from Return Matrix of VEC Model Forecasts.
Load the Data_USEconVECModel data set and preprocess the data.
load Data_USEconVECModel
FRED.GDP = 100*log(FRED.GDP);
FRED.GDPDEF = 100*log(FRED.GDPDEF);
FRED.COE = 100*log(FRED.COE);
FRED.HOANBS = 100*log(FRED.HOANBS);
FRED.PCEC = 100*log(FRED.PCEC);
FRED.GPDI = 100*log(FRED.GPDI);Estimate a VEC(1) model. Reserve the last three years of data to assess forecast accuracy. Assume that the appropriate cointegration rank is 4, and the H1 Johansen form is appropriate for the model.
bfh = FRED.Time(end) - years(3);
estIdx = FRED.Time < bfh;
Mdl = vecm(7,4,1);
Mdl.SeriesNames = FRED.Properties.VariableNames;
EstMdl = estimate(Mdl,FRED{estIdx,:});Forecast responses from the estimated model over a three-year horizon. Specify all in-sample observations as a presample. Return the MSE of the forecasts.
numperiods = 12;
Y0 = FRED{estIdx,:};
[Y,YMSE] = forecast(EstMdl,numperiods,Y0);Y is a 12-by-7 matrix of forecasted responses. YMSE is a 12-by-1 cell vector of 7-by-7 matrices corresponding to the MSEs.
Extract the main diagonal elements from the matrices in each cell of YMSE. Apply the square root of the result to obtain standard errors.
extractMSE = @(x)diag(x)'; MSE = cellfun(extractMSE,YMSE,UniformOutput=false); SE = sqrt(cell2mat(MSE));
Estimate approximate 95% forecast intervals for each response series.
YFI = zeros(numperiods,Mdl.NumSeries,2); YFI(:,:,1) = Y - 2*SE; YFI(:,:,2) = Y + 2*SE;
Plot the forecasted responses and the last 40 true responses.
figure ht = tiledlayout(2,2); for j = 1:4 nexttile h1 = plot(FRED.Time((end-39):end),FRED{(end-39):end,j}); hold on h2 = plot(FRED.Time(~estIdx),Y(:,j)); h3 = plot(FRED.Time(~estIdx),YFI(:,j,1),"k--"); plot(FRED.Time(~estIdx),YFI(:,j,2),"k--"); title(EstMdl.SeriesNames(j)); xlabel("Date"); h = gca; fill([bfh h.XLim([2 2]) bfh],h.YLim([1 1 2 2]),"k", ... FaceAlpha=0.1,EdgeColor="none"); legend([h1 h2 h3],"Observed","Forecast","Forecast interval", ... Location="best"); hold off end title(ht,"Forecasts and 95% Forecast Intervals")
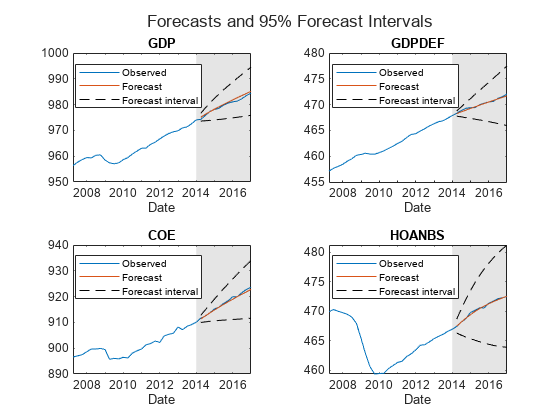
figure ht = tiledlayout(2,2); for j = 5:7 nexttile h1 = plot(FRED.Time((end-39):end),FRED{(end-39):end,j}); hold on h2 = plot(FRED.Time(~estIdx),Y(:,j)); h3 = plot(FRED.Time(~estIdx),YFI(:,j,1),"k--"); plot(FRED.Time(~estIdx),YFI(:,j,2),"k--"); title(EstMdl.SeriesNames(j)); xlabel("Date"); h = gca; fill([bfh h.XLim([2 2]) bfh],h.YLim([1 1 2 2]),"k", ... FaceAlpha=0.1,EdgeColor="none"); legend([h1 h2 h3],"Observed","Forecast","Forecast interval", ... Location="best"); hold off end title(ht,"Forecasts and 95% Forecast Intervals")
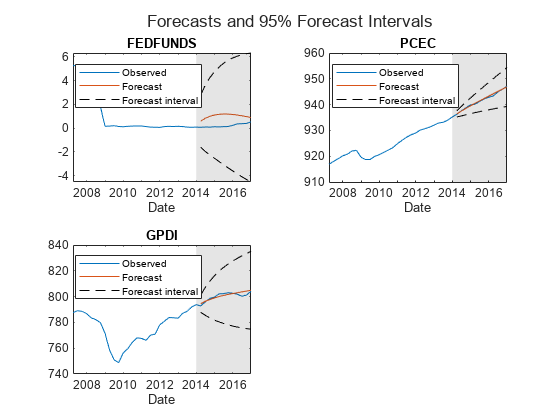
Since R2022b
Consider a VEC model for the following seven macroeconomic series, and then fit the model to a timetable of response data. This example is based on Return Matrix of VEC Model Forecasts.
Load and Preprocess Data
Load the Data_USEconVECModel data set.
load Data_USEconVECModel
DTT = FRED;
DTT.GDP = 100*log(DTT.GDP);
DTT.GDPDEF = 100*log(DTT.GDPDEF);
DTT.COE = 100*log(DTT.COE);
DTT.HOANBS = 100*log(DTT.HOANBS);
DTT.PCEC = 100*log(DTT.PCEC);
DTT.GPDI = 100*log(DTT.GPDI);Prepare Timetable for Estimation
When you plan to supply a timetable directly to estimate, you must ensure it has all the following characteristics:
All selected response variables are numeric and do not contain any missing values.
The timestamps in the
Timevariable are regular, and they are ascending or descending.
Remove all missing values from the table.
DTT = rmmissing(DTT); T = height(DTT)
T = 240
DTT does not contain any missing values.
Determine whether the sampling timestamps have a regular frequency and are sorted.
areTimestampsRegular = isregular(DTT,"quarters")areTimestampsRegular = logical
0
areTimestampsSorted = issorted(DTT.Time)
areTimestampsSorted = logical
1
areTimestampsRegular = 0 indicates that the timestamps of DTT are irregular. areTimestampsSorted = 1 indicates that the timestamps are sorted. Macroeconomic series in this example are timestamped at the end of the month. This quality induces an irregularly measured series.
Remedy the time irregularity by shifting all dates to the first day of the quarter.
dt = DTT.Time; dt = dateshift(dt,"start","quarter"); DTT.Time = dt;
DTT is regular with respect to time.
Create Model Template for Estimation
Create a VEC(1) model by using the shorthand syntax. Specify the variable names.
Mdl = vecm(7,4,1); Mdl.SeriesNames = DTT.Properties.VariableNames;
Mdl is a vecm model object. All properties containing NaN values correspond to parameters to be estimated given data.
Fit Model to Data
Estimate the model by supplying the timetable of data DTT. By default, because the number of variables in Mdl.SeriesNames is the number of variables in DTT, estimate fits the model to all the variables in DTT.
EstMdl = estimate(Mdl,DTT);
EstMdl is an estimated vecm model object.
Forecast Responses and Compute Forecast MSEs
Forecast responses from the estimated model over a three-year horizon. Specify the entire data set DTT as a presample observations.
numperiods = 12; [Tbl,YMSE] = forecast(EstMdl,numperiods,DTT); size(Tbl)
ans = 1×2
12 7
tail(DTT)
Time GDP GDPDEF COE HOANBS FEDFUNDS PCEC GPDI
___________ ______ ______ ______ ______ ________ ______ ______
01-Jan-2015 978.6 469.42 915.93 470.1 0.11 940.09 802.11
01-Apr-2015 979.8 469.97 917.34 470.57 0.13 941.25 802.29
01-Jul-2015 980.6 470.28 918.4 470.52 0.14 942.2 803.01
01-Oct-2015 981.04 470.51 919.95 471.33 0.24 942.86 802.61
01-Jan-2016 981.37 470.62 919.95 471.67 0.36 943.33 801.86
01-Apr-2016 982.28 471.19 921.5 472.09 0.38 944.88 800.22
01-Jul-2016 983.5 471.54 922.78 472.24 0.4 945.97 801.21
01-Oct-2016 984.48 472.06 923.69 472.47 0.54 947.12 804.13
head(Tbl)
Time GDP_Responses GDPDEF_Responses COE_Responses HOANBS_Responses FEDFUNDS_Responses PCEC_Responses GPDI_Responses
___________ _____________ ________________ _____________ ________________ __________________ ______________ ______________
01-Jan-2017 985.7 472.53 924.74 472.87 0.3725 948.18 806.74
01-Apr-2017 986.82 472.93 925.75 473.21 0.33795 949.24 808.66
01-Jul-2017 987.92 473.31 926.78 473.57 0.30002 950.29 810.45
01-Oct-2017 988.99 473.67 927.82 473.94 0.27518 951.35 812.12
01-Jan-2018 990.07 474.02 928.88 474.33 0.263 952.42 813.74
01-Apr-2018 991.14 474.37 929.95 474.74 0.26045 953.49 815.32
01-Jul-2018 992.22 474.71 931.04 475.15 0.26472 954.56 816.86
01-Oct-2018 993.29 475.05 932.14 475.56 0.27283 955.64 818.35
YMSE
YMSE=12×1 cell array
{7×7 double}
{7×7 double}
{7×7 double}
{7×7 double}
{7×7 double}
{7×7 double}
{7×7 double}
{7×7 double}
{7×7 double}
{7×7 double}
{7×7 double}
{7×7 double}
YMSE{6}ans = 7×7
7.6245 1.6879 7.7978 6.3846 3.5735 5.2342 26.8879
1.6879 1.9506 1.7640 0.4391 1.6560 1.2281 4.4627
7.7978 1.7640 8.8184 6.9137 3.6937 5.4552 28.3538
6.3846 0.4391 6.9137 7.4894 2.9271 4.2783 25.3822
3.5735 1.6560 3.6937 2.9271 4.3945 2.1872 12.6306
5.2342 1.2281 5.4552 4.2783 2.1872 4.1945 18.0819
26.8879 4.4627 28.3538 25.3822 12.6306 18.0819 113.1428
Tbl is a 12-by-7 matrix of forecasted responses (denoted responseVariable_Responses). The timestamps of Tbl follow directly from the timestamps of DTT, and they have the same sampling frequency. YMSE is a 12-by-1 cell array of 7-by-7 forecast MSE matrices. For example, the forecast covariance of GDP and COE in period 6 of the forecast horizon if element (1,3) of the matrix in YMSE{6}, which is 7.7978.
Since R2022b
Consider the model and data in Return Matrix of VEC Model Forecasts.
Load Data
Load the Data_USEconVECModel data set.
load Data_USEconVECModelThe Data_Recessions data set contains the beginning and ending serial dates of recessions. Load this data set. Convert the matrix of date serial numbers to a datetime array.
load Data_Recessions dtrec = datetime(Recessions,ConvertFrom="datenum");
Preprocess Data
Remove the exponential trend from the series, and then scale them by a factor of 100.
DTT = FRED; DTT.GDP = 100*log(DTT.GDP); DTT.GDPDEF = 100*log(DTT.GDPDEF); DTT.COE = 100*log(DTT.COE); DTT.HOANBS = 100*log(DTT.HOANBS); DTT.PCEC = 100*log(DTT.PCEC); DTT.GPDI = 100*log(DTT.GPDI);
Create a dummy variable that identifies periods in which the U.S. was in a recession or worse. Specifically, the variable should be 1 if FRED.Time occurs during a recession, and 0 otherwise. Include the variable with the FRED data.
isin = @(x)(any(dtrec(:,1) <= x & x <= dtrec(:,2))); DTT.IsRecession = double(arrayfun(isin,DTT.Time));
Prepare Timetable for Estimation
Remove all missing values from the table.
DTT = rmmissing(DTT);
To make the series regular, shift all dates to the first day of the quarter.
dt = DTT.Time; dt = dateshift(dt,"start","quarter"); DTT.Time = dt;
DTT is regular with respect to time.
Create Model Template for Estimation
Create a VEC(1) model using the shorthand syntax. Assume that the appropriate cointegration rank is 4. You do not have to specify the presence of a regression component when creating the model. Specify the variable names.
Mdl = vecm(7,4,1); Mdl.SeriesNames = DTT.Properties.VariableNames(1:end-1);
Fit Model to Data
Estimate the model using all but the last three years of data. Specify the predictor identifying whether the observation was measured during a recession.
bfh = DTT.Time(end) - years(3);
fh = DTT.Time(DTT.Time >= bfh);
EstSample = DTT(DTT.Time < bfh,:);
FSample = DTT(fh,:);
EstMdl = estimate(Mdl,EstSample,PredictorVariables="IsRecession");Forecast Responses
Forecast a path of quarterly responses three years into the future.
numperiods = numel(fh); Tbl = forecast(EstMdl,numperiods,EstSample, ... InSample=FSample,PredictorVariables="IsRecession"); head(Tbl(:,endsWith(Tbl.Properties.VariableNames,"_Responses")))
Time GDP_Responses GDPDEF_Responses COE_Responses HOANBS_Responses FEDFUNDS_Responses PCEC_Responses GPDI_Responses
___________ _____________ ________________ _____________ ________________ __________________ ______________ ______________
01-Jan-2014 974.87 468.25 911.21 467.31 0.47511 936.25 793.63
01-Apr-2014 975.81 468.6 912.19 467.82 0.63807 937.22 794.68
01-Jul-2014 976.67 468.91 913.19 468.3 0.72011 938.16 795.47
01-Oct-2014 977.53 469.21 914.16 468.77 0.76135 939.08 796.33
01-Jan-2015 978.38 469.49 915.12 469.2 0.7691 939.98 797.17
01-Apr-2015 979.22 469.77 916.06 469.62 0.75747 940.86 798
01-Jul-2015 980.05 470.04 916.99 470.02 0.73223 941.74 798.83
01-Oct-2015 980.89 470.31 917.91 470.41 0.69828 942.62 799.67
Tbl is a 12-by-15 matrix of variables in FSample and forecasted responses (variables named responseVariable_Responses, for each response responseVariable in the model).
Plot the forecasted responses and the last 50 true responses.
figure; tiledlayout(2,2) for j = EstMdl.SeriesNames(1:4) nexttile h1 = plot(DTT.Time((end-49):end),DTT{(end-49):end,j}); hold on h2 = plot(Tbl.Time,Tbl{:,j+"_Responses"}); title(j); xlabel("Date"); h = gca; fill([DTT.Time(end) bfh([end end]) DTT.Time(end)],h.YLim([1 1 2 2]),"k", ... FaceAlpha=0.1,EdgeColor="none"); legend([h1 h2],"True","Forecast",Location="best") hold off end
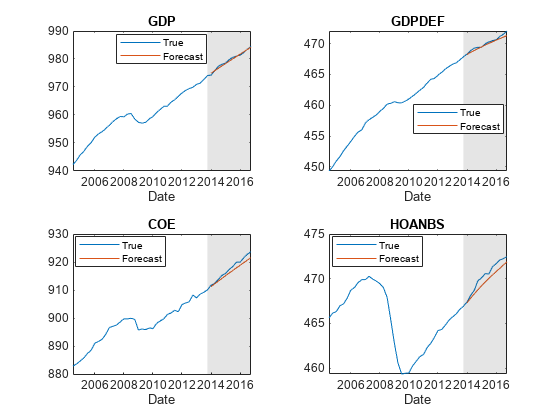
figure tiledlayout(2,2) for j = EstMdl.SeriesNames(5:7) nexttile h1 = plot(DTT.Time((end-49):end),DTT{(end-49):end,j}); hold on h2 = plot(Tbl.Time,Tbl{:,j+"_Responses"}); title(j); xlabel("Date"); h = gca; fill([DTT.Time(end) bfh([end end]) DTT.Time(end)],h.YLim([1 1 2 2]),"k", ... FaceAlpha=0.1,EdgeColor="none"); legend([h1 h2],"True","Forecast",Location="best") hold off end
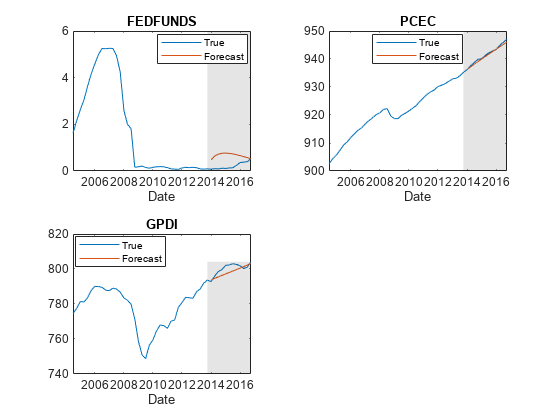
Since R2022b
This example is based on Return Timetable of Forecasts and Array of Forecast MSEs. Forecast all response variables of the VEC model into a 3-year forecast horizon beyond the sampling data, given that the effective federal funds rate FEDFUNDS is 0.5% during each future quarter.
Load and Preprocess Data
Load the Data_USEconVECModel data set.
load Data_USEconVECModel
DTT = FRED;
DTT.GDP = 100*log(DTT.GDP);
DTT.GDPDEF = 100*log(DTT.GDPDEF);
DTT.COE = 100*log(DTT.COE);
DTT.HOANBS = 100*log(DTT.HOANBS);
DTT.PCEC = 100*log(DTT.PCEC);
DTT.GPDI = 100*log(DTT.GPDI);Prepare Timetable for Estimation
Remove all missing values from the table.
DTT = rmmissing(DTT);
To make the series regular, shift all dates to the first day of the quarter.
dt = DTT.Time; dt = dateshift(dt,"start","quarter"); DTT.Time = dt;
DTT is regular with respect to time.
Create Model Template for Estimation
Create a VEC(1) model using the shorthand syntax. Specify the variable names.
Mdl = vecm(7,4,1); Mdl.SeriesNames = DTT.Properties.VariableNames;
Mdl is a vecm model object. All properties containing NaN values correspond to parameters to be estimated given data.
Fit Model to Data
Estimate the model. Pass the entire timetable DTT.
EstMdl = estimate(Mdl,DTT);
Prepare for Conditional Forecast of Estimated Model
Suppose economists hypothesize that the effective federal funds rate will be at 0.5% for the next 12 quarters.
Create a timetable with the following qualities:
The timestamps are regular with respect to the estimation sample timestamps and they are ordered from Q1 of 2017 through Q4 of 2019.
All variables of DTT, except for
FEDFUNDS, are a 12-by-1 vector ofNaNvalues.FEDFUNDSis a 12-by-1 vector, where each element is 0.5.
numperiods = 12;
shdt = DTT.Time(end) + calquarters(1:numperiods);
DTTCondF = retime(DTT,shdt,"fillwithmissing");
DTTCondF.FEDFUNDS = 0.5*ones(numperiods,1);DTTCondF is a 12-by-7 timetable that follows directly, in time, from DTT, and both timetables have the same variables. All variables in DTTCondF contain NaN values, except for FEDFUNDS, which is a vector composed of the value 0.5.
Perform Conditional Simulation of Estimated Model
Forecast all response variables, given the hypothesis, by supplying the conditioning data DTTCondF and specifying the response variable names. Supply the estimation sample as a presample to initialize the model.
Tbl = forecast(EstMdl,numperiods,DTT, ...
InSample=DTTCondF,ResponseVariables=EstMdl.SeriesNames);
size(Tbl)ans = 1×2
12 14
idx = endsWith(Tbl.Properties.VariableNames,"_Responses");
head(Tbl(:,idx)) Time GDP_Responses GDPDEF_Responses COE_Responses HOANBS_Responses FEDFUNDS_Responses PCEC_Responses GPDI_Responses
___________ _____________ ________________ _____________ ________________ __________________ ______________ ______________
01-Jan-2017 985.73 472.53 924.76 472.89 0.5 948.2 806.83
01-Apr-2017 986.89 472.96 925.8 473.27 0.5 949.27 808.96
01-Jul-2017 988.01 473.36 926.87 473.65 0.5 950.34 810.86
01-Oct-2017 989.12 473.74 927.94 474.04 0.5 951.42 812.62
01-Jan-2018 990.22 474.12 929.04 474.45 0.5 952.5 814.28
01-Apr-2018 991.31 474.49 930.14 474.85 0.5 953.59 815.85
01-Jul-2018 992.39 474.86 931.25 475.25 0.5 954.67 817.35
01-Oct-2018 993.47 475.24 932.36 475.65 0.5 955.76 818.79
Tbl is a 12-by-14 matrix of forecasts of all response variables of the VEC model in the forecast horizon, given FEDFUNDS is 0.5%. GDP_Responses contains the forecasts of the transformed GDP series. FEDFUNDS_Responses is a 12-by-1 vector composed of the value 0.5.
Since R2022b
This example is based on Return Timetable of Forecasts and Array of Forecast MSEs. Forecast all response variables of the VEC model into a 1-year forecast horizon beyond the sampling data, given several hypotheses economists make on the effective federal funds rate FEDFUNDS during each quarter of the next year after the sampling period.
Load the Data_USEconVECModel data set.
load Data_USEconVECModel
DTT = FRED;
DTT.GDP = 100*log(DTT.GDP);
DTT.GDPDEF = 100*log(DTT.GDPDEF);
DTT.COE = 100*log(DTT.COE);
DTT.HOANBS = 100*log(DTT.HOANBS);
DTT.PCEC = 100*log(DTT.PCEC);
DTT.GPDI = 100*log(DTT.GPDI);Remove all missing values from the table.
DTT = rmmissing(DTT);
To make the series regular, shift all dates to the first day of the quarter.
dt = DTT.Time; dt = dateshift(dt,"start","quarter"); DTT.Time = dt;
DTT is regular with respect to time.
Create a VEC(1) model using the shorthand syntax. Specify the variable names.
Mdl = vecm(7,4,1); Mdl.SeriesNames = DTT.Properties.VariableNames;
Estimate the model. Pass the entire timetable DTT.
EstMdl = estimate(Mdl,DTT);
Assuming the effective federal funds rate is 0.1%, 0.25%, 0.5%, 0.75%, and 1% percent throughout a 1-year forecast horizon, generate a forecast path for all response variables under each scenario.
Create a timetable with the following qualities:
The timestamps are regular with respect to the estimation sample timestamps and they are ordered from Q1 of 2017 through Q4 of 2017.
The variable
FEDFUNDSis a 4-by-5 matrix, where each column is composed of each of the assumptions on the value of the effective federal funds rate in the forecast horizon; the elements of the first column are 0.1, elements of the second column are 0.25, and so on.Each other response variable is a 4-by-5 matrix of
NaNvalues to be filled with forecasted paths byforecast.
numperiods = 4;
shdt = DTT.Time(end) + calquarters(1:numperiods);
DTTCondF = retime(DTT,shdt,"fillwithmissing");
DTTCondF = varfun(@(x)nan(numperiods,5),DTTCondF);
DTTCondF.Properties.VariableNames = EstMdl.SeriesNames;
DTTCondF.FEDFUNDS = ones(numperiods,1)*[0.1 0.25 0.5 0.75 1];
DTTCondFDTTCondF=4×7 timetable
Time GDP GDPDEF COE HOANBS FEDFUNDS PCEC GPDI
___________ _______________________________ _______________________________ _______________________________ _______________________________ ___________________________________ _______________________________ _______________________________
01-Jan-2017 NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN 0.1 0.25 0.5 0.75 1 NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN
01-Apr-2017 NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN 0.1 0.25 0.5 0.75 1 NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN
01-Jul-2017 NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN 0.1 0.25 0.5 0.75 1 NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN
01-Oct-2017 NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN 0.1 0.25 0.5 0.75 1 NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN
DTTCondF is a 4-by-7 timetable that follows directly, in time, from DTT, and both timetables have the same variables. Each variable in DTTCondF contains a 4-by-5 matrix of NaN values, except for FEDFUNDS, which is a matrix with each column containing a different scenario for the conditional forecasts.
Forecast all response variables, given the hypotheses, by supplying the conditioning data DTTCondF and specifying the response variable names. Supply the estimation sample as a presample to initialize the model. Return the forecast MSE matrices.
[Tbl,YMSE] = forecast(EstMdl,numperiods,DTT, ...
InSample=DTTCondF,ResponseVariables=EstMdl.SeriesNames);
size(Tbl)ans = 1×2
4 14
idx = endsWith(Tbl.Properties.VariableNames,"_Responses");
head(Tbl(:,idx)) Time GDP_Responses GDPDEF_Responses COE_Responses HOANBS_Responses FEDFUNDS_Responses PCEC_Responses GPDI_Responses
___________ ______________________________________________ ______________________________________________ ______________________________________________ ______________________________________________ ___________________________________ ______________________________________________ ______________________________________________
01-Jan-2017 985.65 985.68 985.73 985.77 985.82 472.51 472.52 472.53 472.54 472.55 924.7 924.72 924.76 924.79 924.82 472.83 472.85 472.89 472.94 472.98 0.1 0.25 0.5 0.75 1 948.14 948.16 948.2 948.23 948.27 806.54 806.65 806.83 807.01 807.2
01-Apr-2017 986.73 986.79 986.89 986.98 987.08 472.9 472.92 472.96 472.99 473.03 925.67 925.72 925.8 925.88 925.97 473.13 473.18 473.27 473.35 473.44 0.1 0.25 0.5 0.75 1 949.2 949.23 949.27 949.31 949.36 808.17 808.47 808.96 809.45 809.94
01-Jul-2017 987.83 987.9 988.01 988.12 988.24 473.26 473.29 473.36 473.42 473.48 926.69 926.76 926.87 926.97 927.08 473.5 473.55 473.65 473.74 473.84 0.1 0.25 0.5 0.75 1 950.26 950.29 950.34 950.4 950.45 810.06 810.36 810.86 811.36 811.86
01-Oct-2017 988.93 989 989.12 989.24 989.37 473.6 473.65 473.74 473.83 473.92 927.74 927.82 927.94 928.07 928.2 473.9 473.96 474.04 474.13 474.22 0.1 0.25 0.5 0.75 1 951.33 951.36 951.42 951.48 951.54 811.86 812.15 812.62 813.1 813.58
YMSE
YMSE=4×1 cell array
{7×7 double}
{7×7 double}
{7×7 double}
{7×7 double}
YMSE{4}ans = 7×7
2.9103 0.2459 2.6926 2.2954 0 1.9785 10.5522
0.2459 0.6435 0.2598 -0.2005 0 0.2656 0.1772
2.6926 0.2598 3.1251 2.3680 0 1.9150 10.3987
2.2954 -0.2005 2.3680 3.0306 0 1.5138 10.0253
0 0 0 0 0 0 0
1.9785 0.2656 1.9150 1.5138 0 1.7880 6.7155
10.5522 0.1772 10.3987 10.0253 0 6.7155 50.7359
Tbl is a 4-by-14 matrix of forecasts of all response variables of the VEC model in the forecast horizon, given each assumption on FEDFUNDS. GDP_Responses contains the matrix of 5 forecast paths of the transformed GDP series from matrix of 5 forecast paths. Each path uses the corresponding assumption about the value of FEDFUNDS_Responses.
YMSE is a 4-by-1 cell vector of 7-by-7 forecast MSE matrices for each period in the forecast horizon. The MSE matrices apply to each forecast path, and all elements of each matrix corresponding to the conditioning variable are 0.
Input Arguments
Forecast horizon, or the number of time points in the forecast period, specified as a positive integer.
Data Types: double
Presample response data that provides initial values for the forecasts, specified as a
numpreobs-by-numseries numeric matrix or a
numpreobs-by-numseries-by-numprepaths
numeric array. Use Y0 only when you supply optional data inputs as
numeric arrays.
numpreobs is the number of presample observations.
numseries is the number of response series
(Mdl.NumSeries). numprepaths is the number of
presample response paths.
Each row is a presample observation, and measurements in each row, among all pages,
occur simultaneously. The last row contains the latest presample observation.
Y0 must have at least Mdl.P rows. If you
supply more rows than necessary, forecast uses the latest
Mdl.P observations only.
Each column corresponds to the response series name in
Mdl.SeriesNames.
Pages correspond to separate, independent paths.
If you compute unconditional forecasts (that is, you do not specify the
YFname-value argument),forecastinitializes each forecasted path (page) using the corresponding page ofY0. Therefore, the output argumentYhasnumpaths=numprepathspages.If you compute conditional forecasts by specifying future response data in
YF:forecasttakes one of these actions:If
Y0is a matrix,forecastinitializes each response path (page) inYFusing the corresponding presample response inY0. Therefore,numpathsis the number of paths inYF, and all paths in the output argumentYderive from common initial conditions.If
YFis a matrix,forecastgeneratesnumprepathsforecast paths, initialized by each presample response path inY0, but the future response data, from which to condition the forecasts, is the same among all paths. Therefore,numprepathsis the number of paths in the output argumentY, and all paths evolve from possibly different initial conditions.Otherwise,
numpathsis the minimum betweennumprepathsand the number of pages inYF, andforecastappliesY0(:,:,to initialize forecasting pathj)jjnumpaths.
Data Types: double
Since R2022b
Presample response data that provides initial values for the forecasts, specified as a
table or timetable with numprevars variables and
numpreobs rows. forecast returns the
forecasted response variable in the output table or timetable Tbl2,
which is commensurate with Tbl1.
Each row is a presample observation, and measurements in each row, among all paths,
occur simultaneously. numpreobs must be at least
Mdl.P. If you supply more rows than necessary,
forecast uses the latest Mdl.P
observations only.
Each selected response variable is a
numpreobs-by-numprepaths numeric matrix. You
can optionally specify numseries response variables by using the
PresampleResponseVariables name-value argument.
Paths (columns) within a particular response variable are independent, but path
jjnumprepaths. The following conditions apply:
If you compute unconditional forecasts (that is, you do not specify the
InSampleandResponseVariablesname-value arguments),forecastinitializes each forecasted path per selected response variable using the corresponding path inTbl1. Therefore, each forecasted response variable in the output argumentTbl2is anumperiods-by-numprepathsmatrix.If you compute conditional forecasts by specifying future response data in
InSampleand corresponding response variables from the data by usingResponseVariables,forecasttakes one of these actions:If the selected presample response variables are vectors,
forecastinitializes each forecast path (column) of the selected response variables inInSampleby using the corresponding presample variable inTbl1. Therefore, all paths in the forecasted response variables evolve from common initial conditions.If the selected response variables in
InSampleare vectors,forecastgeneratesnumprepathsforecast paths, initialized by the paths of each selected presample response variable inTbl1, but the future response data, from which to condition the forecasts, is the same among all paths. Therefore,numpaths=numprepathsis the number of paths in all forecasted response variables, and all paths evolve from possibly different initial conditions.Otherwise,
numpathsis the minimum betweennumprepathsand the number of paths in each selected response variable inInSample. For each selected presample and future sample response variableResponseKjnumpaths,forecastappliesTbl1.to initialize the conditional forecast for the response data inResponseK(:,j)Tbl2.ResponseK(:,.j)
If Tbl1 is a timetable, all the following conditions must be true:
Tbl1must represent a sample with a regular datetime time step (seeisregular).The inputs
InSampleandTbl1must be consistent in time such thatTbl1immediately precedesInSamplewith respect to the sampling frequency and order.The datetime vector of sample timestamps
Tbl1.Timemust be ascending or descending.
If Tbl1 is a table, the last row contains the latest presample
observation.
Since R2022b
Future time series response or predictor data, specified as a table or timetable. InSample contains numvars variables, including numseries response variables yt or numpreds predictor variables xt for the model regression component. You can specify InSample only when you specify Tbl1.
Use InSample in the following situations:
Perform conditional simulation. You must also supply the response variable names to select response data in
InSampleby using theResponseVariablesname-value argument.Supply future predictor data for either unconditional or conditional simulation. To supply predictor data, you must specify predictor variable names in
InSampleby using thePredictorVariablesname-value argument. Otherwise,forecastignores the model regression component.
Each row corresponds to an observation in the forecast horizon, the first row is the earliest observation, and measurements in each row, among all paths, occur simultaneously. Specifically, row jVariableKInSample.) contains observations VariableK(j,:)jjInSample must have at least numperiods rows to cover the forecast horizon. If you supply more rows than necessary, forecast uses only the first numperiods rows.
Each selected response variable is a numeric matrix. For each selected response variable KjResponseKResponseKTbl1.) into the future. For each selected response variable ResponseKResponseK
If the selected presample response variables in
Tbl1are vectors,forecastinitializes each forecast path (column) of the selected response variables inInSampleby using the corresponding presample variable inTbl1. Therefore, all paths in the forecasted response variables of the outputTbl2evolve from common initial conditions.If the selected response variables in
InSampleare vectors,forecastgeneratesnumprepathsforecast paths, initialized by the paths of each selected presample response variable inTbl1, but the future response data, from which to condition the forecasts, is the same among all paths. Therefore,numpaths=numprepathsis the number of paths in all forecasted response variables, and all paths evolve from possibly different initial conditions.Otherwise,
numpathsis the minimum betweennumprepathsand the number of paths in each selected response variable inInSample. For each selected presample and future sample response variableResponseKjnumpaths,forecastappliesTbl1.to initialize the conditional forecast for the response data inResponseK(:,j)Tbl2.ResponseK(:,.j)
Each predictor variable is a numeric vector. All predictor variables are present in the regression component of each response equation and apply to all response paths.
If InSample is a timetable, the following conditions apply:
InSamplemust represent a sample with a regular datetime time step (seeisregular).The datetime vector
InSample.Timemust be ascending or descending.Tbl1must immediately precedeInSample, with respect to the sampling frequency.
If InSample is a table, the last row contains the latest
observation.
Elements of the response variables of InSample can be numeric scalars or missing values (indicated by NaN values). forecast treats numeric scalars as deterministic future responses that are known in advance, for example, set by policy. forecast forecasts responses for corresponding NaN values conditional on the known values. Elements of selected predictor variables must be numeric scalars.
By default, forecast computes conventional MMSE forecasts and forecast
MSEs without a regression component in the model (each selected response variable is a
numperiods-by-numprepaths matrix composed of
NaN values indicating a complete lack of knowledge of the future
state of the responses in the forecast horizon).
For more details, see Algorithms.
Example: Consider forecasting one path from a model composed of two
response series, GDP and CPI, three
periods into the future. Suppose that you have prior knowledge about some of
the future values of the responses, and you want to forecast the unknown
responses conditional on your knowledge. Specify InSample
as a matrix containing the values that you know, and use
NaN for values you do not know but want to forecast.
For example, InSample=array2table([2 NaN; 0.1 NaN; NaN
NaN],VariableNames=["GDP" "CPI"]) specifies that you have no
knowledge of the future values of CPI, but you know that
GDP is 2, 0.1, and unknown in periods 1, 2, and 3,
respectively, in the forecast horizon.
Since R2022b
Variables to select from InSample to treat as response variables
yt, specified as one of the following
data types:
String vector or cell vector of character vectors containing
numseriesvariable names inInSample.Properties.VariableNamesA length
numseriesvector of unique indices (integers) of variables to select fromInSample.Properties.VariableNamesA length
numvarslogical vector, whereResponseVariables(selects variablej) = truejInSample.Properties.VariableNames, andsum(ResponseVariables)isnumseries
The selected variables must be numeric vectors (single path) or matrices (columns represent multiple independent paths) of the same width.
To compute conditional forecasts, you must specify
ResponseVariables to select the response variables in
InSample for the conditioning data.
ResponseVariables applies only when you specify
InSample.
By default, forecast computes conventional MMSE forecasts and
forecast MSEs.
Example: ResponseVariables=["GDP" "CPI"]
Example: ResponseVariables=[true false true false] or
ResponseVariable=[1 3] selects the first and third table
variables as the response variables.
Data Types: double | logical | char | cell | string
Name-Value Arguments
Specify optional pairs of arguments as
Name1=Value1,...,NameN=ValueN, where Name is
the argument name and Value is the corresponding value.
Name-value arguments must appear after other arguments, but the order of the
pairs does not matter.
Before R2021a, use commas to separate each name and value, and enclose
Name in quotes.
Example: forecast(Mdl,10,Y0,X=Exo) returns a numeric array
containing a 10-period forecasted response path from Mdl and
the numeric matrix of presample response data Y0, and specifies
the numeric matrix of future predictor data for the model regression component in
the forecast horizon Exo.
Since R2022b
Variables to select from Tbl1 to use for presample data, specified
as one of the following data types:
String vector or cell vector of character vectors containing
numseriesvariable names inTbl1.Properties.VariableNamesA length
numseriesvector of unique indices (integers) of variables to select fromTbl1.Properties.VariableNamesA length
numprevarslogical vector, wherePresampleResponseVariables(selects variablej) = truejTbl1.Properties.VariableNames, andsum(PresampleResponseVariables)isnumseries
The selected variables must be numeric vectors and cannot contain missing values
(NaN).
PresampleResponseNames does not need to contain the same names as
in Mdl.SeriesNames; forecast uses the data
in selected variable
PresampleResponseVariables( as a
presample for j)Mdl.SeriesNames(.j)
If the number of variables in Tbl1 matches
Mdl.NumSeries, the default specifies all variables in
Tbl1. If the number of variables in Tbl1
exceeds Mdl.NumSeries, the default matches variables in
Tbl1 to names in Mdl.SeriesNames.
Example: PresampleResponseVariables=["GDP" "CPI"]
Example: PresampleResponseVariables=[true false true false] or
PresampleResponseVariable=[1 3] selects the first and third table
variables for presample data.
Data Types: double | logical | char | cell | string
Forecasted time series of predictor data xt
to include in the model regression component, specified as a numeric matrix containing
numpreds columns. Use X only when you supply
Y0.
numpreds is the number of predictor variables
(size(Mdl.Beta,2)).
Each row corresponds to an observation in the forecast horizon, and measurements in
each row occur simultaneously. Specifically, row
jX() contains the predictor
observations j,:)jjX must have at least numperiods rows. If you
supply more rows than necessary, forecast uses only the earliest
numperiods observations. The first row contains the earliest
observation. forecast does not use the regression component in
the presample period.
Each column is an individual predictor variable. All predictor variables are present in the regression component of each response equation.
forecast applies X to each path (page);
that is, X represents one path of observed predictors.
To maintain model consistency into the forecast horizon, specify forecasted predictors
when Mdl has a regression component.
By default, forecast excludes the regression component,
regardless of its presence in Mdl.
Data Types: double
Future multivariate response series data for conditional forecasting, specified as a numeric
matrix or array containing numseries columns. Use YF
only when you supply Y0.
Each row corresponds to observations in the forecast horizon, and the first row is the
earliest observation. Specifically, row j in sample path
k
(YF()
contains the responses j,:,k)j periods into the future, or the
jYF must have at least numperiods rows to cover
the forecast horizon. If you supply more rows than necessary,
forecast uses only the first numperiods
rows.
Each column corresponds to the response variable name in
Mdl.SeriesNames.
Each page corresponds to a separate sample path. Specifically, path
k (YF(:,:,)
captures the state, or knowledge, of the response series as they evolve from the presample
past (k)Y0) into the future.
If
YFis a matrix,forecastgeneratesnumprepathsforecast paths, initialized by each presample response path inY0, but the future response data, from which to condition the forecasts, is the same among all paths. Therefore,numprepathsis the number of paths in the output argumentY, and all paths evolve from possibly different initial conditions.If
Y0is a matrix,forecastinitializes each response path (page) inYFusing the corresponding presample response inY0. Therefore,numpathsis the number of paths inYF, and all paths in the output argumentYderive from common initial conditions.Otherwise,
numpathsis the minimum betweennumprepathsand the number of pages inYF, andforecastappliesY0(:,:,to initialize forecasting pathj)jjnumpaths.
Elements of YF can be numeric scalars or missing values (indicated by
NaN values). forecast treats numeric scalars
as deterministic future responses that are known in advance, for example, set by policy.
forecast forecasts responses for corresponding
NaN values conditional on the known values.
By default, YF is an array composed of NaN values
indicating a complete lack of knowledge of all responses in the forecast horizon. In this
case, forecast estimates conventional MMSE forecasts.
For more details, see Algorithms.
Example: Consider forecasting one path from a model composed of four
response series three periods into the future. Suppose that you have
prior knowledge about some of the future values of the responses, and
you want to forecast the unknown responses conditional on your
knowledge. Specify YF as a matrix containing the
values that you know, and use NaN for values you do
not know but want to forecast. For example, 'YF',[NaN 2 5 NaN;
NaN NaN 0.1 NaN; NaN NaN NaN NaN] specifies that you have
no knowledge of the future values of the first and fourth response
series; you know the value for period 1 in the second response series,
but no other value; and you know the values for periods 1 and 2 in the
third response series, but not the value for period 3.
Data Types: double
Since R2022b
Variables to select from InSample to treat as exogenous predictor
variables xt, specified as one of the following data types:
String vector or cell vector of character vectors containing
numpredsvariable names inInSample.Properties.VariableNamesA length
numpredsvector of unique indices (integers) of variables to select fromInSample.Properties.VariableNamesA length
numvarslogical vector, wherePredictorVariables(selects variablej) = truejInSample.Properties.VariableNames, andsum(PredictorVariables)isnumpreds
Regardless, selected predictor variable
jMdl.Beta(:,.j)
PredictorVariables applies only when you specify
InSample.
The selected variables must be numeric vectors and cannot contain missing values
(NaN).
By default, forecast excludes the regression component, regardless
of its presence in Mdl.
Example: PredictorVariables=["M1SL" "TB3MS" "UNRATE"]
Example: PredictorVariables=[true false true false] or
PredictorVariable=[1 3] selects the first and third table variables as
the response variables.
Data Types: double | logical | char | cell | string
Note
NaNvalues inY0andXindicate missing values.forecastremoves missing values from the data by list-wise deletion. IfY0is a 3-D array, thenforecastperforms these steps:Horizontally concatenate pages to form a
numpreobs-by-numpaths*numseriesmatrix.Remove any row that contains at least one
NaNfrom the concatenated data.
In the case of missing observations, the results obtained from multiple paths of
Y0can differ from the results obtained from each path individually.For missing values in
X,forecastremoves the corresponding row from each page ofYF. After row removal fromXandYF, if the number of rows is less thannumperiods,forecastissues an error.forecastissues an error when selected response variables fromTbl1and selected predictor variables fromInSamplecontain any missing values.
Output Arguments
MMSE forecasts of the multivariate response series, returned as a
numobs-by-numseries numeric matrix or a
numobs-by-numseries-by-numpaths
numeric array. forecast returns Y only when
you supply presample data Y0 as a numeric matrix or array.
Y represents the continuation of the presample responses in
Y0.
Each row is a time point in the simulation horizon. Specifically, row
j contains the j-period-ahead
forecasts. Values in a row, among all pages, occur simultaneously. The last row contains
the latest forecasted values.
Each column corresponds to the response series name in
Mdl.SeriesNames.
Pages correspond to separate, independently forecasted paths.
If you specify future responses for conditional forecasting using the YF
name-value argument, the known values in YF appear in the same
positions in Y. However, Y contains forecasted
values for the missing observations in YF.
Since R2022b
MMSE forecasts of multivariate response series and other variables, returned as a
table or timetable, the same data type as Tbl1.
forecast returns Tbl2 only when you
supply the inputs Tbl1.
Tbl2 contains the following variables:
The forecasted response paths within the
numperiodslength forecast horizon of the selected response series yt. Each forecasted response variable inTbl2is anumperiods-by-numpathsnumeric matrix, wherenumpathsdepends on the number of response paths in the specified presample or future sample data (seeTbl1orInSample). Each row corresponds to a time in the forecast horizon and each column corresponds to a separate path.forecastnames the forecasted response variableResponseKResponseK_ResponsesMdl.Series(isK)GDP,Tbl2contains a variable for the corresponding forecasted response with the nameGDP_Responses. If you specifyResponseVariables,ResponseKResponseVariable(. Otherwise,K)ResponseKPresampleResponseVariable(.K)If you specify
InSample, all specified future response variables.
If Tbl2 is a timetable, the following conditions hold:
The row order of
Tbl2, either ascending or descending, matches the row order ofInSample, when you specify it. If you do not specifyInSample, the row order ofTbl2is the same as the row orderTbl1.If you specify
InSample, row timesTbl2.TimeareInSample.Time(1:numperiods). Otherwise,Tbl2.Time(1)is the next time afterTbl1(end)relative to the sampling frequency, andTbl2.Time(2:numperiods)are the following times relative to the sampling frequency.
MSE matrices of the forecasted responses, returned as a numperiods-by-1
cell vector of numseries-by-numseries numeric
matrices. Cells of YMSE compose a time series of forecast error
covariance matrices. Cell j contains the
j-period-ahead MSE matrix.
YMSE is identical for all paths.
Because forecast treats predictor variables in X
as exogenous and nonstochastic, YMSE reflects the error covariance
associated with the autoregressive component of the input model Mdl
only.
Algorithms
forecastestimates unconditional forecasts using the equationwhere t = 1,...,
numperiods.forecastfilters anumperiods-by-numseriesmatrix of zero-valued innovations throughMdl.forecastuses specified presample innovations (Y0orTbl1) wherever necessary.forecastestimates conditional forecasts using the Kalman filter.forecastrepresents the VEC modelMdlas a state-space model (ssmmodel object) without observation error.forecastfilters the forecast dataYFthrough the state-space model. At period t in the forecast horizon, any unknown response iswhere s < t, is the filtered estimate of y from period s in the forecast horizon.
forecastuses specified presample values inY0orTbl1for periods before the forecast horizon.
The way
forecastdeterminesnumpaths, the number of paths (pages) in the output argumentY, or the number of paths (columns) in the forecasted response variables in the output argumentTbl2, depends on the forecast type.If you estimate unconditional forecasts, which means you do not specify the
YFname-value argument, orInSampleandResponseVariablesname-value arguments,numpathsis the number of paths in theY0orTbl1input argument.If you estimate conditional forecasts and the presample data
Y0and future sample dataYF, or response variables inTbl1andInSamplehave more than one path,numpathsis the fewest number of paths between the presample and future sample response data. Consequently,forecastuses only the firstnumpathspaths of each response variable for each input.If you estimate conditional forecasts and either
Y0orYF, or response variables inTbl1orInSamplehave one path,numpathsis the number of pages in the array with the most pages.forecastuses the variables with one path to produce each output path.
forecastsets the time origin of models that include linear time trends t0 tonumpreobs–Mdl.P(after removing missing values), wherenumpreobsis the number of presample observations. Therefore, the times in the trend component are t = t0 + 1, t0 + 2,..., t0 +numpreobs. This convention is consistent with the default behavior of model estimation in whichestimateremoves the firstMdl.Presponses, reducing the effective sample size. Althoughforecastexplicitly uses the firstMdl.Ppresample responses inY0orTbl1to initialize the model, the total number of usable observations determines t0. An observation inY0is usable if it does not contain aNaN.
References
[1] Hamilton, James D. Time Series Analysis. Princeton, NJ: Princeton University Press, 1994.
[2] Johansen, S. Likelihood-Based Inference in Cointegrated Vector Autoregressive Models. Oxford: Oxford University Press, 1995.
[3] Juselius, K. The Cointegrated VAR Model. Oxford: Oxford University Press, 2006.
[4] Lütkepohl, H. New Introduction to Multiple Time Series Analysis. Berlin: Springer, 2005.
Version History
Introduced in R2017bIn addition to accepting input data in numeric arrays,
forecast accepts input data in tables and timetables. forecast chooses default series on which to operate, but you can use the following name-value arguments to select variables.
PresampleResponseVariablesspecifies the response series names in the input presample response data.Insamplespecifies the table or regular timetable of future response and predictor data to compute conditional forecasts.ResponseVariablesspecifies the response series names inInSample.PredictorVariablesspecifies the predictor series inInSamplefor a model regression component.
MATLAB Command
You clicked a link that corresponds to this MATLAB command:
Run the command by entering it in the MATLAB Command Window. Web browsers do not support MATLAB commands.
Website auswählen
Wählen Sie eine Website aus, um übersetzte Inhalte (sofern verfügbar) sowie lokale Veranstaltungen und Angebote anzuzeigen. Auf der Grundlage Ihres Standorts empfehlen wir Ihnen die folgende Auswahl: .
Sie können auch eine Website aus der folgenden Liste auswählen:
So erhalten Sie die bestmögliche Leistung auf der Website
Wählen Sie für die bestmögliche Website-Leistung die Website für China (auf Chinesisch oder Englisch). Andere landesspezifische Websites von MathWorks sind für Besuche von Ihrem Standort aus nicht optimiert.
Amerika
- América Latina (Español)
- Canada (English)
- United States (English)
Europa
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)