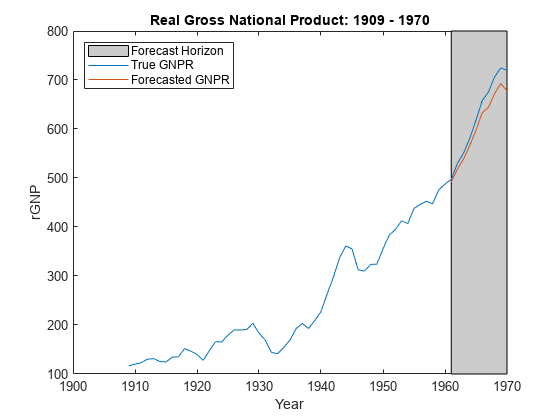
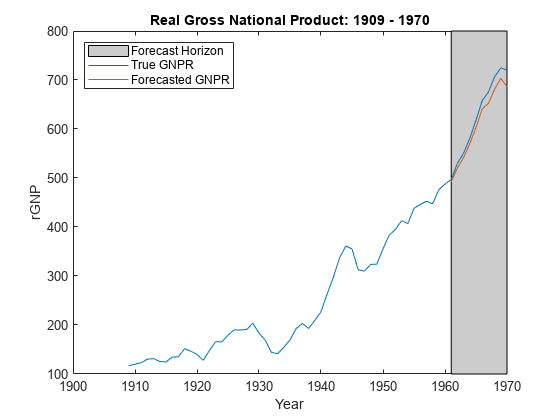
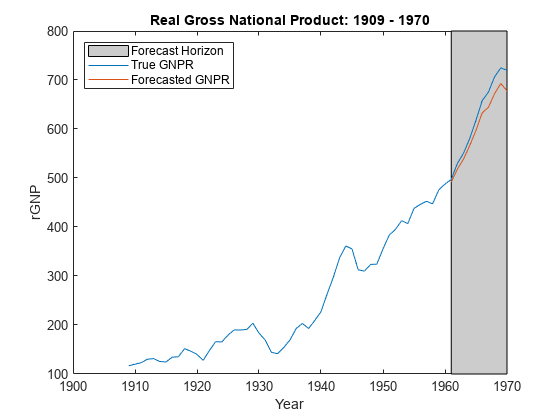
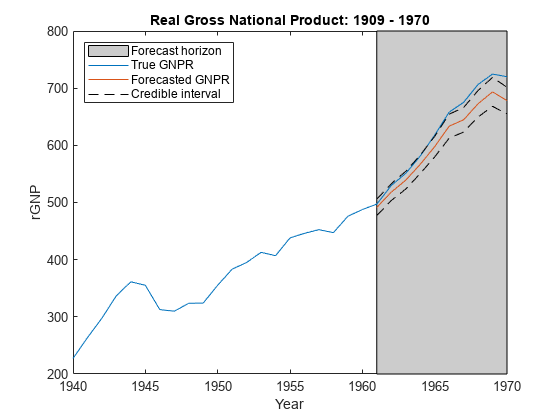
forecast
Forecast responses of Bayesian linear regression model
Syntax
Description
yF = forecast(Mdl,XF)numPeriods forecasted responses from the Bayesian linear regression
model
Mdl given the predictor data in XF, a
matrix with numPeriods rows.
To estimate the forecast, forecast uses the mean of
the numPeriods-dimensional posterior predictive distribution.
NaNs in the data indicate missing values, which
forecast removes using list-wise deletion.
yF = forecast(Mdl,XF,X,y)X and corresponding response
data y.
If
Mdlis a joint prior model, thenforecastproduces the posterior predictive distribution by updating the prior model with information about the parameters that it obtains from the data.If
Mdlis a posterior model, thenforecastupdates the posteriors with information about the parameters that it obtains from the additional data. The complete data likelihood is composed of the additional dataXandy, and the data that createdMdl.
yF = forecast(___,Name,Value)
Examples
Input Arguments
Name-Value Arguments
Output Arguments
Limitations
If Mdl is an empiricalblm model object, then you cannot specify
Beta or Sigma2. You cannot forecast from
conditional predictive distributions by using an empirical prior distribution.
More About
Tips
Monte Carlo simulation is subject to variation. If
forecastuses Monte Carlo simulation, then estimates and inferences might vary when you callforecastmultiple times under seemingly equivalent conditions. To reproduce estimation results, set a random number seed by usingrngbefore callingforecast.If
forecastissues an error while estimating the posterior distribution using a custom prior model, then try adjusting initial parameter values by usingBetaStartorSigma2Start, or try adjusting the declared log prior function, and then reconstructing the model. The error might indicate that the log of the prior distribution is–Infat the specified initial values.To forecasted responses from the conditional posterior predictive distribution of analytically intractable models, except empirical models, pass your prior model object and the estimation-sample data to
forecast. Then, specify theBetaname-value pair argument to forecast from the conditional posterior of σ2, or specify theSigma2name-value pair argument to forecast from the conditional posterior of β.
Algorithms
Whenever
forecastmust estimate a posterior distribution (for example, whenMdlrepresents a prior distribution and you supplyXandy) and the posterior is analytically tractable,forecastevaluates the closed-form solutions to Bayes estimators. Otherwise,forecastresorts to Monte Carlo simulation to forecast by using the posterior predictive distribution. For more details, see Posterior Estimation and Inference.This figure illustrates how
forecastreduces the Monte Carlo sample using the values ofNumDraws,Thin, andBurnIn. Rectangles represent successive draws from the distribution.forecastremoves the white rectangles from the Monte Carlo sample. The remainingNumDrawsblack rectangles compose the Monte Carlo sample.
Version History
Introduced in R2017a
See Also
Objects
conjugateblm|semiconjugateblm|diffuseblm|empiricalblm|customblm|mixconjugateblm|mixsemiconjugateblm|lassoblm