Lidar Localization with Unreal Engine Simulation
This example shows how to develop and evaluate a lidar localization algorithm using synthetic lidar data from the Unreal Engine® simulation environment.
One of the biggest challenges in developing a localization algorithm and evaluating its performance in varying conditions is obtaining ground truth. Although you can capture ground truth using expensive, high-precision inertial navigation systems (INS), virtual simulation is a cost-effective alternative. Simulation enables you to test under a variety of scenarios and sensor configurations. It also enables rapid development iteration and provides precise ground truth.
This example uses a prebuilt map of a parking lot scenario in the Unreal Engine simulation environment to develop and evaluate a lidar localization algorithm based on the normal distributions transform (NDT) approach. This example assumes a known initial pose of the vehicle.
Overview
Lidar localization is the process of estimating the lidar pose for a captured point cloud relative to a known point cloud map of the environment. Localization is a key technology for applications such as augmented reality, robotics, and automated driving. This example shows a lidar localization workflow with these steps:
Load a prebuilt map.
Localize on a given reference path using an NDT map.
Control the vehicle along a given reference path using the NDT localization estimate feedback.
Set Up Scenario in Simulation Environment
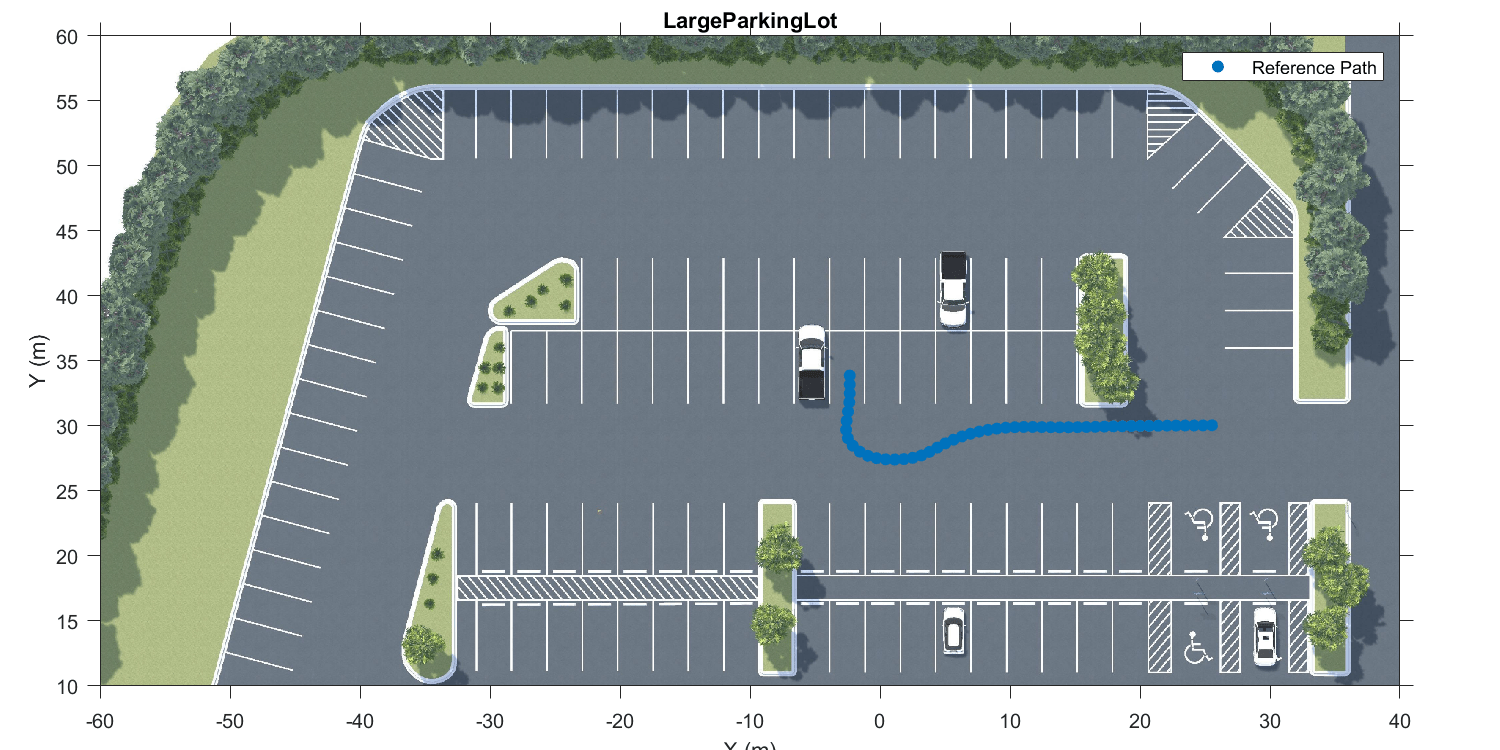
Parking a vehicle in a parking spot is a challenging maneuver that relies on accurate localization. Use the prebuilt Large Parking Lot scene to create this scenario. This example uses a recorded reference trajectory obtained by interactively selecting a sequence of waypoints from a scene. First, visualize the reference path using a 2-D bird's-eye view of the scene.
% Load reference path data = load("ReferencePathForward.mat"); refPosesX = data.ReferencePathForward.refPosesX; refPosesY = data.ReferencePathForward.refPosesY; refPosesT = data.ReferencePathForward.refPosesT; sceneName = "LargeParkingLot"; hScene = figure; helperShowSceneImage(sceneName); hold on scatter(refPosesX(:,2),refPosesY(:,2), [],"filled",DisplayName="Reference Path"); xlim([-60 40]) ylim([10 60]) hScene.Position = [100 100 1000 500]; % Resize figure legend hold off
Create NDT Map from Prebuilt Point Cloud Map
These are the steps to generate the prebuilt point cloud map:
Record the point clouds and the ground truth poses of the lidar sensor, while the ego vehicle moves along the known path in the environment. For more information about the path used to generate the map for this example, see Build Occupancy Map from 3-D Lidar Data Using SLAM.
Preprocess the point clouds to segment and remove the ground and the ego vehicle, and clip the point cloud to a select radius around the vehicle.
Align all the recorded point clouds using the known ground-truth poses with
pcalign.
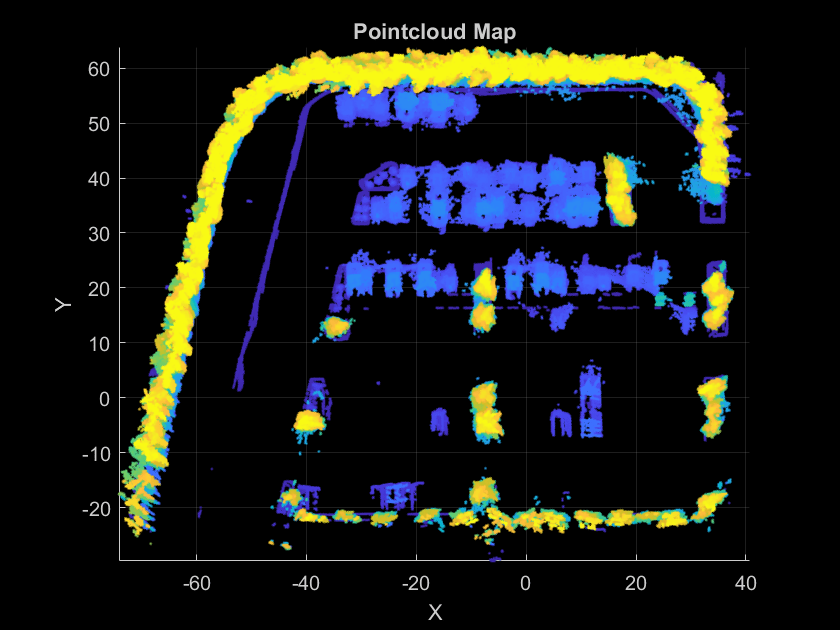
This example uses a map that has been prebuilt using these steps. Load and visualize the map.
load("parkingLotPCMapPoints.mat"); figure pcshow(ptCloudMapPoints) view(2) title("Pointcloud Map") xlabel("X") ylabel("Y")
Superimpose the point cloud map on the top-view image of the scene to visually examine how closely it resembles features in the scene.
hMapOnScene = helperSuperimposeMapOnSceneImage('LargeParkingLot', ptCloudMapPoints);
Create an NDT map from the above point cloud map using pcmapndt. Visualize the NDT map.
voxelSize = 1; ndtMap = pcmapndt(pointCloud(ptCloudMapPoints),voxelSize); figure show(ndtMap) view(2) title("NDT Map") xlabel("X") ylabel("Y")

Localize Using NDT Map
You can start the localization process with an initial estimate of the pose, which you can use to select a submap region around and begin pose estimation. This is more efficient than doing a global search in the entire map. In a real-world scenario, you can obtain an initial pose estimate at the entrance to the mapped environment using external sensors, such as a global navigation satellite system (GNSS) or fiducial markers, such as april tags or QR codes. As the vehicle moves into the mapped environment, the pose estimate obtained using localization from the previous time step is used as the initial pose estimate for the current time step.
These steps summarize the localization workflow presented in this example:
At the start of the simulation, use the initial pose estimate to select a submap of interest in the known NDT map, and obtain the actual pose estimate by localizing the point cloud in the NDT map.
Use the pose estimate obtained in the previous time step to check if the estimate is too close to the submap edge, or if it is outside the submap. If so, update the submap to a region around the pose estimate using
selectSubmap.Find the actual pose estimate by localizing the current point cloud in the NDT map using
findPose. Specify lower values for theTolerancename-value argument for accurate results.Repeat steps 2 and 3 for all subsequent timesteps along the reference trajectory.
The localizeUsingLidar model contains a hatchback vehicle moving along the specified reference path by using the Simulation 3D Vehicle with Ground Following block. A lidar sensor is mounted on the roof center of a vehicle using the Simulation 3D Lidar block. The Localize MATLAB Function Block and the helperLidarLocalizerNDT function implement the localization algorithm using the previously listed steps. Run the simulation to visualize the localization estimate and the ground truth pose of the vehicle along the reference trajectory.
close(hScene) if ismac error(['3D Simulation is supported only on Microsoft' char(174) ' Windows' char(174) ' and Linux' char(174) '.']); end % Open model modelName = "localizeUsingLidar"; open_system(modelName) snapnow % Run simulation simOut = sim(modelName);
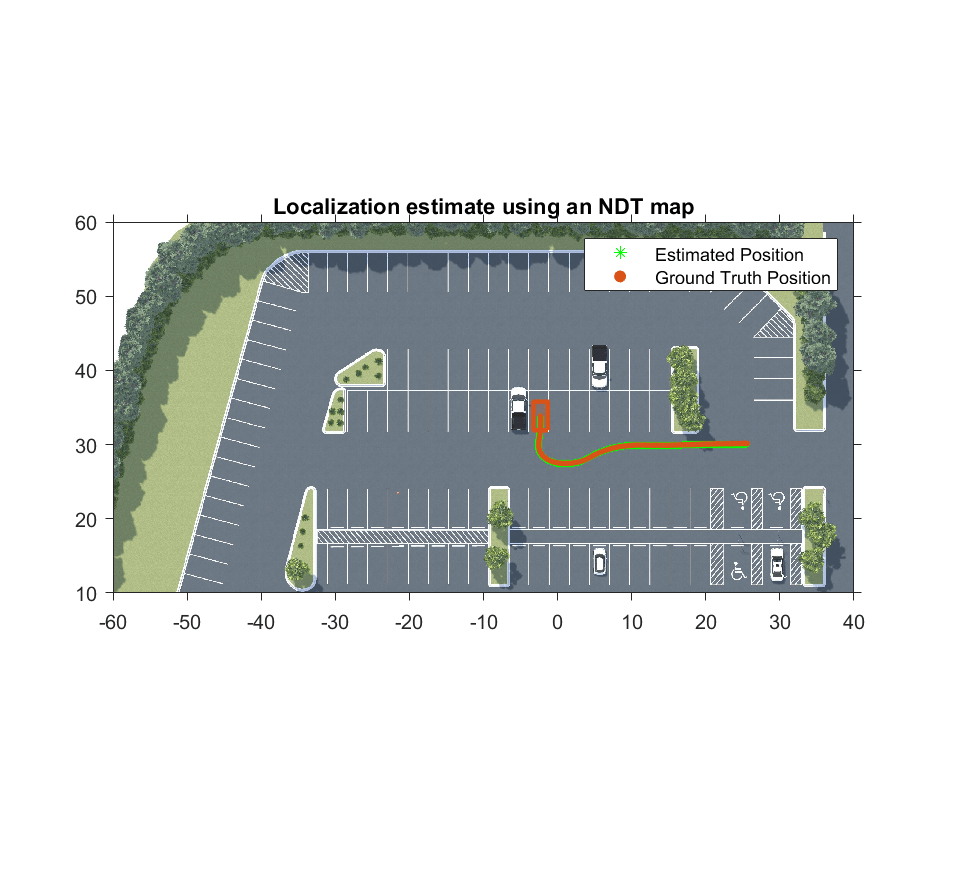
Evaluate Localization Accuracy
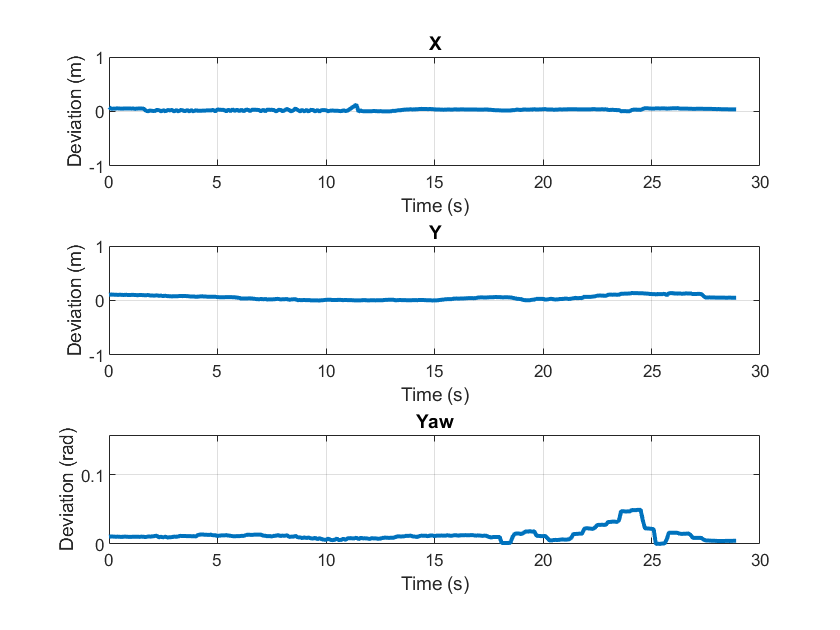
To quantify the efficacy of localization, measure the deviation in translation and rotation estimates compared to ground truth. Since the vehicle is moving on the flat ground, this example is concerned with motion in only the XY-plane.
hFigMetrics = helperDisplayMetrics(simOut);
Control Vehicle Using NDT Localization Estimate Feedback
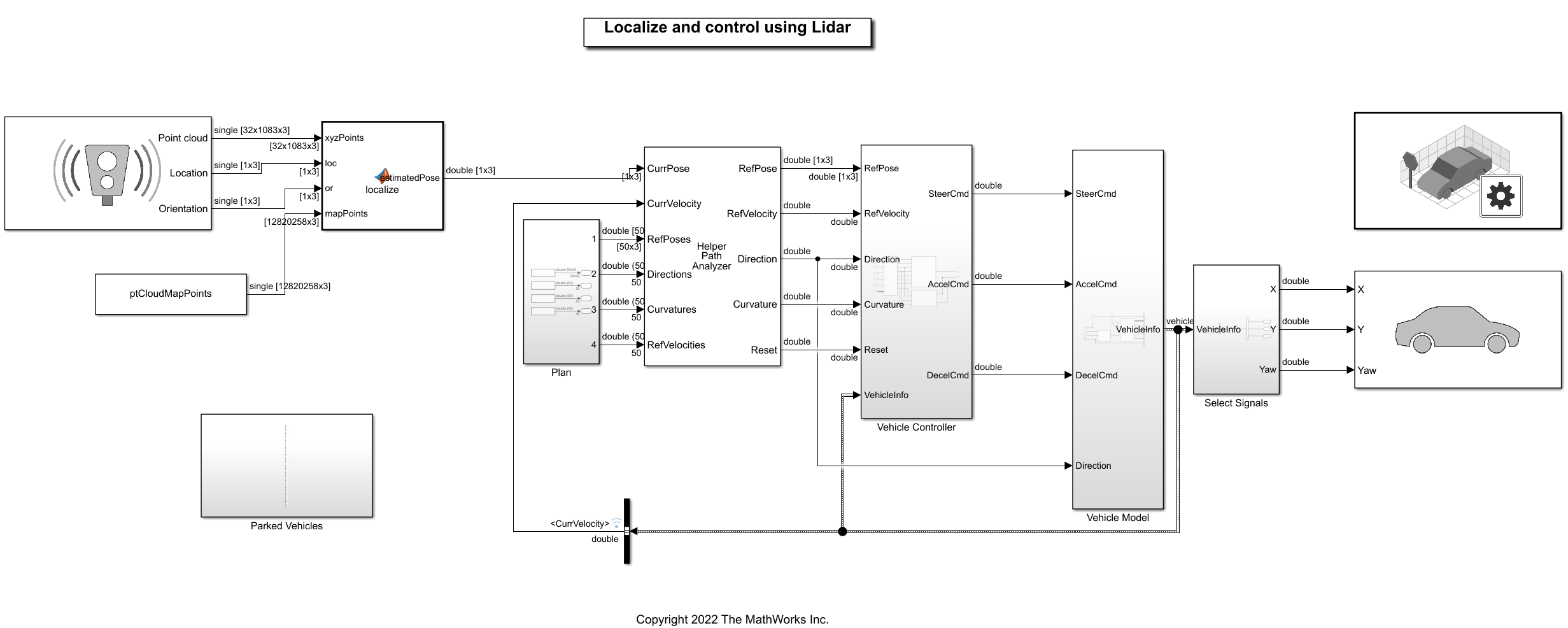
Metrics such as deviation in translation and rotation estimates are not, alone, enough to ensure the performance and accuracy of a localization system. For example, changes to the accuracy or performance of a localization system can affect the vehicle controller, requiring you to retune controller gains. Therefore, you must have a closed-loop verification framework that incorporates downstream components. The localizeAndControlUsingLidar model demonstrates this framework by incorporating a localization algorithm, vehicle controller, and suitable vehicle model.
The model has these main components:
The
Localizeblock is a MATLAB Function block that encapsulates the NDT map based localization algorithm implemented using thehelperLidarLocalizerNDTfunction. This block takes the lidar point cloud generated by the Simulation 3D Lidar block and the initial known pose as inputs and produces a localization estimate. The estimate is returned as , which represents the 2-D pose of the lidar in the map reference frame.The
Plansubsystem loads a preplanned trajectory from the workspace using therefPoses,directions,curvatures,andvelocitiesworkspace variables. The Path Smoother Spline block is used to compute therefPoses,directions,andcurvaturesvariables. The Velocity Profiler block computes thevelocitiesvariable.The Helper Path Analyzer block uses the reference trajectory and the current pose to feed the appropriate reference signal to the vehicle controller.
The
Vehicle Controllersubsystem controls the steering and velocity of the vehicle by using a lateral and longitudinal controller to produce steering and acceleration or deceleration commands, implemented by the Lateral Controller Stanley and Longitudinal Controller Stanley blocks. The subsystem feeds these commands to a vehicle model to simulate the dynamics of the vehicle in the simulation environment using the Vehicle Body 3DOF block.
% Specify vehicle dimensions centerToFront = 1.104; centerToRear = 1.343; frontOverhang = 0.828; rearOverhang = 0.589; vehicleWidth = 1.653; vehicleHeight = 1.513; vehicleLength = centerToFront + centerToRear + frontOverhang + rearOverhang; hatchbackDims = vehicleDimensions(vehicleLength,vehicleWidth,vehicleHeight, ... FrontOverhang=frontOverhang,RearOverhang=rearOverhang); vehicleDims = [hatchbackDims.Length hatchbackDims.Width hatchbackDims.Height]; vehicleColor = [0.85 0.325 0.098]; % Load workspace variables for preplanned trajectory refPoses = data.ReferencePathForward.Trajectory.refPoses; directions = data.ReferencePathForward.Trajectory.directions; curvatures = data.ReferencePathForward.Trajectory.curvatures; velocities = data.ReferencePathForward.Trajectory.velocities; startPose = refPoses(1,:); % Open model modelName = "localizeAndControlUsingLidar"; open_system(modelName) snapnow % Run simulation sim(modelName); close_system(modelName)
Supporting Functions
helperDisplayMetrics disaplays metrics to assess the quality of localization.
function hFig = helperDisplayMetrics(simOut) simTimes = simOut.logsout{1}.Values.Time; xEst = simOut.logsout{1}.Values.Data; yEst = simOut.logsout{2}.Values.Data; yawEst = simOut.logsout{3}.Values.Data; xTruth = squeeze(simOut.logsout{4}.Values.Data(:,1,:)); yTruth = squeeze(simOut.logsout{4}.Values.Data(:,2,:)); yawTruth = squeeze(simOut.logsout{5}.Values.Data(:,3,:)); xDeviation = abs(xEst - xTruth); yDeviation = abs(yEst - yTruth); yawDeviation = abs(helperWrapToPi(yawTruth - yawEst)); lim = [-1 1]; hFig = figure(Name="Metrics - Absolute Deviation"); subplot(3,1,1) plot(simTimes, xDeviation,LineWidth=2); ylim(lim) grid on title("X") xlabel("Time (s)") ylabel("Deviation (m)") subplot(3,1,2) plot(simTimes, yDeviation,LineWidth=2); ylim(lim) grid on title("Y") xlabel("Time (s)") ylabel("Deviation (m)") subplot(3,1,3) plot(simTimes, yawDeviation,LineWidth=2); ylim([0 pi/20]) grid on title("Yaw") xlabel("Time (s)") ylabel("Deviation (rad)") end
helperSuperImposeMapOnSceneImage superimposes point cloud map on scene image.
function hFig = helperSuperimposeMapOnSceneImage(sceneName, ptCloudAccum) hFig = figure(Name="Point Cloud Map"); hIm = helperShowSceneImage(sceneName); hold(hIm.Parent,"on") pcshow(ptCloudAccum); hold(hIm.Parent,"off") xlim(hIm.Parent, [-10 35]); ylim(hIm.Parent, [-23 20]); end
helperWrapToPi wraps angles to the range .
function angle = helperWrapToPi(angle) idx = (angle < -pi) | (angle > pi); angle(idx) = helperWrapTo2Pi(angle(idx) + pi) - pi; end
helperWrapTo2Pi wraps angles to the range .
function angle = helperWrapTo2Pi(angle) pos = (angle>0); angle = mod(angle, 2*pi); angle(angle==0 & pos) = 2*pi; end
See Also
Functions
pccat|pctransform|pcalign|pcviewset|pcplayer
Blocks
- Simulation 3D Scene Configuration | Simulation 3D Vehicle with Ground Following | Simulation 3D Lidar