Multistep Neural Network Prediction
Set Up in Open-Loop Mode
Dynamic networks with feedback, such as narxnet and narnet neural networks, can be transformed between
open-loop and closed-loop modes with the functions openloop and closeloop. Closed-loop networks make multistep
predictions. In other words they continue to predict when external feedback is missing, by using
internal feedback.
Here a neural network is trained to model the magnetic levitation system and simulated in the default open-loop mode.
[X,T] = maglev_dataset;
net = narxnet(1:2,1:2,10);
[x,xi,ai,t] = preparets(net,X,{},T);
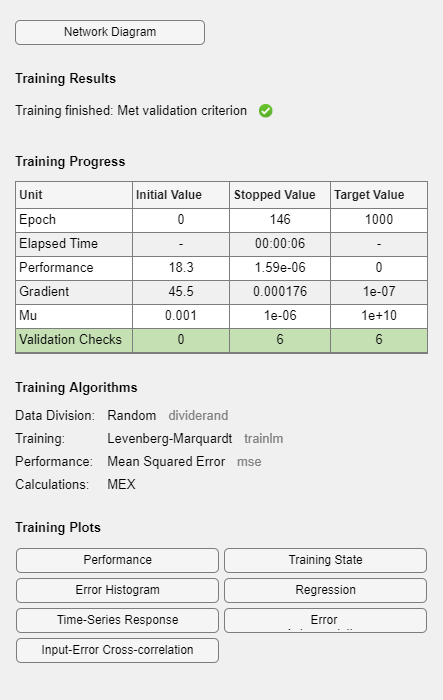
net = train(net,x,t,xi,ai);
y = net(x,xi,ai);
view(net)
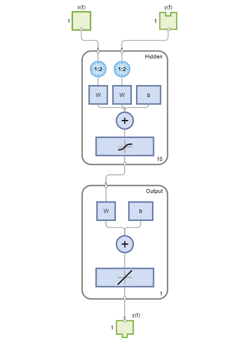
Multistep Closed-Loop Prediction From Initial Conditions
A neural network can also be simulated only in closed-loop form, so that given an external input series and initial conditions, the neural network performs as many predictions as the input series has time steps.
netc = closeloop(net); view(netc)
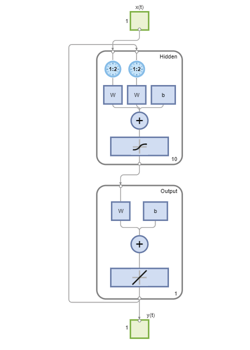
Here the training data is used to define the inputs x, and the initial
input and layer delay states, xi and ai, but they can be
defined to make multiple predictions for any input series and initial states.
[x,xi,ai,t] = preparets(netc,X,{},T);
yc = netc(x,xi,ai);Multistep Closed-Loop Prediction Following Known Sequence
It can also be useful to simulate a trained neural network up the present with all the known values of a time-series in open-loop mode, then switch to closed-loop mode to continue the simulation for as many predictions into the future as are desired.
Just as openloop and closeloop can be used to transform between open- and closed-loop neural networks,
they can convert the state of open- and closed-loop networks. Here are the full interfaces for
these functions.
[open_net,open_xi,open_ai] = openloop(closed_net,closed_xi,closed_ai); [closed_net,closed_xi,closed_ai] = closeloop(open_net,open_xi,open_ai);
Consider the case where you might have a record of the Maglev’s behavior for 20 time steps, and you want to predict ahead for 20 more time steps.
First, define the first 20 steps of inputs and targets, representing the 20 time steps
where the known output is defined by the targets t. With the next 20 time
steps of the input are defined, use the network to predict the 20 outputs using each of its
predictions feedback to help the network perform the next prediction.
x1 = x(1:20); t1 = t(1:20); x2 = x(21:40);
The open-loop neural network is then simulated on this data.
[x,xi,ai,t] = preparets(net,x1,{},t1);
[y1,xf,af] = net(x,xi,ai);Now the final input and layer states returned by the network are converted to closed-loop
form along with the network. The final input states xf and layer states
af of the open-loop network become the initial input states
xi and layer states ai of the closed-loop network.
[netc,xi,ai] = closeloop(net,xf,af);
Typically use preparets to define initial input and layer states.
Since these have already been obtained from the end of the open-loop simulation, you do not need
preparets to continue with the 20 step predictions of the closed-loop
network.
[y2,xf,af] = netc(x2,xi,ai);
Note that you can set x2 to different sequences of inputs to test
different scenarios for however many time steps you would like to make predictions. For example,
to predict the magnetic levitation system’s behavior if 10 random inputs are used:
x2 = num2cell(rand(1,10)); [y2,xf,af] = netc(x2,xi,ai);
Following Closed-Loop Simulation with Open-Loop Simulation
If after simulating the network in closed-loop form, you can continue the simulation from there in open-loop form. Here the closed-loop state is converted back to open-loop state. (You do not have to convert the network back to open-loop form as you already have the original open-loop network.)
[~,xi,ai] = openloop(netc,xf,af);
Now you can define continuations of the external input and open-loop feedback, and simulate the open-loop network.
x3 = num2cell(rand(2,10)); y3 = net(x3,xi,ai);
In this way, you can switch simulation between open-loop and closed-loop manners. One application for this is making time-series predictions of a sensor, where the last sensor value is usually known, allowing open-loop prediction of the next step. But on some occasions the sensor reading is not available, or known to be erroneous, requiring a closed-loop prediction step. The predictions can alternate between open-loop and closed-loop form, depending on the availability of the last step’s sensor reading.