Fit Custom Linear Models
About Custom Linear Models
In the Curve Fitter app, you can use the Custom Equation fit to define your own linear or nonlinear equations. The custom equation fit uses the nonlinear least-squares fitting procedure.
You can define a custom linear equation in Custom Equation, but the nonlinear fitting is less efficient and usually slower than linear least-squares fitting. If you need linear least-squares fitting for custom equations, select Linear Fitting instead. Linear models are linear combinations of (perhaps nonlinear) terms. They are defined by equations that are linear in the parameters.
Tip
If you need linear least-squares fitting for custom equations, choose Linear Fitting. If you don’t know if your equation can be expressed as a set of linear functions, then choose Custom Equation instead. See Selecting a Custom Equation Fit Interactively.
Selecting a Linear Fitting Custom Fit Interactively
In the Curve Fitter app, select some curve data. On the Curve Fitter tab, in the Data section, click Select Data. In the Select Fitting Data dialog box, select X data and Y data values.
Curve Fitter creates a default polynomial fit.
Change the model type. On the Curve Fitter tab, in the Fit Type section, click the arrow to open the gallery. In the gallery, click Linear Fitting in the Custom group.
In the Fit Options pane, an example equation appears when you click Linear Fitting.

You can change
xandyto any valid variable names.The lower box displays the example equation. Change the Coefficients and Terms entries to change the example terms and define your own equation.
For an example, see Fit Custom Linear Legendre Polynomials in Curve Fitter App.
Selecting Linear Fitting at the Command Line
To use a linear fitting algorithm, specify a cell array or string array of model terms as an
input to the fit or fittype functions. Do
not include coefficients in the expressions for the terms. If there is a constant
term, use '1' as the corresponding expression in the array.
To specify a linear model of the following form:
coeff1 * term1 + coeff2 * term2 + coeff3 * term3 + ...
term1,
term2, etc., use a cell array or string array where each
term, without coefficients, is specified as a separate element. For
example:LinearModelTerms = {'term1', 'term2', 'term3', ... }
Identify the linear model terms you need to input to
fittype. For example, the modelis linear ina*log(x) + b*x + c
a,b, andc. It has three termslog(x),x, and1(becausec=c*1). To specify this model you use these terms:LinearModelTerms = {'log(x)','x','1'}.Use the cell array or string array of linear model terms as the input to the
fittypefunction:linearfittype = fittype({'log(x)','x','1'})linearfittype = Linear model: linearfittype(a,b,c,x) = a*log(x) + b*x + cLoad some data and use the
fittypeas an input to thefitfunction.load census f = fit(cdate,pop,linearfittype)Alternatively, you can specify the cell array or string array of linear model terms as an input to thef = Linear model: f(x) = a*log(x) + b*x + c Coefficients (with 95% confidence bounds): a = -4.663e+04 (-4.973e+04, -4.352e+04) b = 25.9 (24.26, 27.55) c = 3.029e+05 (2.826e+05, 3.232e+05)fitfunction:f = fit(x,z,{'log(x)','x','1'})Plot the fit and data.
plot(f,cdate,pop)
For an example, see Fit Custom Linear Legendre Polynomials at the Command Line.
Fit Custom Linear Legendre Polynomials
Fit Custom Linear Legendre Polynomials in Curve Fitter App
This example shows how to fit data using several custom linear equations. The data is generated, and is based on the nuclear reaction 12C(e,e'α)8Be. The equations use sums of Legendre polynomial terms.
Consider an experiment in which 124 MeV electrons are scattered from 12C nuclei. In the subsequent reaction, alpha particles are emitted and produce the residual nuclei 8Be. By analyzing the number of alpha particles emitted as a function of angle, you can deduce certain information regarding the nuclear dynamics of 12C. The reaction kinematics are shown next.

The data is collected by placing solid state detectors at values of Θα ranging from 10o to 240o in 10o increments.
It is sometimes useful to describe a variable expressed as a function of angle in terms of Legendre polynomials
where Pn(x) is a
Legendre polynomial of degree n, x is
cos(Θα), and
an are the coefficients of the
fit. For information about generating Legendre polynomials, see the legendre function.
For the alpha-emission data, you can directly associate the coefficients with the nuclear dynamics by invoking a theoretical model. Additionally, the theoretical model introduces constraints for the infinite sum shown above. In particular, by considering the angular momentum of the reaction, a fourth-degree Legendre polynomial using only even terms should describe the data effectively.
You can generate Legendre polynomials with Rodrigues' formula:
Legendre Polynomials Up to Fourth Degree
n | Pn(x) |
|---|---|
0 | 1 |
1 | x |
2 | (1/2)(3x2– 1) |
3 | (1/2)(5x3 – 3x) |
4 | (1/8)(35x4 – 30x2 + 3) |
This example shows how to fit the data using a fourth-degree Legendre polynomial with only even terms:
Load the 12C alpha-emission data.
load carbon12alphaThe workspace now contains two new variables:
angleis a vector of angles (in radians) ranging from 10o to 240o in 10o increments.countsis a vector of raw alpha particle counts that correspond to the emission angles inangle.
Open the Curve Fitter app.
curveFitter
In the Curve Fitter app, on the Curve Fitter tab, in the Data section, click Select Data. In the Select Fitting Data dialog box, select
angleandcountsas the X data and Y data values, respectively, to create a default polynomial fit to the two variables.Change the fit type to a default custom linear fit. On the Curve Fitter tab, in the Fit Type section, click the arrow to open the gallery. In the gallery, click Linear Fitting in the Custom group.

Use Linear Fitting instead of the Custom Equation fit type because the Legendre polynomials depend only on the predictor variable and constants. The equation you will specify for the model is y1(x) (that is, the equation given at the beginning of this procedure). Because
angleis given in radians, the argument of the Legendre terms is given by cos(Θα).In the Fit Options pane, change the equation terms.
Change the Coefficients names to
a2,a4, anda0.Change the Terms value for
a2to the following:(1/2)*(3*cos(x)^2-1)
The Curve Fitter app updates the fit as you edit the terms.
Change the Terms value for
a4to the following:(1/8)*(35*cos(x)^4-30*cos(x)^2+3)

The fit appears in the Curve Fitter app.
In the Table Of Fits pane, double-click the Fit name value and change it to
Leg4Even.
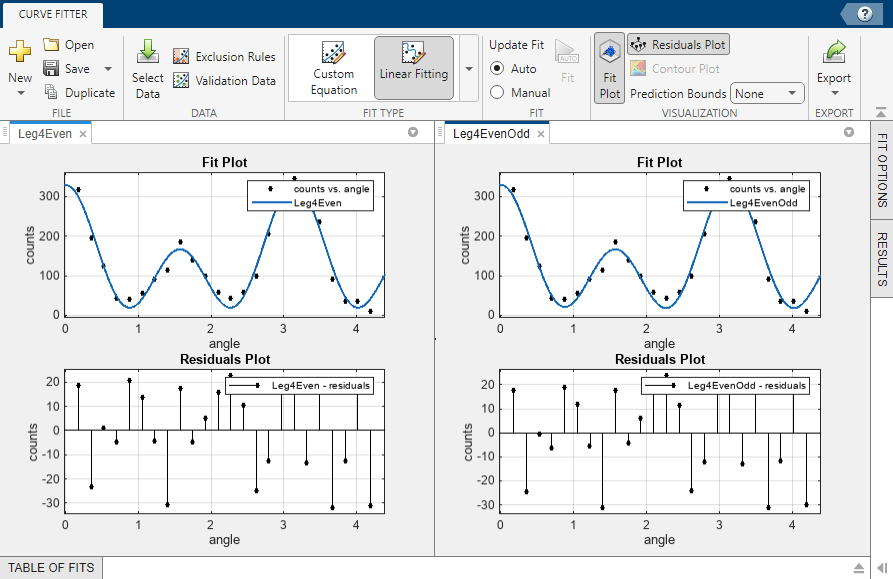
Display the residuals. On the Curve Fitter tab, in the Visualization section, click Residuals Plot.

The fit appears to follow the trend of the data well, while the residuals appear to be randomly distributed and do not exhibit any systematic behavior.
Examine the numerical fit results in the Results pane. Look at each coefficient value and its confidence bounds in parentheses. The 95% confidence bounds indicate that the coefficients associated with a0(x) and a4(x) are known fairly accurately, but that the a2(x) coefficient has a relatively large uncertainty.

To confirm the theoretical argument that the alpha-emission data is best described by a fourth-degree Legendre polynomial with only even terms, next fit the data using both even and odd terms:
First, make a copy of the Legendre polynomial fit to modify. On the Curve Fitter tab, in the File section, click Duplicate. The duplicated fit appears in a new tab in the Fits pane.
In the Table Of Fits pane, rename the new fit to
Leg4EvenOdd.In the Fit Options pane, change the equation terms.
Edit the terms as follows to fit the model given by y2(x):
Click the last + button twice, to add the odd Legendre terms.
Change the new coefficient names to
a1anda3.Change the Terms value for
a1to the following:cos(x)
Change the Terms value for
a3to the following:(1/2)*(5*cos(x)^3-3*cos(x))

Observe the new fit plotted in the Curve Fitter app, and examine the numerical results in the Results pane.

Note that the odd Legendre coefficients (
a1anda3) are likely candidates for removal to simplify the fit because their values are small and their confidence bounds contain zero. These results indicate that the odd Legendre terms do not contribute significantly to the fit, and the even Legendre terms are essentially unchanged from the previous fit. This confirms that the initial model choice in theLeg4Evenfit is the best one.Compare the fits side by side. Click the Document Actions button located to the far right of the fit figure tabs. Select the
Tile Alloption and specify a 1-by-2 layout.
You can display only the plots by dragging and hiding the Fit Options, Results, and Table Of Fits panes.
Fit Custom Linear Legendre Polynomials at the Command Line
Fit the same model at the command line that you created in the Curve Fitter app.
To use a linear fitting algorithm, specify a cell array or string array of model terms as an input to the
fittypefunction. Use the same Terms you entered in the Curve Fitter app for theLeg4Evenfit, and do not specify any coefficients.linearft = fittype({'(1/2)*(3*cos(x)^2-1)', ... '(1/8)*(35*cos(x)^4-30*cos(x)^2+3)','1'})linearft = Linear model: linearft(a,b,c,x) = a*((1/2)*(3*cos(x)^2-1))... + b*((1/8)*(35*cos(x)^4-30*cos(x)^2+3)) + cLoad the
angleandcountsvariables in the workspace.load carbon12alphaUse the
fittypeas an input to thefitfunction, and specify theangleandcountsvariables in the workspace.f = fit(angle,counts,linearft)
f = Linear model: f(x) = a*((1/2)*(3*cos(x)^2-1))... + b*((1/8)*(35*cos(x)^4-30*cos(x)^2+3)) + c Coefficients (with 95% confidence bounds): a = 23.86 (4.436, 43.29) b = 201.9 (180.2, 223.6) c = 102.9 (93.21, 112.5)Plot the fit and data.
plot(f,angle,counts)
For more details on linear model terms, see the fittype function.