Vereinfachen von Modellen höherer Ordnung

Befehle für die Vereinfachung von Modellen höherer Ordnung

Mit den Befehlen in der folgenden Tabelle können Sie SISO- und MIMO-Modelle niedrigerer Ordnung ableiten.

Befehle für die Vereinfachung von Modellen höherer Ordnung

 
hsvd

Hankel-Einzelwerte eines LTI-Modells berechnen

balred

Approximation eines Modells niedrigerer Ordnung

minreal

Minimalrealisierung (Pol-/Nullstellen-Kompensation)

balreal

Realisierung mit Ausgleich zwischen Eingang/Ausgang berechnen

modred

Zustandslöschung in Realisierung mit E/A-Ausgleich

sminreal

Strukturelle Minimalrealisierung

Techniken für das Vereinfachen von Modellen höherer Ordnung

Zum Verringern der Ordnung eines Modells können Sie eine der folgenden Aktionen ausführen:

  • Mit sminreal die Zustände eliminieren, die strukturell von den Eingängen oder Ausgängen getrennt sind.

    Das Eliminieren der strukturell getrennten Zustände ist ein guter erster Schritt bei der Modellreduktion, da dies ein preiswerter Prozess ist, der ohne numerische Berechnung auskommt.

  • Mit balred eine Approximation niedriger Ordnung Ihres Modells berechnen.

  • Eliminieren Sie sich aufhebende Pol-/Nullstellenpaare mit minreal.

Beispiel: Vergaser-Modell

In diesem Beispiel wird mit einem Modell eines Vergasers gearbeitet. Dies ist ein Gerät, das Feststoffe in Gase umwandelt. Das ursprüngliche Modell ist nichtlinear.

Laden des Modells

Um eine linearisierte Version des Modells zu laden, geben Sie

load ltiexamples

an der MATLAB®-Eingabeaufforderung ein. Das Vergaser-Beispiel ist in der Variable gasf gespeichert. Wenn Sie Folgendes eingeben:

size(gasf)

wird Folgendes zurückgegeben:

Zustandsraummodell mit 4 Ausgängen, 6 Eingängen und 25 Zuständen.

Vereinfachung von SISO-Modellen höherer Ordnung

Sie können die Ordnung eines E/A-Paares verringern, um zu verstehen, wie die Tools für die Modellreduktion funktionieren, bevor Sie versuchen, das vollständige MIMO-Modell zu vereinfachen, wie in Vereinfachung von MIMO-Modellen höherer Ordnung beschrieben.

Dieses Beispiel konzentriert sich auf das Paar aus Eingang 5 und Ausgang 3 des Vergasers.

sys35 = gasf(3,5);

Bevor Sie mit der Reduktion der Modellordnung beginnen, sollten Sie die Positionen der Polstellen/Nullstellen überprüfen, indem Sie Folgendes eingeben:

pzmap(sys35)

Vergrößern Sie einen Bereich in der Nähe des Ursprungs im resultierenden Diagramm. Dazu können Sie die Zoom-Funktion verwenden oder Folgendes eingeben:

axis([-0.2 0.05 -0.2 0.2])

Die folgende Abbildung zeigt die Ergebnisse.

Pol-Nullstellen-Zuordnung des Vergaser-Modells (vergrößert)

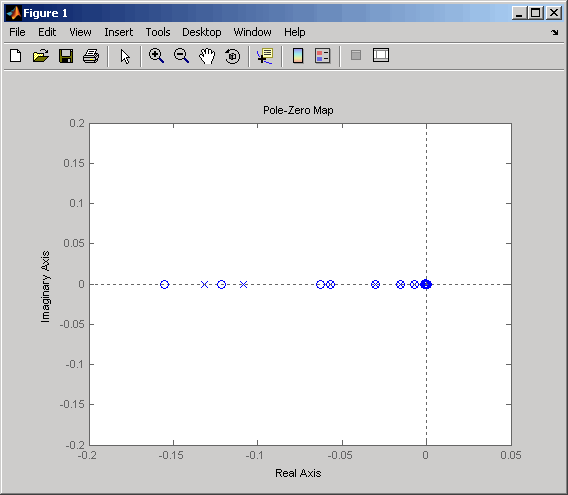
Da im Modell nahe gelegene Pol-Nullstellen-Kompensationen angezeigt werden, ist es ein guter Kandidat für die Modellreduktion.

Um für dieses SISO-Modell eine Vereinfachung niedriger Ordnung zu finden, führen Sie die folgenden Schritte aus:

  1. Wählen Sie eine geeignete Ordnung für Ihr vereinfachtes System aus, indem Sie mit einem Hankel-Singular-Value(HSV)-Diagramm (Hankel-Einzelwert-Diagramm) den relativen Energiebeitrag pro Zustand untersuchen. Geben Sie den folgenden Befehl ein:

    hsvd(sys35)
    um das HSV-Diagramm zu erstellen.

    Wenn Sie das Kontextmenü verwenden, um zur logarithmischen Skala zu wechseln, wird das folgende Diagramm angezeigt.

    Kleine Hankel-Einzelwerte zeigen an, dass die zugehörigen Zustände nur wenig zum E/A-Verhalten beitragen. Dieses Diagramm zeigt, dass das Löschen der letzten 10 Zustände (denen die 10 kleinsten Hankel-Einzelwerte zugeordnet sind) nur wenig Auswirkung auf den Approximationsfehler hat.

  2. Um die letzten 10 Zustände zu entfernen und eine Approximation 15. Ordnung zu erstellen, geben Sie Folgendes ein:

    rsys35 = balred(sys35,15);
    Wenn Sie size(rsys35) eingeben, sehen Sie, dass Ihr vereinfachtes System nur 15 Zustände enthält.

  3. Vergleichen Sie die Bode-Antwort des Modells der Ordnung vor der Modellreduktion und des Modells niedrigerer Ordnung mit dem folgenden „bode“-Befehl:

    bode(sys35,'b',rsys35,'r--')
    Die folgende Abbildung zeigt das Ergebnis.

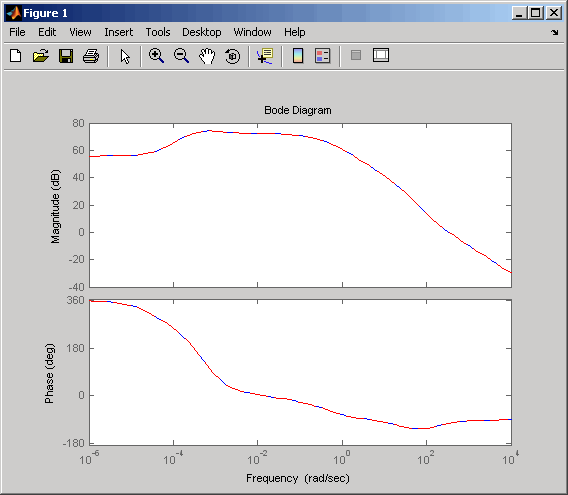
    Wie die Überschneidung der Kurven in der Abbildung zeigt, liefert das vereinfachte Modell eine gute Näherung des ursprünglichen Systems.

Sie können versuchen, die Modellordnung weiter zu verringern, indem Sie diesen Prozess wiederholen und weitere Zustände entfernen. Sie können das Modell gasf gleichzeitig auf die 5., die 10. und die 15. Ordnung vereinfachen, indem Sie den folgenden Befehl eingeben:

rsys35 = balred(sys35,[5 10 15]);
Erstellen Sie ein Bode-Diagramm dieser drei vereinfachten Systeme zusammen mit dem System der Ordnung vor der Vereinfachung, indem Sie Folgendes eingeben:
bode(sys35,'b',rsys35,'r--')

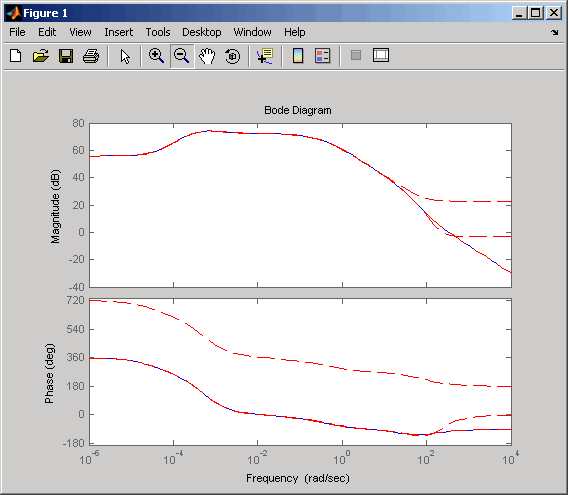
Beobachten Sie, wie mit abnehmender Ordnung der Fehler zunimmt.

Vereinfachung von MIMO-Modellen höherer Ordnung

Für MIMO-Modelle können Sie Näherungen mit denselben Schritten berechnen wie für SISO-Modelle. Gehen Sie also wie folgt vor:

  1. Wählen Sie eine geeignete Ordnung für Ihr vereinfachtes System aus, indem Sie mit einem Hankel-Singular-Value(HSV)-Diagramm (Hankel-Einzelwert-Diagramm) den relativen Energiebeitrag pro Zustand untersuchen.

    Geben Sie Folgendes ein:

    hsvd(gasf)
    um das HSV-Diagramm zu erstellen.

    Das Löschen der letzten 8 Zustände (denen die 8 kleinsten Hankel-Einzelwerte zugeordnet sind) sollte nur wenig Auswirkung auf den Fehler im resultierenden System 17. Ordnung haben.

  2. Um die letzten 8 Zustände zu entfernen und ein MIMO-System 17. Ordnung zu erstellen, geben Sie Folgendes ein:

    rsys=balred(gasf,17);
    Wenn Sie size(gasf) eingeben, sehen Sie, dass Ihr vereinfachtes System nur 17 Zustände enthält.

  3. Um die visuelle Überprüfung des Approximationsfehlers zu erleichtern, sollten Sie statt eines MIMO-Bode-Diagramms ein Einzelwert-Diagramm verwenden. Geben Sie Folgendes ein:

    sigma(gasf,'b',gasf-rsys,'r')
    um ein Einzelwert-Diagramm zum Vergleichen des ursprünglichen Systems mit dem Reduktionsfehler zu erstellen.

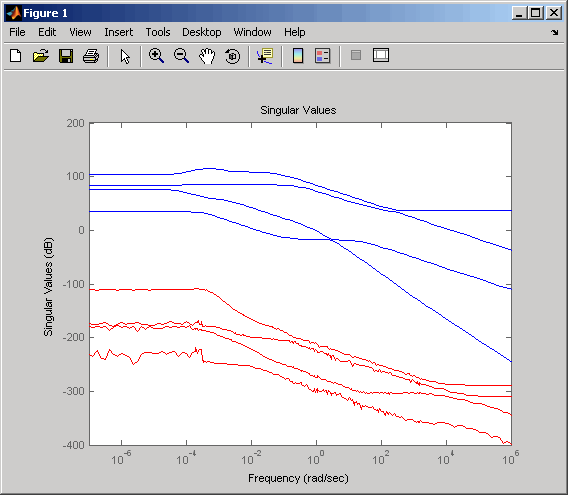
    Im Vergleich zum ursprünglichen System ist der Reduktionsfehler klein. Dies zeigt, dass das vereinfachte Modell eine gute Näherung des ursprünglichen Modells liefert.

Quellenangaben

MathWorks® bedankt sich bei ALSTOM® Power UK für die Erlaubnis, ihr Vergaser-Modell für dieses Beispiel verwenden zu dürfen. Dieses Modell wurde im Rahmen der ALSTOM Benchmark Challenge on Gasifier Control ausgegeben. Weitere Informationen finden Sie in Dixon, R., (1999), „Advanced Gasifier Control“, Computing & Control Engineering Journal, IEE, Bd. 10, Nr. 3, S. 92–96.