berfit
Fit curve to nonsmooth empirical BER data
Syntax
Description
fitber = berfit(empEbNo,empber)empber, and returns a vector of
fitted BER points. The values in empber and fitber
correspond to the empirical energy per bit to noise power spectral density ratio
(Eb/N0)
values given by empEbNo. For a general description of unconstrained
nonlinear optimization, see [1].
Note
The berfit function is intended for curve fitting or
interpolation (not extrapolation). Extrapolating BER data beyond an order of magnitude
below the smallest empirical BER value is inherently unreliable.
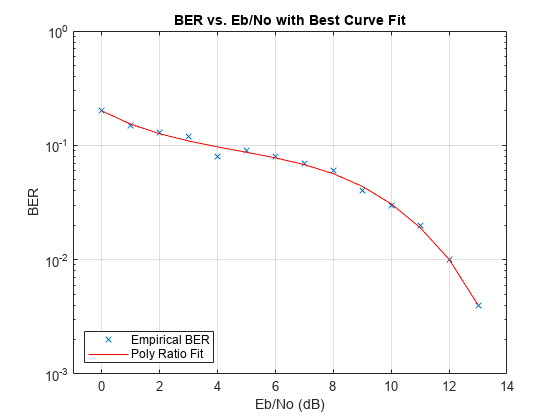
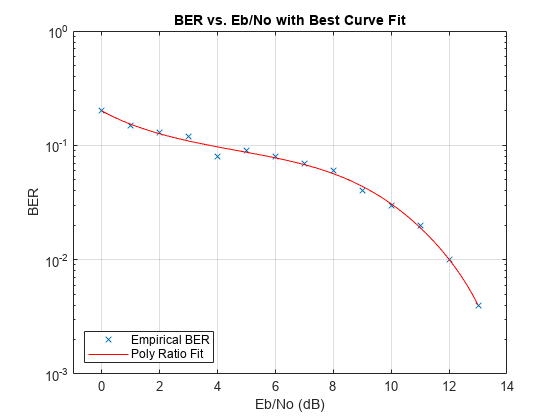
berfit(___) plots the empirical
and fitted BER data.
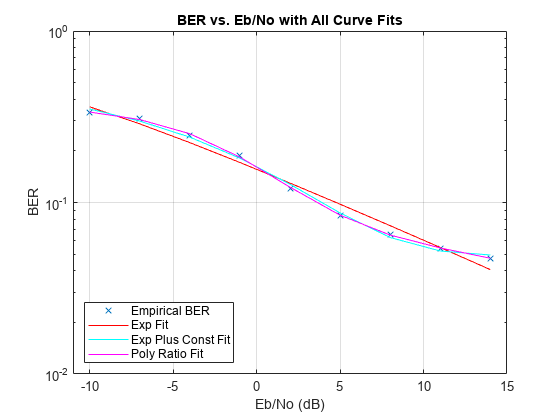
berfit(
plots the empirical and fitted BER data from all possible settings of
empEbNo,empber,fitEbNo,options,'all')fittype that are valid. If you do not want to override the default
options for optimization, specify options as [ ].
Note
To be valid a fit must conform to these criteria, otherwise it is rejected.
real-valued
monotonically decreasing
greater than or equal to 0 and less than or equal to 1
Examples
Input Arguments
Output Arguments
Algorithms
The berfit function fits the BER data using unconstrained nonlinear
optimization via the fminsearch function. This table lists the
closed-form functions that berfit considers based on the value of the
fittype input argument. These functions were empirically found to
provide close fits in a wide variety of situations, including exponentially decaying BERs,
linearly varying BERs, and BER curves with error rate floors. In the functional expressions,
x is a linear
Eb/N0
value (not a dB value), and f(x) is the estimated BER.
fittype Value | Functional Expression |
|---|---|
'exp' |
|
'exp+const' |
|
'polyRatio' |
|
'doubleExp+const' |
|
The sum squared error function that fminsearch attempts to minimize is
The fitted BER points are the values in the output
fitber, and the sum is over the
Eb/N0
points given in the input empEbNo. To avoid high-BER regions dominating
the objective function, the sum squared equation uses the log of the BER values rather than
the BER values themselves.
References
[1] Chapra, Steven C., and Raymond P. Canale. Numerical Methods for Engineers. Fourth Edition. New York, McGraw-Hill, 2002.
Version History
Introduced before R2006a