Die Übersetzung dieser Seite ist veraltet. Klicken Sie hier, um die neueste Version auf Englisch zu sehen.

16-QAM mithilfe von MATLAB untersuchen

Schritt 1 von 3 in BER für QAM-System mit AWGN mithilfe von MATLAB berechnen

Dieses Beispiel veranschaulicht, wie mithilfe einer Kommunikationsverbindung, die aus einem Basisband-Modulator, -Kanal und -Demodulator besteht, ein Datenstrom verarbeitet wird. Im Beispiel werden ein Teil der Zufallsdaten in einem Stamm-Blatt-Diagramm und die übertragenen und die empfangenen Signale in Konstellationsdiagrammen dargestellt und die Bitfehlerrate (Bit Error Rate, BER) berechnet. Informationen zum Hinzufügen eines Impulsformungsfilters zur Kommunikationsverbindung finden Sie im Beispiel Impulsformung bei einem 16-QAM-Signal verwenden. Informationen zum Hinzufügen der Vorwärtsfehlerkorrektur zur Kommunikationsverbindung mit Impulsformfilterung finden Sie im Beispiel Vorwärtsfehlerkorrektur bei einem 16-QAM-Signal verwenden.

Zufallssignal modulieren

Das Modulationsschema verwendet Basisband-16-QAM und das Signal durchläuft einen Additive-White-Gaussian-Noise-(AWGN-)Kanal (AWGN = additives weißes Gaußsches Rauschen). In der Basissimulation verwenden die Operationen die folgenden Communications Toolbox™- und MATLAB®-Funktionen.

rng: Steuert die Generierung von Zufallszahlen
randi: Generiert einen Zufallsdatenstrom
bit2int: Konvertiert die binären Daten in Symbole ganzzahliger Werte
qammod: Moduliert mit 16-QAM
comm.AWGNChannel: Beeinflusst mit AWGN die übertragenen Daten
scatterplot: Erstellt Konstellationsdiagramme
qamdemod: Demoduliert mit 16-QAM
int2bit: Konvertiert die Symbole ganzzahliger Werte in binäre Daten
biterr: Berechnet die BER des Systems

Strom zufälliger binärer Daten generieren

Normalerweise wird ein Signal in MATLAB als Vektor oder Matrix dargestellt. Die Funktion randi erstellt einen Spaltenvektor, der die Werte eines Stroms binärer Daten enthält. Die Länge dieses Binärdatenstroms (also die Anzahl der Zeilen im Spaltenvektor) wird anfänglich auf 30.000 festgelegt.

Definieren Sie die Parameter.

M = 16;      % Modulation order (alphabet size or number of points in signal constellation)
k = log2(M); % Number of bits per symbol
n = 30000;   % Number of bits to process
sps = 1;     % Number of samples per symbol (oversampling factor)

Verwenden Sie die Funktion rng mit ihren Standardeinstellungen oder legen Sie einen statischen Startwert fest, damit das Beispiel wiederholbare Ergebnisse generiert. Verwenden Sie anschließend die Funktion randi, um zufällige binäre Daten zu generieren.

rng default;
dataIn = randi([0 1],n,1); % Generate vector of binary data

Verwenden Sie ein Stamm-Blatt-Diagramm, um die Binärwerte der ersten 40 Bits des Stroms zufälliger binärer Daten anzuzeigen. Verwenden Sie den Doppelpunkt-Operator (:) im Aufruf der Funktion stem, um einen Teil des binären Vektors auszuwählen.

stem(dataIn(1:40),'filled');
title('Random Bits');
xlabel('Bit Index');
ylabel('Binary Value');

Figure contains an axes object. The axes object with title Random Bits contains an object of type stem.

Binäre Daten in Symbole ganzzahliger Werte konvertieren

In der Standardkonfiguration der Funktion qammod wird erwartet, dass die zu modulierenden Eingabesymbole Daten mit ganzzahligem Wert sind. In diesem Beispiel wird der Binärdatenstrom in ganzzahlige Werte konvertiert, bevor die Funktion qammod verwendet wird. Dabei konvertiert die Funktion bit2int jedes 4-Tupel in eine entsprechende ganze Zahl im Bereich [0, (M–1)]. Als Modulationsordnung M wird in diesem Beispiel 16 verwendet.

Führen Sie durch Bestimmung der Anzahl der Bits pro Symbol, die durch $k = l o g_{2} (M)$ definiert ist, eine Bit-zu-Symbol-Zuordnung durch. Verwenden Sie anschließend die Funktion bit2int, um jedes 4-Tupel in einen ganzzahligen Wert zu konvertieren.

dataSymbolsIn = bit2int(dataIn,k);

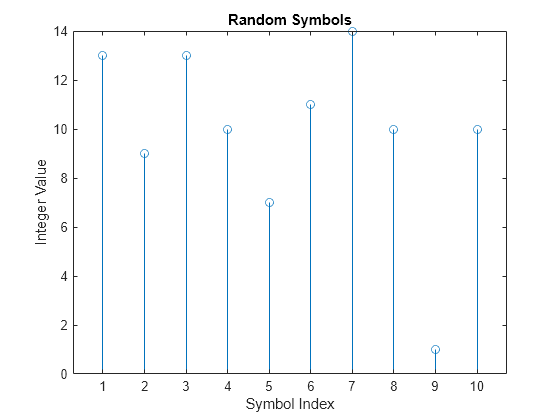
Stellen Sie die ersten 10 Symbole in einem Stamm-Blatt-Diagramm dar.

figure;                    % Create new figure window.
stem(dataSymbolsIn(1:10));
title('Random Symbols');
xlabel('Symbol Index');
ylabel('Integer Value');

Figure contains an axes object. The axes object with title Random Symbols contains an object of type stem.

Mit 16-QAM modulieren

Verwenden Sie die Funktion qammod, um eine 16-QAM-Modulation mit Phasenverschiebung Null auf den Spaltenvektor dataSymbolsIn für binär codierte und Gray-codierte Bit-zu-Symbol-Zuordnungen anzuwenden.

dataMod = qammod(dataSymbolsIn,M,'bin'); % Binary-encoded
dataModG = qammod(dataSymbolsIn,M);      % Gray-encoded

Die Ausgabe der Modulationsoperation sind komplexe Spaltenvektoren mit Werten, die Elemente der 16-QAM-Signalkonstellation sind. Später in diesem Beispiel wird in Konstellationsdiagrammen die Zuordnung der Binär- und Gray-Symbole dargestellt.

Weitere Informationen zu Modulationsfunktionen finden Sie unter Digital Baseband Modulation. Ein Beispiel für die Verwendung der Gray-Codierung mit Phase-Shift-Keying-(PSK-)Modulation (PSK: dt. Phasenumtastung) finden Sie unter Symbol Mapping Examples.

Weißes Gaußsches Rauschen hinzufügen

Das modulierte Signal durchläuft den Kanal unter Verwendung der Funktion awgn mit dem angegebenen Signal-Rausch-Verhältnis (Signal-to-Noise Ratio, SNR). Konvertieren Sie das Verhältnis der Energie pro Bit zur Spektraldichte der Rauschleistung ( $E_{b} / N_{0}$ ) in einen SNR-Wert für die Verwendung durch die Funktion awgn. Die Variable sps ist in diesem Beispiel nicht signifikant, erleichtert aber die zusätzliche Verwendung der Impulsformung im Beispiel. Weitere Informationen finden Sie im Beispiel Impulsformung bei einem 16-QAM-Signal verwenden.

Berechnen Sie das SNR, wenn der Kanal ein $E_{b} / N_{0}$ von 10 dB hat.

EbNo = 10;
snr = EbNo+10*log10(k)-10*log10(sps);

Leiten Sie das Signal für die Zuordnung der binär und Gray-codierten Symbole durch den AWGN-Kanal.

receivedSignal = awgn(dataMod,snr,'measured');
receivedSignalG = awgn(dataModG,snr,'measured');

Konstellationsdiagramm erstellen

Verwenden Sie die Funktion scatterplot, um die gleichphasige Komponente (Wirkkomponente) und die um 90 Grad phasenverschobene Komponente (Blindkomponente) des modulierten Signals dataMod und das mit Rauschen behaftete Signal, das hinter dem Kanal empfangen wurde, anzuzeigen. Die Effekte von AWGN sind im Konstellationsdiagramm dargestellt.

sPlotFig = scatterplot(receivedSignal,1,0,'g.');
hold on
scatterplot(dataMod,1,0,'k*',sPlotFig)

Figure Scatter Plot contains an axes object. The axes object with title Scatter plot contains 2 objects of type line. This object represents Channel 1.

Mit 16-QAM demodulieren

Verwenden Sie die Funktion qamdemod, um die empfangenen Daten zu demodulieren und Datensymbole ganzzahliger Werte auszugeben.

dataSymbolsOut = qamdemod(receivedSignal,M,'bin'); % Binary-encoded data symbols
dataSymbolsOutG = qamdemod(receivedSignalG,M);     % Gray-coded data symbols

Symbole ganzzahliger Werte in binäre Daten konvertieren

Verwenden Sie die Funktion int2bit, um die vom QAM-Demodulator ausgegebenen binär codierten Datensymbole in einen binären Vektor der Länge $(N_{sym} \times N_{bits / sym})$ zu konvertieren. $N_{sym}$ ist die Gesamtzahl der QAM-Symbole und $N_{bits / sym}$ ist die Anzahl der Bits pro Symbol. Für 16-QAM gilt: $N_{bits / sym}$ = 4. Wiederholen Sie diesen Prozess für die Gray-codierten Symbole.

Kehren Sie die Bit-zu-Symbol-Zuordnung, die zuvor in diesem Beispiel durchgeführt wurde, um.

dataOut = int2bit(dataSymbolsOut,k);
dataOutG = int2bit(dataSymbolsOutG,k);

BER des Systems berechnen

Die Funktion biterr berechnet die Bitfehlerstatistiken aus dem ursprünglichen Binärdatenstrom dataIn und den empfangenen Datenströmen dataOut und dataOutG. Bei Gray-Codierung wird die BER beträchtlich verringert.

Verwenden Sie die Fehlerratenfunktion, um die Fehlerstatistiken zu berechnen. Verwenden Sie die Funktion fprintf, um die Ergebnisse anzuzeigen.

[numErrors,ber] = biterr(dataIn,dataOut);
fprintf('\nThe binary coding bit error rate is %5.2e, based on %d errors.\n', ...
    ber,numErrors)

The binary coding bit error rate is 2.27e-03, based on 68 errors.

[numErrorsG,berG] = biterr(dataIn,dataOutG);
fprintf('\nThe Gray coding bit error rate is %5.2e, based on %d errors.\n', ...
    berG,numErrorsG)

The Gray coding bit error rate is 1.63e-03, based on 49 errors.

Signalkonstellationen im Diagramm darstellen

Im zuvor angezeigten Konstellationsdiagramm wurden zwar die Punkte in der QAM-Anordnung dargestellt, die Zuordnung zwischen Symbolwerten und den Konstellationspunkten wurde jedoch nicht angegeben. In diesem Konstellationsdiagramm werden die Zuordnungen für die Binärcodierung und Gray-Codierung der Daten zu Konstellationspunkten angegeben.

Zuordnung der natürlich und Gray-codierten Binärsymbole für 16-QAM-Konstellation anzeigen

Wenden Sie die 16-QAM-Modulation auf vollständige Gruppen aus Konstellationspunkten an, indem Sie die Zuordnung binär codierter Symbole und die Zuordnung Gray-codierter Symbole verwenden.

M = 16;                       % Modulation order
x = (0:15);                   % Integer input
symbin = qammod(x,M,'bin');   % 16-QAM output (binary-coded)
symgray = qammod(x,M,'gray'); % 16-QAM output (Gray-coded)

Verwenden Sie die Funktion scatterplot, um das Konstellationsdiagramm anzuzeigen und mit binär codierten (rot) und Gray-codierten (schwarz) Darstellungen der Konstellationspunkte zu versehen.

scatterplot(symgray,1,0,'b*');
for k = 1:M
    text(real(symgray(k)) - 0.0,imag(symgray(k)) + 0.3, ...
        dec2base(x(k),2,4));
     text(real(symgray(k)) - 0.5,imag(symgray(k)) + 0.3, ...
         num2str(x(k)));
    
    text(real(symbin(k)) - 0.0,imag(symbin(k)) - 0.3, ...
        dec2base(x(k),2,4),'Color',[1 0 0]);
    text(real(symbin(k)) - 0.5,imag(symbin(k)) - 0.3, ...
        num2str(x(k)),'Color',[1 0 0]);
end
title('16-QAM Symbol Mapping')
axis([-4 4 -4 4])

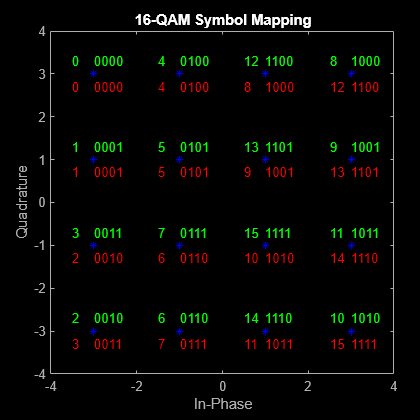
Figure Scatter Plot contains an axes object. The axes object with title 16-QAM Symbol Mapping contains 65 objects of type line, text. This object represents Channel 1.

Diagramme untersuchen

Durch Verwendung der Zuordnung Gray-codierter Symbole verbessert sich die BER-Leistung, da die Gray-codierten Signalkonstellationspunkte um nur ein Bit von jedem benachbarten Punkt abweichen. Bei der Zuordnung binär codierter Symbole weichen dagegen einige der benachbarten Konstellationspunkte um zwei Bits ab. Zum Beispiel weichen die binär codierten Werte für 1 (0 0 0 1) und 2 (0 0 1 0) um zwei Bits (das dritte und das vierte Bit) ab.