Octave-Band and Fractional Octave-Band Filters
This example shows how to design octave-band and fractional octave-band filters, including filter banks and octave SPL meters. Octave-band and fractional-octave-band filters are commonly used in acoustics. For example, octave filters are used to perform spectral analysis for noise control. Acousticians work with octave or fractional (often 1/3) octave filter banks because it provides a meaningful measure of the noise power in different frequency bands.
Octave-Band Filter
An octave is the interval between two frequencies having a ratio of 2:1 (or for base-10 octave ratios). An octave-band or fractional-octave-band filter is a bandpass filter determined by its center frequency, order, and bandwidth. The magnitude attenuation limits are defined in the ANSI® S1.11-2004 standard for three classes of filters: class 0, class 1 and class 2. Class 0 allows only +/-0.15 dB of ripple in the passband, while class 1 allows +/-0.3 dB and class 2 allows +/-0.5 dB. Levels of stopband attenuation vary from 60 to 75 dB, depending on the class of the filter.
Design a full octave-band filter using octaveFilter.
BW = "1 octave"; % Bandwidth N = 8; % Filter order F0 = 1000; % Center frequency (Hz) Fs = 48000; % Sampling frequency (Hz) of = octaveFilter(FilterOrder=N,CenterFrequency=F0, ... Bandwidth=BW,SampleRate=Fs);
Visualize the magnitude response of the filter.
visualize(of,"class 1")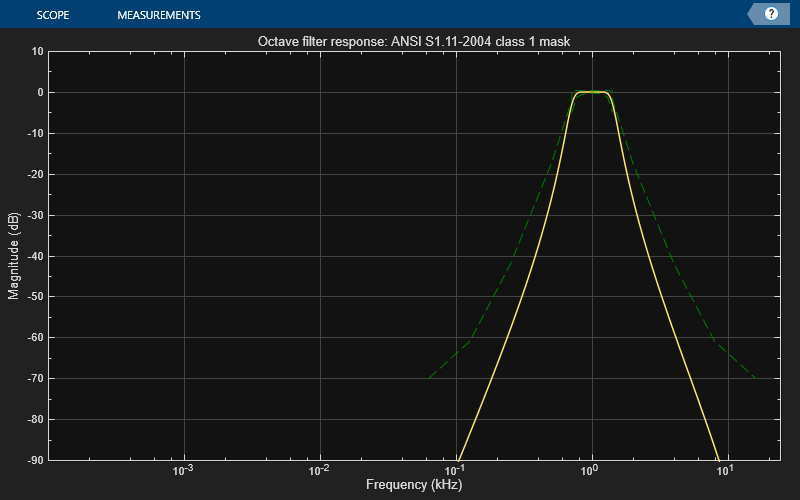
The visualizer plot is synchronized to the object, so you can see the magnitude response update as you change the filter parameters. The mask around the magnitude response is green if the filter complies with the ANSI S1.11-2004 standard (including being centered at a valid frequency), and red otherwise. To change the specifications of the filter with a graphical user interface, use parameterTuner. You can also use the Audio Test Bench app to quickly set up a test bench for the octave filter you designed. For example, run audioTestBench(of) to launch a test bench with octave filter.
Open a parameter tuner that enables you to modify the filter in real time.
parameterTuner(of)
![Figure Audio Parameter Tuner: octaveFilter [of] contains an object of type uigridlayout.](../../examples/audio/win64/OctaveBandAndFractionalOctavebandFilterExample_02.png)
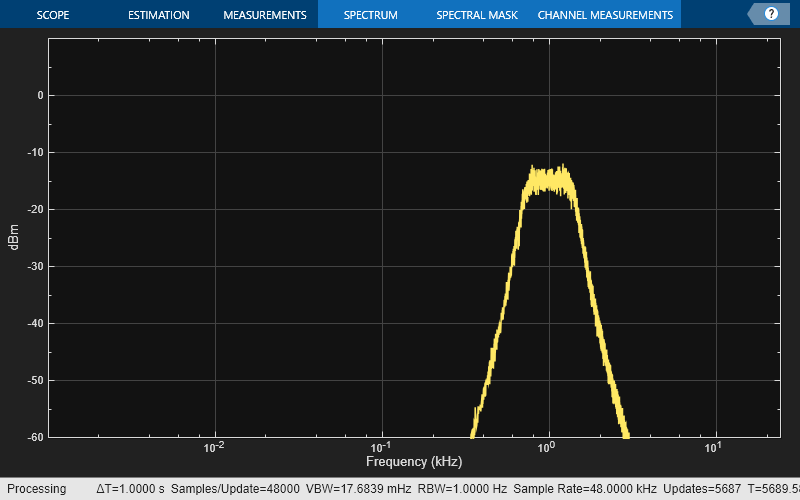
Open a spectrum analyzer to display white noise filtered by the octave filter. You can modify the filter settings with the parameter tuner while the loop runs.
Nx = 100000; scope1 = spectrumAnalyzer(SampleRate=Fs,Method="filter-bank", ... AveragingMethod="exponential",PlotAsTwoSidedSpectrum=false, ... FrequencyScale="log",FrequencySpan="start-and-stop-frequencies", ... StartFrequency=1,StopFrequency=Fs/2,YLimits=[-60 10], ... RBWSource="property",RBW=1); tic while toc < 20 % Run for 20 seconds x1 = randn(Nx,1); y1 = of(x1); scope1(y1) end
Octave-Band Filter Bank
Many applications require a complete set of octave filters to form a filter bank. To design each filter manually, you would use getANSICenterFrequencies(of) to get a list of center frequencies for each individual filter. However, it is usually much simpler to use the octaveFilterBank object.
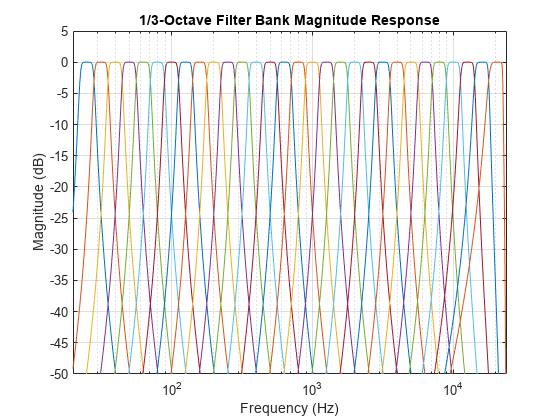
Create an octaveFilterBank object and plot its magnitude response.
ofb = octaveFilterBank("1/3 octave",Fs,FilterOrder=N); freqz(ofb,N=2^16) % Increase FFT length for better low-frequency resolution set(gca,XScale="log") axis([20 Fs/2 -50 5]) title("1/3-Octave Filter Bank Magnitude Response")
Filter the output of a pink noise generator with the 1/3-octave filter bank and compute the total power at the output of each filter.
pinkNoise = dsp.ColoredNoise(Color="pink", ... SamplesPerFrame=Nx, ... NumChannels=1); scope2 = spectrumAnalyzer(SampleRate=Fs,Method="filter-bank", ... AveragingMethod="exponential",PlotAsTwoSidedSpectrum=false, ... FrequencyScale="log",FrequencySpan="start-and-stop-frequencies", ... StartFrequency=20,StopFrequency=Fs/2,YLimits=[-40 30], ... RBWSource="property",RBW=10); centerOct = getCenterFrequencies(ofb); nbOct = numel(centerOct); bandPower = zeros(1,nbOct); nbSamples = 0; tic while toc < 10 xp = pinkNoise(); yp = ofb(xp); bandPower = bandPower + sum(yp.^2,1); nbSamples = nbSamples + Nx; scope2(yp) end

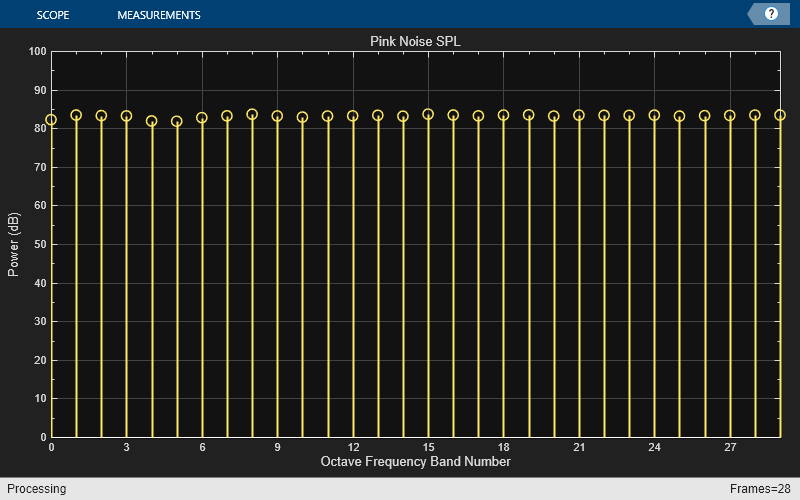
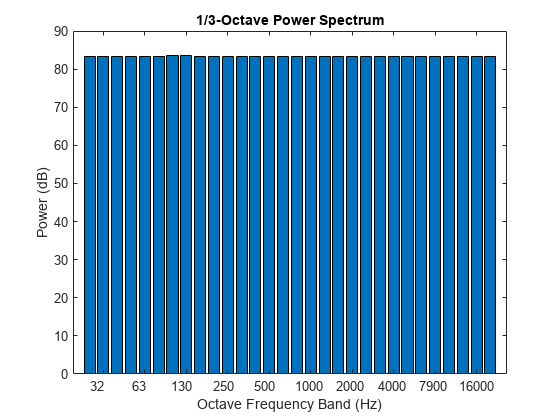
Pink noise has the same total power in each octave band, so the power between 5 Hz and 10 Hz is the same as between 5,000 Hz and 10,000 Hz. Consequently, in the spectrum analyzer, you can observe the 10 dB/decade fall-off that is characteristic of pink noise on a log-log scale, and how that signal is split into the 30 1/3-octave bands. The higher frequency bands have less power density, but the log scale means that they are also wider, so that their total power is constant.
Plot the power spectrum to show that pink noise has a flat octave spectrum.
b = 10^(3/10); % base-10 octave ratio % Compute power (including pressure reference) octPower = 10*log10(bandPower/nbSamples/4e-10); bar(log(centerOct)/log(b),octPower); set(gca,Xticklabel=round(b.^get(gca,"Xtick"),2,"significant")); title("1/3-Octave Power Spectrum") xlabel("Octave Frequency Band (Hz)") ylabel("Power (dB)")
Octave SPL
The SPL Meter object (splMeter) also supports octave-band measurements. Reproduce the same power spectrum measurement in real time. Use a dsp.ArrayPlot object to visualize the power per band. Use the Z-weighting option to omit the frequency weighting filter.
spl = splMeter(Bandwidth="1/3 octave", ... OctaveFilterOrder=N, ... SampleRate=Fs, ... FrequencyWeighting="z-weighting"); scope3 = dsp.ArrayPlot(Title="Pink Noise SPL", ... XLabel="Octave Frequency Band Number", ... YLabel="Power (dB)",YLimits=[0 100]); tic while toc < 10 xp = pinkNoise(); yp = spl(xp); ypm = mean(yp,1).'; scope3(ypm) end