NASA HL-20 Lifting Body Airframe
Introduction
This case study models the airframe of a NASA HL-20 lifting body, a low-cost complement to the Space Shuttle orbiter. The HL-20 is unpowered, but the model includes both airframe and controller.
For most flight control designs, the airframe, or plant model, needs to be modeled, simulated, and analyzed. Ideally, this airframe should be modeled quickly, reusing blocks or model structure to reduce validation time and leave more time available for control design. In this study, the Aerospace Blockset™ software efficiently models portions of the HL-20 airframe. The remaining portions, including calculation of the aerodynamic coefficients, are modeled with the Simulink® software. This case study examines the HL-20 airframe model and touches on how the aerodynamic data are used in the model.
NASA HL-20 Lifting Body
The HL-20, also known as the Personnel Launch System (PLS), is a lifting body reentry vehicle designed to complement the Space Shuttle orbiter. It was developed originally as a low-cost solution for getting to and from low Earth orbit. It can carry up to 10 people and a limited cargo [1].
The HL-20 lifting body can be placed in orbit either by launching it vertically with booster rockets or by transporting it in the payload bay of the Space Shuttle orbiter. The HL-20 lifting body deorbits using a small onboard propulsion system. Its reentry profile is nose first, horizontal, and unpowered.

Top-Front View of the HL-20 Lifting Body (Photo: NASA Langley)

The HL-20 design has a number of benefits:
Rapid turnaround between landing and launch reduces operating costs.
The HL-20 has exceptional flight safety.
It can land conventionally on aircraft runways.
Potential uses for the HL-20 include
Orbital rescue of stranded astronauts
International Space Station crew exchanges
Observation missions
Satellite servicing missions
Although the HL-20 program is not currently active, the aerodynamic data from HL-20 tests are being used in current NASA projects [2].
The HL-20 Airframe and Controller Model
Open the HL-20 airframe and controller model.

Modeling Assumptions and Limitations
Preliminary aerodynamic data for the HL-20 lifting body are taken from NASA document TM4302 [1].
The airframe model incorporates several key assumptions and limitations:
The airframe is assumed to be rigid and have constant mass, center of gravity, and inertia, since the model represents only the unpowered reentry portion of a mission.
HL-20 is assumed to be a laterally symmetric vehicle.
Compressibility (Mach) effects are assumed to be negligible.
Control effectiveness is assumed to vary nonlinearly with angle of attack and linearly with angle of deflection. Control effectiveness is not dependent on sideslip angle.
The nonlinear six-degrees-of-freedom aerodynamic model is a representation of an early version of the HL-20. Therefore, the model is not intended for realistic performance simulation of later versions of the HL-20.
The typical airframe model consists of a number of components, such as
Equations of motion
Environmental models
Calculation of aerodynamic coefficients, forces, and moments
The airframe subsystem of the HL-20 model contains five subsystems, which model the typical airframe components:
6DOF (Euler Angles) Subsystem
The 6DOF (Euler Angles) subsystem contains the six-degrees-of-freedom equations of motion for the airframe. In the 6DOF (Euler Angles) subsystem, the body attitude is propagated in time using an Euler angle representation. This subsystem is one of the equations of motion blocks from the Aerospace Blockset library. A quaternion representation is also available. See the 6DOF (Euler Angles) and 6DOF (Quaternion) block reference pages for more information on these blocks.
Environmental Models Subsystem
The Environmental Models subsystem contains the following subsystems and blocks:
The WGS84 Gravity Model block implements the mathematical representation of the geocentric equipotential ellipsoid of the World Geodetic System (WGS84).
See the WGS84 Gravity Model block reference page for more information on this block.
The COESA Atmosphere Model block implements the mathematical representation of the 1976 Committee on Extension to the Standard Atmosphere (COESA) standard lower atmospheric values for absolute temperature, pressure, density, and speed of sound, given the input geopotential altitude.
See the COESA Atmosphere Model block reference page for more information on this block.
The Wind Models subsystem contains the following blocks:
The Wind Shear Model block adds wind shear to the model.
See the Wind Shear Model block reference page for more information on this block.
The Discrete Wind Gust Model block implements a wind gust of the standard “1 - cosine” shape.
See the Discrete Wind Gust Model block reference page for more information on this block.
The Dryden Wind Turbulence Model (Continuous) block uses the Dryden spectral representation to add turbulence to the aerospace model by passing band-limited white noise through appropriate forming filters.
See the Dryden Wind Turbulence Model (Continuous) block reference page for more information on this block.
The environmental models implement mathematical representations within standard references, such as U.S. Standard Atmosphere, 1976.
Environmental Models in HL-20 Airframe Model

Wind Models in HL-20 Airframe Model

Alpha, Beta, Mach Subsystem
The Alpha, Beta, Mach subsystem calculates additional parameters needed for the aerodynamic coefficient computation and lookup. These additional parameters include
Mach number
Incidence angles (
 )
)Airspeed
Dynamic pressure
The Alpha, Beta, Mach subsystem corrects the body velocity for wind velocity and corrects the body rates for wind angular acceleration.
Additional Computed Parameters for HL-20 Airframe Model (Alpha, Beta, Mach Subsystem)

Aerodynamic Coefficients Subsystem
The Aerodynamic Coefficients subsystem contains aerodynamic data and equations for calculating the six aerodynamic coefficients, which are implemented as in reference [1]. The six aerodynamic coefficients follow.
| Cx | Axial-force coefficient |
| Cy | Side-force coefficient |
| Cz | Normal-force coefficient |
| Cl | Rolling-moment coefficient |
| Cm | Pitching-moment coefficient |
| Cn | Yawing-moment coefficient |
Ground and landing gear effects are not included in this model.
The contribution of each of these coefficients is calculated in the subsystems (body rate, actuator increment, and datum), and then summed and passed to the Forces and Moments subsystem.
Aerodynamic Coefficients in HL-20 Airframe Model

The aerodynamic data was gathered from wind tunnel tests, mainly on scaled models of a preliminary subsonic aerodynamic model of the HL-20. The data was curve fitted, and most of the aerodynamic coefficients are described by polynomial functions of angle of attack and sideslip angle. In-depth details about the aerodynamic data and the data reduction can be found in reference [1].
The polynomial functions contained in the aeroblk_init_hl20.m file are used to calculate lookup tables used by the model's preload function. Lookup tables substitute for polynomial functions. Depending on the order and implementation of the function, using lookup tables can be more efficient than recalculating values at each time step with functions. To further improve efficiency, most tables are implemented as PreLook-up Index Search and Interpolation (n-D) using PreLook-up blocks. These blocks improve performance most when the model has a number of tables with identical breakpoints. These blocks reduce the number of times the model has to search for a breakpoint in a given time step. Once the tables are populated by the preload function, the aerodynamic coefficient can be computed.
The equations for calculating the six aerodynamic coefficients are divided among three subsystems:
Summing the Datum Coefficients, Body Rate Damping, and Actuator Increments subsystem outputs generates the six aerodynamic coefficients used to calculate the airframe forces and moments [1].
Datum Coefficients Subsystem. The Datum Coefficients subsystem calculates coefficients for the basic configuration without control surface deflection. These datum coefficients depend only on the incidence angles of the body.
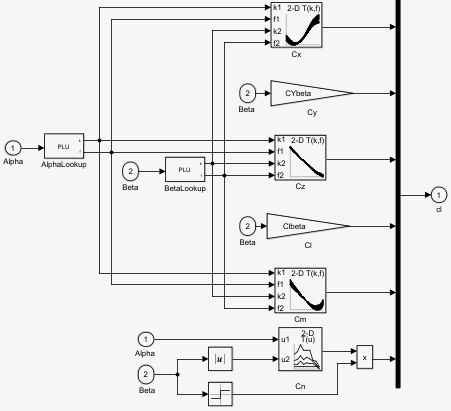
Body Rate Damping Subsystem. Dynamic motion derivatives are computed in the Body Rate Damping subsystem.

Actuator Increment Subsystem. Lookup tables determine the incremental changes to the coefficients due to the control surface deflections in the Actuator Increment subsystem. Available control surfaces include symmetric wing flaps (elevator), differential wing flaps (ailerons), positive body flaps, negative body flaps, differential body flaps, and an all-movable rudder.

Forces and Moments Subsystem. The Forces and Moments subsystem calculates the body forces and body moments acting on the airframe about the center of gravity. These forces and moments depend on the aerodynamic coefficients, thrust, dynamic pressure, and reference airframe parameters.

Complete the Model
These subsystems that you have examined complete the HL-20 airframe. The next step in the
flight control design process is to analyze, trim, and linearize the HL-20 airframe
so that a flight control system can be designed for it. To see an example of an
auto-land flight control for the HL-20 airframe, type the command
openExample('aeroblk_HL20_UE'), at the MATLAB® command line.
References
[1] Jackson, E. B., and C. L. Cruz, “Preliminary Subsonic Aerodynamic Model for Simulation Studies of the HL-20 Lifting Body,” NASA TM4302 (August 1992)..
[2] Morring, F., Jr., “ISS `Lifeboat' Study Includes ELVs,” Aviation Week & Space Technology (May 20, 2002).
