Rekonstruktion eines 3D-Model eines Lithium-Ionen-Akkus in unterschiedlichen Betriebszuständen mithilfe von Neutronencomputertomographie
Von Elmar Tarajan, MathWorks, and Anatoliy Senyshyn, Technische Universität München
Im Unterschied zu Nickel-Cadmium- (NiCd), Nickel-Metallhydrid- (NiMH) oder Bleiakkus bieten Lithium-Ionen-Akkus (Li-Ionen-Akkus) zahlreiche Vorteile zum Speichern elektrochemischer Energie, darunter hohe Energie- und Leistungsdichten, einen vernachlässigbaren Memory-Effekt sowie eine geringe Selbstentladung. Aufgrund dieser Vorteile sind Li-Ionen-Akkus für eine Vielzahl unterschiedlicher Anwendungen ideal geeignet: tragbare Werkzeuge und Unterhaltungselektronik, hybridisiert oder rein elektrisch betriebene Fahrzeuge (vom Fahrrad bis zum Containerschiff) oder stationäre Speicher für erneuerbare Energie aus Wind- oder Solarkraftanlagen zur Netzstabilisierung. Die Li-Ionen-Technologie besitzt jedoch auch Nachteile: So haben Li-Ionen-Akkus auch eine begrenzte Lebensdauer in Bezug auf die erreichbare Zyklenzahl oder die zeitnahe Alterung. Zusätzlich weisen sie einen schmaleren Temperaturbereich auf, in dem ein stabiler Betrieb möglich ist.
Obgleich Forscher aktiv daran arbeiten, diese Schwächen der Li-Ionen-Technologien zu minimieren, werden ihre Bemühungen dadurch erschwert, dass es nicht einfach möglich ist, die komplexen Prozesse, die während des Betriebs im Inneren eines Li-Ionen-Akkus ablaufen, direkt zu beobachten. Moderne Li-Ionen-Akkus sind geschlossene elektrochemische Systeme. Werden Sie zur Untersuchungszwecken geöffnet, kann der vorliegende elektrochemische Gleichgewichtszustand durch Umgebungseinflüsse verfälscht werden.
Um dieses Problem zu umgehen, wenden Forscher unter anderem die Neutronentomographie an, um dreidimensionale (3D) Modelle von Li-Ionen-Akkus zu erstellen [1]. Das 3D-Modell wird aus einer Serie von 2D-Projektionsbildern rekonstruiert, die mittels Neutronenradiographie aufgenommen wurden, einem zerstörungsfreien Bildgebungsverfahren, das Neutronen statt Röntgenstrahlen [2] zur Untersuchung nutzt. In diesem Artikel beschreiben wir den Prozess zur Rekonstruktion eines 3D-Modells eines Li-Ionen-Akkus aus hunderten von radiographischen 2D-Projektionen. Wir benutzen MATLAB® und die Image Processing Toolbox™, um die 2D-Projektions-Bilddateien zu laden, Rauschen zu entfernen, den Rotationsmittelpunkt für jede Projektion zu berechnen, und eine inverse Radon-Transformation durchzuführen, um so final aus den Projektionsdaten einen 3D-Datensatz eines Li-Ionen-Akkus zu erstellen.
Grundlagen der Neutronenradiographie und -tomographie
Andere tomographische Methoden, wie Magnetresonanz-Bildgebung und herkömmliche Röntgen-Bildgebung, weisen Nachteile im Hinblick auf die Li-Ionen-Akkuforschung auf, weil diese Techniken das meist metallische Zellgehäuse nur schwierig oder gar nicht durchdringen können oder aufgrund ihrer physikalischen Wechselwirkung für den Betrieb des Akkus wichtige Bestandteile wie Lithium-, Wasserstoff- und Sauerstoffatome nicht präzise lokalisieren können. Im Gegensatz dazu kann die Neutronenradiographie nicht nur zwischen leichten und benachbarten Elementen im Periodensystem unterscheiden, sondern auch zwischen unterschiedlichen Isotopen. Die Eindringungstiefen sind dabei je nach Energie der Neutronen ausreichend, um den einzelnen Akku oder Akkupacks zu untersuchen.
Ein Neutronenstrahl durchleuchtet dabei das Messobjekt. Je nach Form, Dichte und Isotop-Zusammensetzung des Messobjekts wird der Strahl geschwächt (Abbildung 1). Der Teil der Neutronen, der das Messobjekt passiert, wird als Transmissionssignal mit einem 2D-Detektor gemessen.
Die Anzahl der Projektionen, die bei definierten Winkelpositionen des Messobjekts aufgenommen werden, wird primär durch die Objektgröße und die gewünschte Ortsauflösung bestimmt.
Aus den Projektionen kann eine vollständige 3D-Verteilung der Neutronenschwächungen im Objekt mithilfe eines gefilterten Rückprojektionsalgorithmus zur Berechnung der inversen Radon-Transformation rekonstruiert werden. Dieses Verfahren, die sog. Neutronentomographie, ermöglicht Forschern eine nicht invasive Erstellung von 3D-Darstellungen der Li-Ionen-Akkus und anderer opaker Objekte.
Laden und Vorverarbeitung der Quellbilder/Messdaten
Die von uns bei der Entwicklung der MATLAB-Algorithmen für dieses Projekt verwendeten Daten stammten aus Experimenten [1], die an der Neutron Imaging Beamline ANTARES [2] am Heinz Maier-Leibnitz Zentrum in Garching bei München durchgeführt wurden. Für jeden Datensatz wurden mit einem polychromatischen Neutronenstrahl 600 Projektionen über einen Winkelbereich von 360° aufgenommen, indem der Li-Ionen-Akku für jede Projektion um 0,6° gedreht wurde.
Dies führte zu einem Satz von 2048 x 2048-Pixel-Bildern mit 32-Bit-Auflösung, die unter Einschluss des Rotationswinkels beschriftet wurden. Beispiel:
bat_run1__000.000.fits.tif bat_run1__000.600.fits.tif … bat_run1__359.100.fits.tif bat_run1__359.700.fits.tif
Nach dem Laden jedes Bildes bestand der erste Schritt darin, einen Auswertebereich (Region of Interest, ROI) um den Li-Ionen-Akku herum auszuwählen (Abbildung 2). Hierdurch kann die Gesamtgröße des Tomographiedatensatzes und somit auch die Verarbeitungszeit in den nachfolgenden Schritten stark reduziert werden.
Der folgende MATLAB-Code liest eine einzelne Datei und legt den ROI mithilfe des imrect-Tools fest, das im Abbildungsfenster ein ziehbares Rechteck erzeugt:
>> img = imread('bat_run1__000.000.fits.tif');
>> imshow(img);
>> h = imrect
>> roi = wait(h)
roi =
750 450 650 1600
Danach programmierten wir MATLAB-Code für das Auslesen aller Bilddateien. Um den Prozess zu optimieren und zu beschleunigen, wurde zuvor der Speicher allokiert. Der Rotationswinkel für den Akku (theta) wurde aus jedem Dateinamen extrahiert:
% Determine all available image files file = dir('bat_run1__*.tif'); % Preallocate memory ImageData = zeros(roi(2),roi(1),numel(file)); % Start loop to load images into MATLAB for N1 = 1:numel(file) img = imread(file(N1).name,'PixelRegion',{[roi(2) roi(2)+roi(4)] [roi(1) roi(1)+roi(3)]}); ImageData(:,:,N1) = img; theta(N1) = sscanf(file(N1).name,'bat_run1__%g'); end
Datenvorbereitung
Um die Projektionsdaten und die daraus resultierende Transmissionssignale in Bezug auf Einflüsse der Intensitätsverteilung des Neutronenstrahls und die Nachweiswahrscheinlichkeit des Detektors in den erfassten Bildern zu korrigieren, werden zwei besondere Arten von Referenzbildern verwendet, die zeitnah mit unveränderten experimentellen Parameter erstellt wurden.
Erstens wurde ein Leerbild, auch „openbeam“ oder „flatfield“ genannt, das mit OpenBeamData bezeichnet wird, durch die Durchschnittsbildung mehrerer Bilder des Strahlprofils ohne Messobjekt (kein Akku vorhanden) erstellt, was zu einer praktisch leeren Projektion führt. Zweitens ein Dunkelbild, auch „dark current“ oder „dark image“ genannt, mit DarkFieldData bezeichnet, das durch die Durchschnittsbildung mehrerer Bilder bei abgeschaltetem Neutronenstrahl entstand, was zu einem völlig dunklen Bild führte (Abbildung 3), welches offset-Werte für die einzelnen Pixel des Detektors liegt.
Bei der Neutronentomographie stellen die Intensitätswerte in jedem Projektionsbild die Transmissionseigenschaften des Objekts dar. Die Neutronenschwächung \(μd\) ergibt sich aus \( μd=- ln(\frac{I}{I_0}) \) wobei \(I\) and \(I_0\) jeweils der übertragene bzw. offene Strahl an jedem Pixel sind. Zur Normierung der Projektionen wird das Dunkelbild sowohl von den Projektionsbildern als auch vom Leerbild subtrahiert. Die Normierung der Projektionsdaten und die Berechnung des Neutronenschwächungswerts erfolgt für jedes Projektionsbild mithilfe der folgenden MATLAB-Schleife:
for N1 = 1:numel(file) % remove noise ImageData(:,:,N1) = -log(ImageData(:,:,N1)- DarkFieldData)./(OpenBeamData-DarkFieldData); end
Berechnung des Rotationsmittelpunkts
Bei der inversen Radon-Transformation muss die Objektrotationsachse mit der „Bildmitte“ zusammenfallen. Weil es aber schwierig sein kann, die Objektrotation pixelgenau einzurichten, wird zur Messung eine Grobausrichtung verwendet. Offsets, wie eine Verschiebung und Verkippung, werden später mit MATLAB-Code korrigiert.
Eine Fehlausrichtung des Akkus ist in der Superposition von zwei Bildern offensichtlich, die bei um 180° unterschiedlichen Winkeln erfasst wurden (Abbildung 4).
Um das Ausrichtungs-Offset zu messen, richteten wir ein Optimierungsproblem ein, das den Rotationsmittelpunkt anpasste, um den Unterschied zwischen zwei derartigen Bildern zu minimieren:
function offset = DetermineRotationCentre(img1,img2); offset = fminsearch(@(x) ImageCompare(x,img1,img2),-100); end function f = ImageCompare(x,img1,img2) f=mean(mean(abs(img1-circshift(fliplr(img2),[0 round(x)])))); end
Dann wendeten wir den berechneten Offset auf alle erfassten Bilddaten an:
>> Offset = DetermineRotationCentre(ImageData(:,:,1),ImageData(:,:,301 >> ImageData = ImageData(:,Offset:end,:);
Rekonstruktion des 3D-Volumens aus den Projektionsdaten
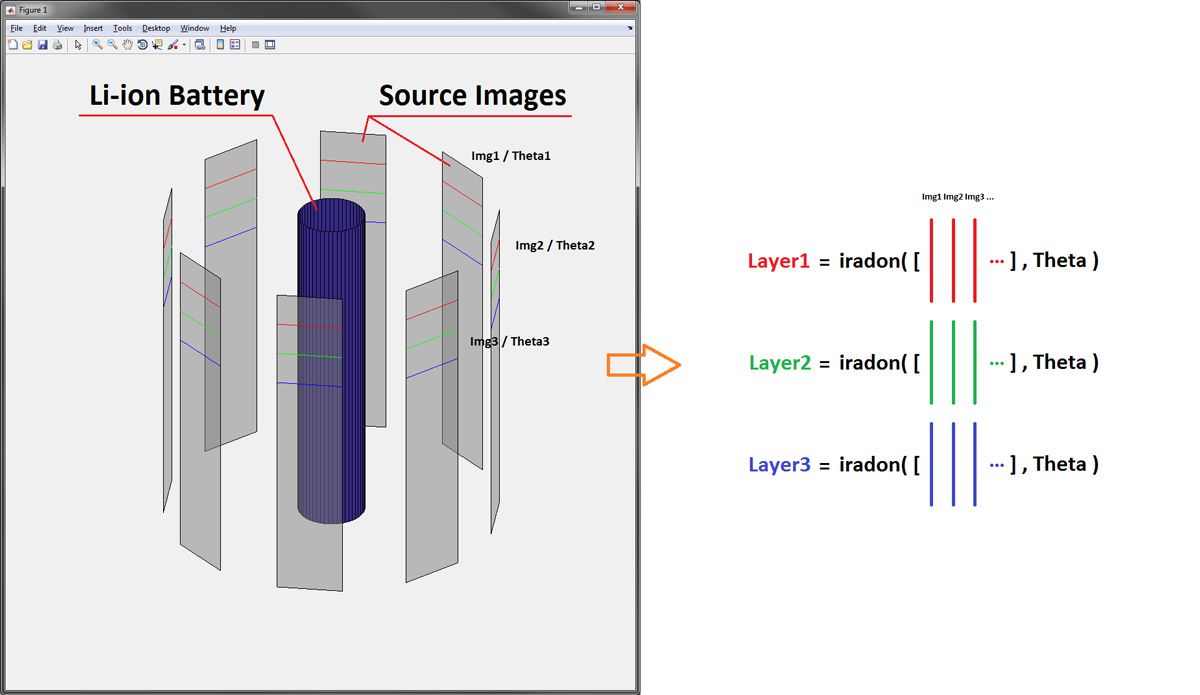
Nachdem die 2D-Bilder geladen, normiert und zentriert wurden, besteht der letzte Schritt zur Rekonstruktion der 3D-Darstellung der Innenstruktur des Akkus in der Durchführung einer inversen Radon-Transformation. Wir nutzten die iradon-Funktion aus der Image Processing Toolbox, um diese Transformation der Projektionsdaten auszuführen und den Li-Ionen-Akku Schicht um Schicht zu rekonstruieren (Abbildung 5).
Die MATLAB-Schleife für die Rekonstruktion des Akkubildes ist recht einfach:
for N1 = 1:size(ImageData,1) % Use squeeze to remove the singleton dimension because iradon expects a 2D-array as an input Layer(:,:,N1) = iradon(squeeze(ImageData(N1,:,:)),Theta); end
Nachdem das Akkubild rekonstruiert wurde, verwendeten wir MATLAB zur Visualisierung einzelner Querschnitte im Detail (Abbildung 6).
Mithilfe des Colormap-Editors wenden wir das Farbschema interaktiv auf die 32-Bit-Schwächungsbilder an (entweder Graustufen oder Falschfarben). Durch die manuelle Anpassung des Farbschemas werden kleine Details wie ein Sicherheitsventil, ein Metallröhrchen im Zentrum, Dichtungen, integrierte Schaltkreise und die Stapelfolge aufgerollter Elektroden des Li-Ionen-Akkus klar sichtbar (Abbildung 7).
Das Ergebnis der Rekonstruktion mit Hilfe der iradon-Funktion liegt als ein 3D-Datenarray vor. Für eine hochwertige Visualisierung der errechneten Daten bietet MATLAB eine Reihe von Funktionen und Möglichkeiten.
Beispiel 1 (Abbildung 8, links)
Mit der isosurface- und patch-Funktion kann das Objekt recht einfach aus dem 3D-Datenarray extrahiert und dargestellt werden:
hFig = figure p = patch( isosurface( Layer, 0.0015, 'colors'), 'FaceColor', [.5 .5 .5], 'EdgeColor', 'none') axis image view(3) grid on lightning phong camlight
Beispiel 2 (Abbildung 8, mitte)
Für die Schnittdarstellung kann die Funktion isocaps herangezogen werden. Dafür „schneiden“ wir ein Teil unserer Daten ab. Danach visualisieren wir zuerst die Außenform und anschließend die Schnittfläche mit Hilfe der isocaps-Funktion:
hFig = figure % Cut off part of the data Layer(1:120,:,:) = []; p1 = patch( isosurface( Layer, 0.0015, 'colors'), 'FaceColor', [.5 .5 .5], 'EdgeColor', 'none') p2 = patch( isocaps( Layer, 0.001), 'FaceColor', 'interp', 'EdgeColor', 'none') axis image view(3) grid on lightning phong camlight
Um auf die rechte Darstellung in der Abbildung 8 zu kommen werden Beispiel 1 und Beispiel 2 nacheinander ausgeführt und die Transparenz der Außenform auf niedrigen Wert gesetzt.
p.FaceAlpha = 0.1;
Der Effekt der Zell-Lade/Entladevorgänge wurde mit einem Neutronentomographie-Experiment untersucht, bei dem die Datenerfassung bei zwei verschiedenen Ladezuständen durchgeführt wurde (Abb. 9), nämlich U=3,00 V (links) und U=4,20 V (rechts), entsprechend dem Ladezustand (SOC) 0 % und 100 %. Die Zelle wurde während der Datenerfassung nicht erneut montiert, experimentelle Details und Expositionszeit pro Projektion wurden gleich gewählt, was den direkten Vergleich der an verschiedenen SOCs gesammelten Datensätze ermöglicht. Bei der Farbcodierung, die einheitlich auf die erfassten Daten angewendet wurde, entspricht die blaue Farbe einer geringen Neutronenschwächung. Die sich ändernde Farbe bis hin zu Rot zeigt Bereiche mit zunehmender Neutronenschwächung anzeigt.
Bei SOC=0 % wurden die gut aufgelösten Elektrodenschichten beobachtet. Beim Aufladen der Zelle auf 4,0 V ist der Kontrast zwischen den Schichten reduziert und im vollgeladenen Zustand (bei 4,2 V) sind keine unterschiedlichen Elektrodenschichten zu sehen. Das beobachtete ladungsbedingte "Verschwinden" von Elektrodenschichten lässt sich darauf zurückführen, dass sich bei SOC nahe 0 % der Großteil des Lithiums an der negativen Elektrode (Kathode) befindet. Die Zellaufladung zwingt Lithium dazu, sich von der Kathode zur Anode zu bewegen, wodurch der anfängliche Kontrast zwischen den positiven und negativen Elektroden reduziert wird und die Schichtung in den rekonstruierten Bildern verschwindet. Aufgrund seiner besonderen Eigenschaften lässt sich Lithium in den Batterien ausgezeichnet mit neutronenbasierten Bildgebungsverfahren erkennen, Übergangselemente von der Kathode oder Stromzuleitung unterscheiden sowie die Elektrodendynamik durch Wasserstoff-Lokalisierung überwachen.
Schlussfolgerungen
Das von uns in MATLAB implementierte Rekonstruktionsverfahren bietet eine zerstörungsfreie Methode zur Beobachtung des Verhaltens des Li-Ionen-Akkubetriebs unter verschiedenen Bedingungen und Alterungszuständen. Diese Aspekte machen das Verfahren zu einem hocheffektiven Diagnosewerkzeug. Es ist besonders gut für die in-situ-Alterungsdiagnose geeignet, die als Teil der Qualitätskontrolle bei der Akkuherstellung implementiert werden kann. Der von uns verwendete MATLAB-Code kann durch die Implementierung weiterer zusätzlicher Datenfiltrierungstechniken oder durch weitere Visualisierungsansichten des rekonstruierten 3D-Bildes beliebig erweitert und auf einfache Weise angepasst werden.
Danksagungen
Der experimentelle Teil des Projekts wurde von der Deutschen Forschungsgemeinschaft unterstützt. Wir danken dem Heinz Maier-Leibnitz Zentrum für den Zugang zur experimentellen Infrastruktur.
Veröffentlicht 2017 - 93174v00
Literatur
-
A. Senyshyn, M.J. Mühlbauer, K. Nikolowski, T. Pirling, and H. Ehrenberg, "'In-operando' neutron scattering studies on Li-ion batteries," J. Power Sources 203 (2012) 126-129.
-
Heinz Maier-Leibnitz Zentrum (2015), "ANTARES: Cold neutron radiography and tomography facility," Journal of large-scale research facilities, 1, A17. http://jlsrf.org/index.php/lsf/article/view/42