Second generation Vold-Kalman Order Filtering
The Vold-Kalman Filter, introduced by Håvard Vold and Jan Leuridan in 1993, is able to extract non-stationary periodic components from a signal using a known frequency vector [1]. Being formulated in a least-squares sense, it can be solved as a sparse linear system. Similar to the Kalman filter, VKF minimises a cost function based on a structural equation and a data equation.
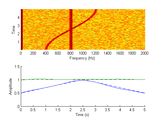
This submission implements the second generation VKF with the ability to extract multiple orders at the same time, with energy spreading in case of crossing orders [2].
Syntax:
x = vkf(y,fs,f) extracts the order with frequency vector f from signal y with samplerate fs, using a 2-pole filter with a -3dB bandwidth of 1 percent of the sample rate. The output is a single waveform x.
[...] = vkf(y,fs,f,p) uses a p-order filter (typically between 1 or 4). Every order increases the roll-off by -40dB per decade. By specifying additional lower-order coefficients, zero boundary conditions are added. For instance: p = [2 0 1] applies 2nd order filtering and forces the envelope amplitude and its first derivative to zero at t_1 and t_N.
[...] = vkf(y,fs,f,p,bw) uses a bandwidth in Hertz specified by bw. If bw is a scalar, a constant bandwidth is used; if bw is a vector with the same length as y, a time-varying instantaneous bandwidth is realised.
X = vkf(y,fs,F,...) with [N,K] = size(F), performs simultaneous extraction of K orders with frequency vectors [f_1,...,f_K] in array F. In case of crossing orders, this method tries to reveal the correctorder amplitudes. The output is an array of K waveforms [x_1,...,x_K].
X = vkf(y,fs,F,p,bw,0) switches to a single-order algorithm. K orders are still extracted, but the single-order algorithm is computationally less demanding. This is suggested for high sample rates and/or long timeseries.
[a,c] = vkf(...) returns the complex envelope(s) a and phasor(s) c, such that the order waveform(s) can be reconstructed by x = real(a.*c).
[a,c,r] = vkf(...) ouputs an additional selectivity vector r used to realise the bandwidth given by bw.
Demo:
Calling VKF without arguments shows a small demonstration of multi-order filtering with two crossing orders in the presence of white noise.
Note: Filter orders > 4 usually result in ill conditioning and should be avoided. The filter bandwidth determination was implemented for arbitrary order but was not verified for orders higher than 3.
Written by: Maarten van der Seijs, 2010.
Version 1.4, 3 May 2013.
References:
[1] Vold, H. and Leuridan, J. (1993), High resolution order tracking at extreme slew rates, using Kalman tracking filters. Technical Report 931288, Society of Automotive Engineers.
[2] Tuma, J. (2005), Setting the passband width in the Vold-Kalman order tracking filter. Proceedings of the International Congress on Sound and Vibration (ICSV12), Lisbon, Portugal.
Zitieren als
Maarten van der Seijs (2024). Second generation Vold-Kalman Order Filtering (https://www.mathworks.com/matlabcentral/fileexchange/36277-second-generation-vold-kalman-order-filtering), MATLAB Central File Exchange. Abgerufen .
Kompatibilität der MATLAB-Version
Plattform-Kompatibilität
Windows macOS LinuxKategorien
- Test and Measurement > Data Acquisition Toolbox > Periodic Waveform Generation >
- Signal Processing > Signal Processing Toolbox > Signal Generation and Preprocessing > Waveform Generation >
- Control Systems > Control System Toolbox > Linear Analysis > Stability Analysis > Pole and Zero Locations >
Tags
Community Treasure Hunt
Find the treasures in MATLAB Central and discover how the community can help you!
Start Hunting!Live Editor erkunden
Erstellen Sie Skripte mit Code, Ausgabe und formatiertem Text in einem einzigen ausführbaren Dokument.
| Version | Veröffentlicht | Versionshinweise | |
|---|---|---|---|
| 1.7.0.0 | now with new m-file |
||
| 1.4.0.0 | Bug update for single-order algorithm. |
||
| 1.3.0.0 | Minor changes to description and code. Functionally the same. |
||
| 1.0.0.0 |