Die Übersetzung dieser Seite ist veraltet. Klicken Sie hier, um die neueste Version auf Englisch zu sehen.

Neues Wavelet für CWT

In diesem Beispiel wird erläutert, wie Sie ein neues Wavelet beginnend bei einem Muster generieren.

Das Prinzip der Entwicklung eines neuen Wavelets für CWT besteht darin, eine Approximation für ein bestimmtes Muster mithilfe der Optimierung der kleinsten Quadrate unter Einschränkungen vorzunehmen. Das Ergebnis ist ein zulässiges Wavelet, das gut für die Mustererkennung mithilfe der kontinuierlichen Wavelet-Transformation geeignet ist [1].

Laden Sie ein Originalmuster: einen Pseudo-Sinus.

load ptpssin1
who

Your variables are:

IntVAL   X        Y        caption  

Die Variablen X und Y enthalten das Muster. Integrieren Sie das Muster über dem Intervall [0, 1]. Plotten Sie das Muster.

dX = max(diff(X));
patternInt = dX*sum(Y);
disp(['Integral of pattern = ',num2str(patternInt)]);

Integral of pattern = 0.15915

plot(X,Y)
title('Original Pattern')
grid on

Das Muster über dem Intervall [0, 1] wird bei 0,15915 integriert. Daher ist es kein Wavelet, jedoch ein guter Kandidat dafür, da es wie ein Wavelet oszilliert.

Um ein neues Wavelet zu synthetisieren, das an ein bestimmtes Muster angepasst wurde, verwenden Sie eine Polynom-Approximation der kleinsten Quadrate und des Grades 6 mit Kontinuitätseinschränkungen am Anfang und Ende des Musters.

[psi,xval,nc] = pat2cwav(Y, 'polynomial',6, 'continuous');

Das neue Wavelet entsteht durch xval und nc*psi.

figure
plot(X,Y,'-',xval,nc*psi,'--')
grid on
legend('Original Pattern','Adapted Wavelet','Location','NorthWest')

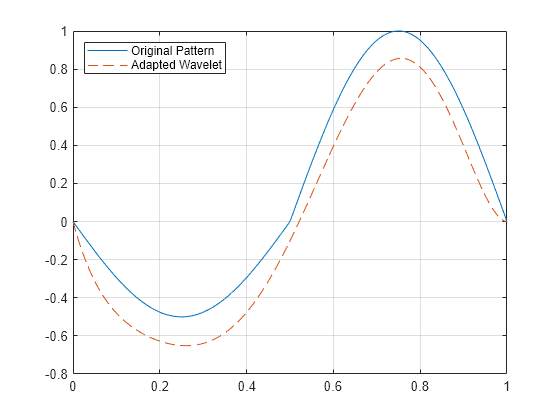
Vergewissern Sie sich, ob psi der Definition eines Wavelets entspricht, indem Sie prüfen, ob es bei 0 integriert und eine $$L_2$$-Norm aufweist, die 1 entspricht.

dxval = max(diff(xval));
newWaveletIntegral = dxval*sum(psi);
disp(['Integral of new wavelet = ',num2str(newWaveletIntegral)])

Integral of new wavelet = 1.9626e-05

newWaveletSqN = dxval*sum(psi.^2);
disp(['New wavelet has L2-norm = ',num2str(newWaveletSqN)])

New wavelet has L2-norm = 1

Referenzen

[1] Misiti, M., Y. Misiti, G. Oppenheim, and J.-M. Poggi. Les ondelettes et leurs applications. France: Hermes Science/Lavoisier, 2003.

Siehe auch

pat2cwav