Die Übersetzung dieser Seite ist veraltet. Klicken Sie hier, um die neueste Version auf Englisch zu sehen.

Lifting

Dieses Beispiel zeigt die Anwendung von Lifting auf ein 1D-Signal.

Erzeugen Sie ein 1D-Signal, das über 2 Abtastwerte stückweise konstant ist. Fügen Sie dem Signal folgendes Rauschen hinzu: $$N(0,0.1^2)$$.

x = [1 1 2 2 -3.5 -3.5 4.3 4.3 6 6 -4.5 -4.5 2.2 2.2 -1.5 -1.5];
x = repmat(x,1,64);
rng default
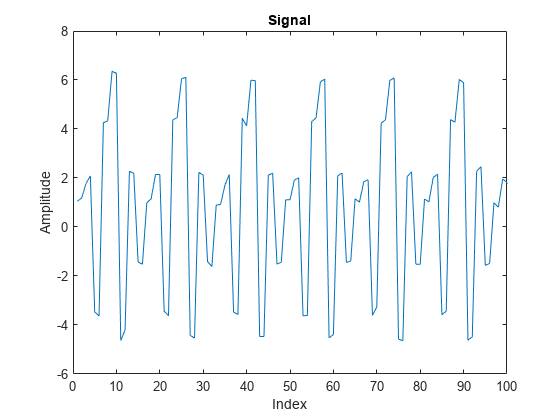
x = x+ 0.1*randn(size(x));

Stellen Sie das Signal grafisch dar und vergrößern Sie die ersten 100 Abtastwerte, um die Korrelation in benachbarten Abtastwerten zu visualisieren.

plot(x)
xlim([0 100])
title('Signal')
xlabel('Index')
ylabel('Amplitude')

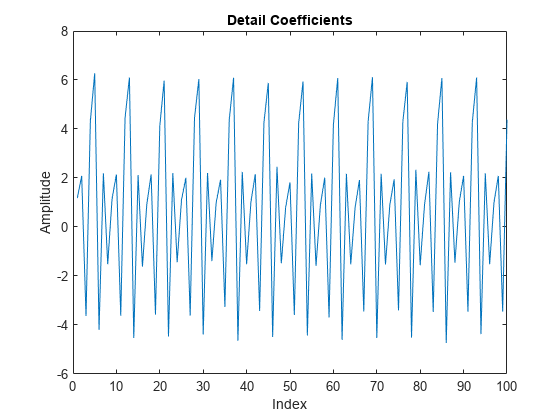
Verwenden Sie das Lazy-Wavelet, um die geraden und ungeraden Mehrphasenkomponenten des Signals zu ermitteln. Stellen Sie die Detailkoeffizienten (Wavelet-Koeffizienten) in D grafisch dar. Sie werden feststellen, dass diese Transformation das Signal nicht dekorreliert hat. Die Wavelet-Koeffizienten sehen dem Signal sehr ähnlich.

LS = liftingScheme;
[A,D] = lwt(x,'LiftingScheme',LS,'Level',1);
plot(D{1})
xlim([0 100])
title('Detail Coefficients')
xlabel('Index')
ylabel('Amplitude')

Fügen Sie einen Prädiktions-Lifting-Schritt hinzu, der den geradzahligen Koeffizienten vom ungeradzahligen Koeffizienten des unmittelbar folgenden Abtastwerts subtrahiert: $$x(2n+1)-x(2n)$$.

ElemLiftStep = liftingStep('Type','predict','Coefficients',-1,'MaxOrder',0);
LSnew = addlift(LS,ElemLiftStep);

Da das Signal über aufeinanderfolgende Abtastwerte mit additivem Rauschen stückweise konstant ist, sollte der neue Prädiktionsschritt in Wavelet-Koeffizienten mit kleinem Absolutwert resultieren. In diesem Fall dekorreliert die Wavelet-Transformation die Daten. Verifizieren Sie dies, indem Sie die Approximations- und Detailkoeffizienten mit dem neuen Prädiktionsschritt ermitteln.

[A,D] = lwt(x,'liftingScheme',LSnew,'Level',1);

Wenn Sie die Detailkoeffizienten (Wavelet-Koeffizienten) grafisch darstellen, sehen Sie, dass die Wavelet-Koeffizienten dem Originalsignal nicht mehr ähneln.

plot(D{1})
xlim([0 100])
title('Detail Coefficients')
xlabel('Index')
ylabel('Amplitude')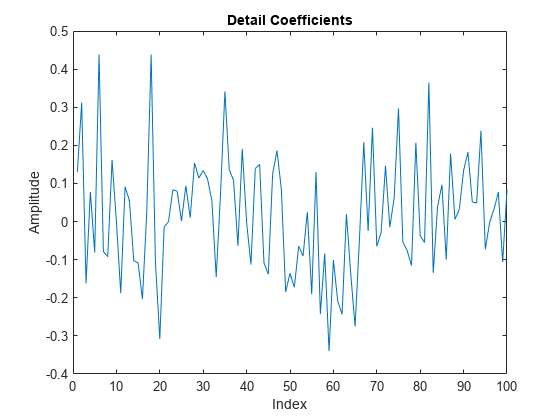

Die Approximationskoeffizienten A der vorherigen Transformation bilden die gerade Mehrphasenkomponente des Signals. Daher sind die Koeffizienten von Aliasing betroffen. Verwenden Sie einen Update-Lifting-Schritt, um die Approximationskoeffizienten zu aktualisieren und Aliasing zu reduzieren. Der Update-Schritt ersetzt die Approximationskoeffizienten durch $$x(2n)+1/2(x(2n+1)-x(2n))$$. Dies ist gleich dem Mittelwert von $$x(2n)$$ und $$x(2n+1)$$. Die Mittelwertbildung ist eine Tiefpassfilterung, die dazu beiträgt, Aliasing zu reduzieren.

ElemLiftStep = liftingStep('Type','update','Coefficients',1/2,'MaxOrder',0);
LSnew = addlift(LSnew,ElemLiftStep);

Verwenden Sie das neue Lifting-Schema, um die Wavelet-Transformation des Eingangssignals zu erhalten. Die Approximationskoeffizienten ähneln einer geglätteten Version des Originalsignals.

[A,D] = lwt(x,'liftingScheme',LSnew,'Level',1);
plot(A)
xlim([0 100])

Erstellen Sie ein neues Lifting-Schema mit den gleichen Lifting-Schritten wie in LSnew. Wenden Sie Skalierungsfaktoren an, um eine perfekte Rekonstruktion sicherzustellen. Ermitteln Sie die Approximations- und Wavelet-Koeffizienten mithilfe des Lifting-Schemas und rekonstruieren Sie das Signal mithilfe von ilwt. Verifizieren Sie, dass die Rekonstruktion perfekt ist.

scaleFactors = [sqrt(2) sqrt(2)/2];
ElemLiftStep1 = liftingStep('Type','predict','Coefficients',-1,'MaxOrder',0);
ElemLiftStep2 = liftingStep('Type','update','Coefficients',1/2,'MaxOrder',0);
LSscale = liftingScheme('LiftingSteps',[ElemLiftStep1;ElemLiftStep2], ...
    'NormalizationFactors',scaleFactors);
[A,D] = lwt(x,'liftingScheme',LSscale,'Level',1);
xrecon = ilwt(A,D,'liftingScheme',LSscale);
max(abs(x(:)-xrecon(:)))

ans = 1.7764e-15

Im vorstehenden Beispiel wurde ein Wavelet entwickelt, das ein Polynom nullter Ordnung (Konstante) effektiv entfernt. Wenn das Verhalten des Signals durch ein Polynom höherer Ordnung besser dargestellt wird, können Sie ein duales Wavelet mit der entsprechenden Anzahl von verschwindenden Momenten entwickeln, um das Signal zu dekorrelieren.

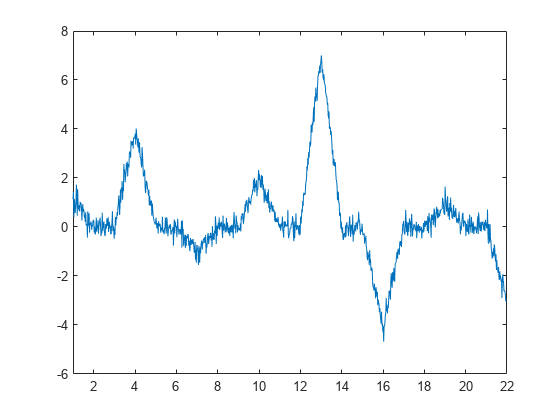
Verwenden Sie das Lifting-Schema, um ein Wavelet mit zwei verschwindenden Momenten zu entwickeln. Ein duales Wavelet mit zwei verschwindenden Momenten dekorreliert ein Signal mit lokalem Verhalten, das durch ein Polynom erster Ordnung approximiert wird. Erstellen Sie ein durch ein Polynom erster Ordnung gekennzeichnetes Signal mit additivem Rauschen: $$N(0,0.25^2)$$.

y = [1 0 0 4 0 0 -1 0 0 2 0 0 7 0 0 -4 0 0 1 0 0 -3];
x1 = 1:(21/1024):22-(21/1024);
y1 = interp1(1:22,y,x1,'linear');
rng default
y1 = y1+0.25*randn(size(y1));
plot(x1,y1)
xlim([1 22])

In diesem Fall sollten die Wavelet-Koeffizienten ein Polynom erster Ordnung entfernen. Wenn der Signalwert bei einem ungeraden Index, $$x(2n+1)$$, durch ein Polynom erster Ordnung, das an die umgebenden Abtastwerte angepasst ist, gut approximiert wird, sollte $$1/2(x(2n)+x(2n+2))$$ eine gute Anpassung für $$x(2n+1)$$ liefern. Anders ausgedrückt, $$x(2n+1)$$ sollte der Mittelpunkt zwischen $$x(2n)$$ und $$x(2n+2)$$ sein.

Daraus folgt, dass $$x(2n+1)-1/2(x(2n)+x(2n+2))$$ das Signal dekorrelieren sollte.

Erstellen Sie ein neues Lifting-Schema mit dem Prädiktions-Lifting-Schritt, der die vorhergehende Gleichung modelliert.

ElemLiftStep = liftingStep('Type','predict','Coefficients',[-1/2 -1/2],'MaxOrder',1);
LS = liftingScheme('LiftingSteps',ElemLiftStep,'NormalizationFactors',1);

Ermitteln Sie die Approximations- und Detailkoeffizienten mithilfe des Lifting-Schemas und stellen Sie das Ergebnis grafisch dar.

[A,D] = lwt(y1,'LiftingScheme',LS,'Level',1);
subplot(2,1,1)
plot(A)
xlim([1 512])
title('Approximation Coefficients')
subplot(2,1,2)
plot(D{1})
xlim([1 512])
title('Detail Coefficients')

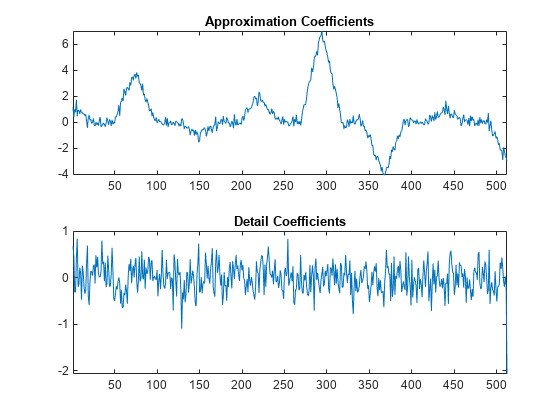
Die Wavelet-Koeffizienten scheinen nur Rauschen zu enthalten, während die Approximationskoeffizienten eine entrauschte Version des Originalsignals darstellen. Da in der vorhergehenden Transformation nur die gerade Mehrphasenkomponente für die Approximationskoeffizienten verwendet wird, können Sie Aliasing durch Hinzufügen eines Update-Schritts reduzieren.

Erstellen Sie ein neues Lifting-Schema, das aus dem vorherigen Prädiktionsschritt und einem neuen Update-Schritt besteht, der Aliasing reduziert. Normalisieren Sie das Lifting-Schema, um eine perfekte Rekonstruktionsfilterbank zu erzeugen. Ermitteln Sie die diskrete Wavelet-Transformation mit dem neuen Lifting-Schema, und stellen Sie die Ergebnisse grafisch dar.

scaleFactors = [sqrt(2) sqrt(2)/2];
ElemLiftStep1 = liftingStep('Type','predict','Coefficients',[-1/2 -1/2],'MaxOrder',1);
ElemLiftStep2 = liftingStep('Type','update','Coefficients',[1/4 1/4],'MaxOrder',0);
LSnew = liftingScheme('LiftingSteps',[ElemLiftStep1;ElemLiftStep2], ...
    'NormalizationFactors',scaleFactors);
[A,D] = lwt(y1,'liftingScheme',LSnew,'Level',1);
subplot(2,1,1)
plot(A)
xlim([1 512])
title('Approximation Coefficients')
subplot(2,1,2)
plot(D{1})
xlim([1 512])
title('Detail Coefficients')

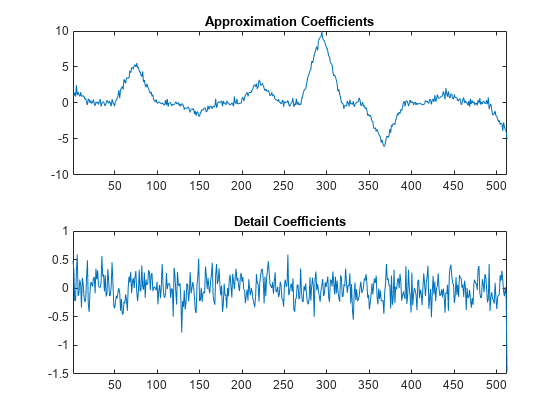
Demonstrieren Sie, dass Sie eine perfekte Rekonstruktionsfilterbank entwickelt haben.

y2 = ilwt(A,D,'liftingScheme',LSnew);
max(abs(y2(:)-y1(:)))

ans = 1.7764e-15

Siehe auch

liftingScheme | liftingStep

Verwandte Themen

• Lifting Method for Constructing Wavelets