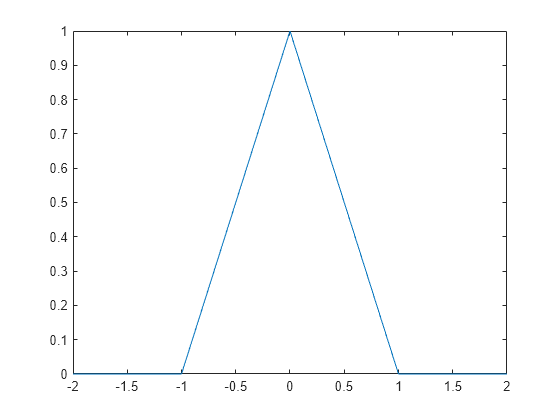
triangularPulse
Triangular pulse function
Description
Examples
Input Arguments
More About
Tips
If
a,b, andcare variables or expressions with variables,triangularPulseassumes thata <= b <= c. Ifa,b, andcare numerical values that do not satisfy this condition,triangularPulsethrows an error.If
a = b = c,triangularPulsereturns 0.If
a = borb = c, the triangular function can be expressed in terms of the rectangular function.
Version History
Introduced in R2012b