postFitStatistics
Compute post-fit statistics for the exact Gaussian process regression model
Syntax
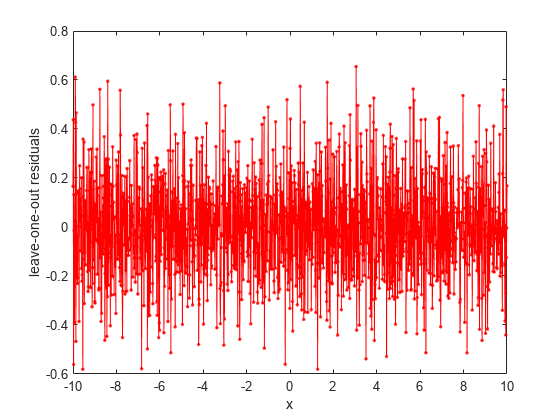
loores = postFitStatistics(gprMdl)
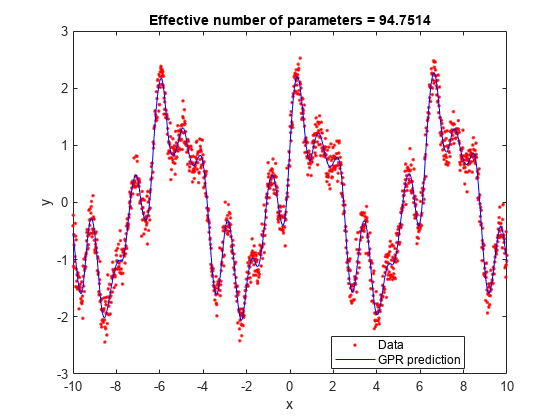
[loores,neff] = postFitStatistics(gprMdl)
Description
Input Arguments
Output Arguments
Examples
Tips
You can only compute the post-fit statistics when
PredictMethodis'exact'.If
FitMethodis'exact', thenpostFitStatisticsaccounts for the fact that the fixed basis function coefficients are estimated from the data.If
FitMethodis different than'exact', thenpostFitStatisticstreats the fixed basis function coefficients as known.For all
PredictMethodandFitMethodoptions,postFitStatisticstreats the estimated kernel parameters and noise standard deviation as known.
Version History
Introduced in R2015b