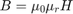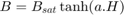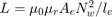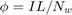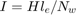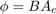Nonlinear Inductor Characteristics
This example shows a comparison of nonlinear inductor behavior for different parameterizations. Starting with fundamental parameter values, the parameters for linear and nonlinear representations are derived. These parameters are then used in a Simscape™ model and the simulation outputs compared.
Specification of Parameters
Fundamental parameter values used as the basis for subsequent calculations:
Permeability of free space,

Relative permeability of core,

Number of winding turns,
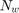
Effective magnetic core length,

Effective magnetic core cross-sectional area,
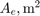
Core saturation begins,

Core fully saturated,

Calculate Magnetic Flux Density and Magnetic Field Strength Data
Where:
Magnetic flux density,

Magnetic field strength,
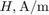
Linear representation:
Nonlinear representation (including coefficient, a):
Display Magnetic Flux Density Versus Magnetic Field Strength
The linear and nonlinear representations can be overlaid.
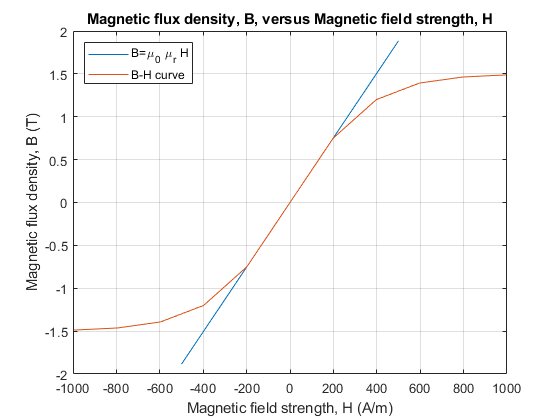
Calculate Magnetic Flux and Current Data
Where:
Magnetic flux,
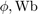
Current,
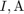
Linear representation:
Nonlinear representation:
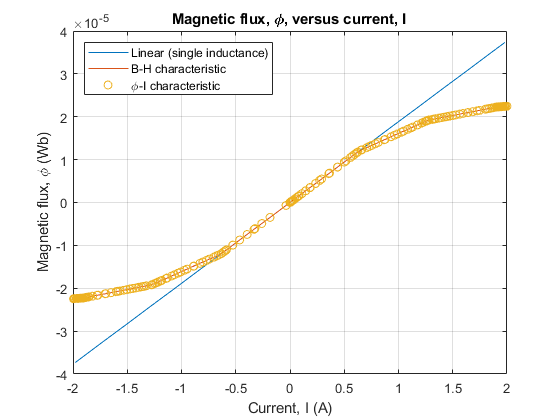
Display Magnetic Flux Versus Current
The linear and nonlinear representations can be overlaid.

Use Parameters in Simscape Model
The parameters calculated can now be used in a Simscape model. Once simulated, the model is set to create a Simscape logging variable, simlog.

Conclusion
The state variable for all representations is magnetic flux,  . Current, I, and magnetic flux,
. Current, I, and magnetic flux,  , can be obtained from the Simscape logging variable, simlog, for each representation. Overlaying the simulation results from the representations permits direct comparison.
, can be obtained from the Simscape logging variable, simlog, for each representation. Overlaying the simulation results from the representations permits direct comparison.