Linearize Event-Based Subsystems (Externally Scheduled Subsystems)
Linearizing Event-Based Subsystems
Event-based subsystems (triggered subsystems) and other event-based models require special handling during linearization.
Executing a triggered subsystem depends on previous signal events, such as zero crossings. However, because linearization occurs at a specific moment in time, the trigger event never happens.
An example of an event-based subsystem is an internal combustion (IC) engine. When an engine piston approaches the top of a compression stroke, a spark causes combustion. The timing of the spark for combustion is dependent on the speed and the position of the engine crankshaft.
In the scdspeed model, triggered subsystems generate events when the
pistons reach both the top and bottom of the compression stroke. Linearization in the
presence of such triggered subsystems is not meaningful.
Approaches for Linearizing Event-Based Subsystems
You can obtain a meaningful linearization of triggered subsystems, while still preserving the simulation behavior, by recasting the event-based dynamics as one of the following:
Lumped average model that approximates the event-based behavior over time.
Periodic function call subsystem, with Normal simulation mode.
In the case of periodic function call subsystems, the subsystem linearizes to the sampling at which the subsystem is periodically executed.
In many control applications, the controller is implemented as a discrete controller, but the execution of the controller is driven by an external scheduler. You can use such linearized plant models when the controller subsystem is a periodic Function-Call Subsystem.
If recasting event-based dynamics does not produce good linearization results, try frequency response estimation. See Estimate Frequency Response Using Model Linearizer.
Note
If a triggered subsystem is disabled at the current operating condition and has at least one direct passthrough I/O pair, then the subsystem will break the linearization path during linearization. In such a case, specify a block substitution or ensure that the subsystem does not have a passthrough I/O pair.
Approximate Event-Based Subsystems Using Curve Fitting (Lump-Average Model)
This example shows how to use curve fitting to approximate event-based dynamics of an engine.
The scdspeed model linearizes to zero because the
scdspeed/Throttle & Manifold/Intake Manifold is an event-triggered
subsystem.

You can approximate the event-based dynamics of the scdspeed/Throttle &
Manifold/Intake Manifold subsystem by adding the Convert to mass
charge block inside the subsystem.

The Convert to mass charge block approximates the relationship between Air Charge, Manifold Pressure, and Engine Speed as a quadratic polynomial.
If measured data for internal signals is not available, use simulation data from the original model to compute the unknown parameters p1, p2, p3, p4, and p5 using a least squares fitting technique.
When you have measured data for internal signals, you can use the Simulink® Design Optimization™ software to compute the unknown parameters. See Engine Speed Model Parameter Estimation (Simulink Design Optimization) to learn more about computing model parameters, linearizing this approximated model, and designing a feedback controlled for the linear model.
The next figure compares the simulations of the original event-based model and the approximated model. Each of the pulses corresponds to a step change in the engine speed. The size of the step change is between 1500 and 5500. Thus, you can use the approximated model to accurately simulate and linearize the engine between 1500 RPM and 5500 RPM.

Approximate Event-Based Dynamics Using Periodic Function Call Subsystem
This example shows how to use periodic function call subsystems to approximate event-based dynamics for linearization.
Open the Simulink® model.
mdl = 'scdPeriodicFcnCall';
open_system(mdl)
Linearize the model at the model operating point.
io = getlinio(mdl); linsys = linearize(mdl,io)
linsys =
D =
Desired Wat
Water-Tank S 0
Static gain.
Model Properties
The linearization is zero because the subsystem is not a periodic function call.
Open the Externally Scheduled Controller block, which is a Function-Call Subsystem block.

Open the function block and configure it.
Set the Sample time type parameter to
periodic.Set the Sample time parameter to
0.01, which is the sample time of the controller.

Alternatively, you can configure the function block programmatically using the following code.
block = 'scdPeriodicFcnCall/Externally Scheduled Controller/function'; set_param(block,'SampleTimeType','periodic') set_param(block,'SampleTime','0.01')
Linearize the model.
linsys2 = linearize(mdl,io); bode(linsys2)
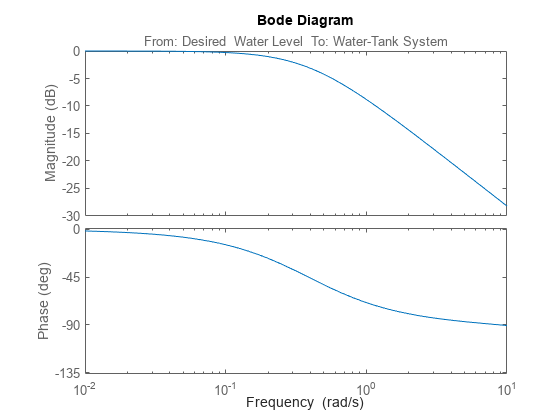
The linearization is no longer zero.