eyeContour

Contour of eye opening from eye diagram

Since R2024a

Description

Use the eye contour object to store data related to a set of contours at the specified symbol error rate (SER). The eye contours are generated from an eye diagram.

Creation

Syntax

c = eyeContour(eyeObj)

c = eyeContour(eyeObj,Name=Value)

Description

c = eyeContour(eyeObj) creates an eye contour object from the eye diagram object eyeObj using default values.

c = eyeContour(eyeObj,Name=Value) sets the Properties (Mixed-Signal Blockset) of the eye contour object to the specified values.

For example, c = eyeContour(eyeObj,SER=1e-3,Extrapolation='None') creates an eye contour object from the eye diagram object eyeObj at the symbol error rate 1e-3.

Input Arguments

eyeObj — Eye diagram object

eye diagram object

Eye diagram object used to create the eye contour object. The eye diagram object is created as an accumulation of 2-D histograms from the eye diagram data.

Properties

Contour — Numeric contour data for each eye opening

[] (default) | 3-D array

Numeric contour data consisting of upper and lower contours for each eye opening, specified as a 3-D array. Contours are row vectors with one element for each of the TimeBins properties from the original eyeDiagramSI object. The object indexes the contours from the lowest eye center amplitude to the highest.

By default, the property is automatically set from the value defined in the eyeObj eye diagram object.

Example

Contour(1, :, 3) represents the lower contour of the third eye.

Contour(2, :, 1) represents the upper contour of the first eye.

Data Types: double

OuterContour — Numeric contour data of outer contours

[] (default) | vector

Numeric contour data consisting of two outer (below and above) contours for the whole eye diagram, specified as a vector.

OuterContour(1, :) represents the lower limit of the eye. Contour(2, :) represents the upper limit of the eye.

By default, the property is automatically set from the value defined in the eyeObj eye diagram object.

Data Types: double

SER — Symbol error rate to generate contour

0 | scalar

Symbol error rate to generate contours, specified as a scalar.

Data Types: double

Extrapolation — Extrapolation method to generate contour

none (default) | dualdirac | gaussian | linear | spline | pchip | makima

Extrapolation method to generate contours. For more information, see Extrapolation (Mixed-Signal Blockset).

Data Types: char

SampleInterval — Time between adjacent samples in input data

1 (default) | scalar

Elapsed time between adjacent samples in the input data, specified as a scalar in seconds.

By default, the property is automatically set from the value defined in the eyeObj eye diagram object.

Data Types: double

SymbolTime — Time span of one symbol

8 (default) | scalar

Time span of one symbol, specified as a scalar in seconds.

By default, the property is automatically set from the value defined in the eyeObj eye diagram object.

Data Types: double

SymbolThresholds — Nominal center amplitude for eye opening

vector

Nominal center amplitude for each eye opening in the eye diagram, specified as a vector.

By default, the property is automatically set from the value defined in the eyeObj eye diagram object.

Data Types: double

Object Functions

eyeHeight (Mixed-Signal Blockset)	Measure vertical eye opening
eyeWidth (Mixed-Signal Blockset)	Measure horizontal eye opening
eyeArea (Mixed-Signal Blockset)	Measure eye area
upperContour (Mixed-Signal Blockset)	Measure upper contour of eye diagram
lowerContour (Mixed-Signal Blockset)	Measure lower contour of eye diagram
closedContour (Mixed-Signal Blockset)	Measure closed contour of eye diagram

More About

Extrapolation

The Eye Measurement block extrapolates its 2-D histogram to a specified symbol error rate whenever it generates bathtub curves or eye contours.

During extrapolation method, the block pre-processes the data, one symbol at a time on only a 1-D slice of the said symbol. The block extrapolates the eye diagram at the specified SER value using the interpolation between the adjacent bins.

The block provides five interpolation methods (none, linear, spline, pchip, and makima) and two extrapolation methods (gaussian and dualdirac) to extrapolate data.

This image shows how the block uses interpolation methods to extrapolate data.

The blue dots represent the cumulative sum of the eye diagram going outward from the center of the eye. The blue dot at the x-axis value zero represents the eye opening. The dotted red line shows the interpolated samples.

The log scale image is used to create the bathtub curves. The discontinuity at the logarithmic scale is to show the zero x-axis value. The linear scale image shows how the cumulative sum of the 1-D slice of the eye looks on the same scale as the slice itself..

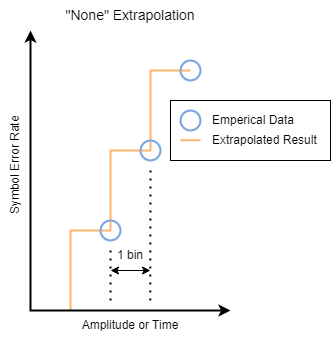
For example, the none extrapolation method uses a previous neighbor interpolation of the cumulative sum an eye slice. For horizontal eye slices, the extrapolation uses the timing origins. For vertical eye slices, the extrapolation uses the symbol thresholds.

When moving outward from the center of the eye, it is a previous neighbor interpolation. When moving across the eye from one side to the other, it appears as a next neighbor interpolation that switches to a previous neighbor interpolation as you pass the center of the eye. This way, the result for a symbol error rate is a conservative estimate from the perspective of the eye opening, based on the data.

On the other hand, the dualdirac extrapolation algorithm first fits the Dual-Dirac PDF to a column of the split histogram. Then it uses those coefficients to calculate the inverse Dual-Dirac CDF for the specified SER(s). It is only applicable to systems with an exponential impulse response whose time constant is on the order of the time for one symbol, or less. The algorithm is also significantly slower that the None extrapolation method.

This table summarizes the different extrapolation methods the block supports.

Method	Description	Comments
none	Uses previous neighbor interpolation of each eye slice to find the SER values. The interpolated value at any query point is the value at the previous sample grid point.	Fast computation time. Accurate to the data, but more susceptible to noise in individual slices.
dualdirac	Fits a Dual-Dirac model to each slice of the eye, then uses the fitted model to find the SER values.	Slower than other methods due to curve fitting. Less susceptible to noise, but less accurate to data.
gaussian	Uses the Gaussian defined by the sample mean and sample standard deviation of each eye slice to find the SER values.	Faster alternative to dualdirac. Best for automated optimization. Less susceptible to noise, but less accurate to data.
linear	Uses linear interpolation of each eye slice to find the SER values. The interpolated value at any query point is based on linear interpolation of the values at neighboring grid points in each respective dimension.	Accurate to the data, but more susceptible to noise in individual slices.
spline	Uses natural spline interpolation of the cumulative sum out from the center of each eye slice to find SER values.	Uses natural boundary conditions: the second derivative is zero at the end points. Accurate to the data, but more susceptible to noise in individual slices. Slowest of the interpolation methods, but faster than dualdirac.
pchip	Uses shape-preserving piecewise cubic interpolation of each eye slice to find the SER values. The interpolated value at any query point is based on a shape-preserving piecewise cubic interpolation of the values at neighboring grid points.	Requires more computation time than linear. Accurate to the data, but more susceptible to noise in individual slices.
makima	Uses modified Akima cubic Hermite interpolation of each eye slice to find the SER values. The interpolated value at a query point is based on any piecewise function of polynomials with degree at most three. The Akima formula is modified to avoid overshoots.	Produces fewer undulations than spline, but does not flatten as aggressively as pchip. Computation is more expensive than pchip, but typically less than spline. Accurate to the data, but more susceptible to noise in individual slices.

Version History

Introduced in R2024a