Differential
Gear mechanism that allows driven shafts to spin at different speeds
Libraries:
Simscape /
Driveline /
Gears
Description
The Differential block represents a gear mechanism that allows the driven shafts to spin at different speeds. Differentials are common in automobiles, where they enable the various wheels to spin at different speeds while cornering. Ports D, S1, and S2 represent the longitudinal driveshaft and the sun gear shafts of the differential, respectively. Any one of the shafts can drive the other two.
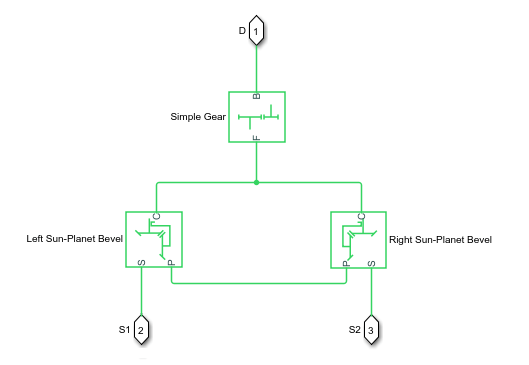
The block models the differential mechanism as a structural component based on the Simple Gear and Sun-Planet Bevel Simscape™ Driveline™ blocks. The figure demonstrates the equivalent block diagram for the Differential block.
To increase the fidelity of the gear model, specify properties such as gear inertia, meshing losses, and viscous losses. By default, gear inertia and viscous losses are assumed to be negligible. The block enables you to specify the inertias of the gear carrier and internal planet gears. To model the inertias of the outer gears, connect Simscape Inertia blocks to ports D, S1, and S2.
Thermal Modeling
You can model
the effects of heat flow and temperature change by enabling the optional thermal port. To enable
the port, set Friction model to Temperature-dependent
efficiency.
Equations
The differential imposes one kinematic constraint on the three connected axes, such that
where:
ωS1 is the velocity of sun gear shaft 1.
ωS2 is the velocity of sun gear shaft 2.
Negative values imply that the differential is left of centerline. The three degrees of freedom reduce to two independent degrees of freedom. The gear pairs are (1,2) = (S, S) and (C, D). C is the carrier.
The sum of the lateral motions is the transformed longitudinal motion. The difference of side motions, , is independent of the longitudinal motion. The general motion of the lateral shafts is a superposition of these two independent degrees of freedom, which have this physical significance:
The longitudinal degree of freedom is equivalent to the two lateral shafts rotating at the same angular velocity, , and at a fixed ratio with respect to the longitudinal shaft.
The differential degree of freedom is equivalent to keeping the longitudinal driving shaft locked, , where ωD is the velocity of the driving shaft, while the lateral shafts rotate with respect to each other in opposite directions, .
The lateral axis torques are constrained by the longitudinal axis torque such that the net power flow sums to zero:
where:
τS1 and τS2 are the torques along the lateral axes.
τD is the longitudinal torque.
Ploss is the power loss.
When the kinematic and power constraints are combined, the ideal case yields
where gD is the gear ratio for the longitudinal driveshaft.
The effective Differential block constraint is composed of two sun-planet bevel gear subconstraints.
The first subconstraint is due to the coupling of the two sun-planet bevel gears to the carrier:
where gSP1 and gSP2 are the gear ratios for the sun-planet gears.
The second subconstraint is due to the coupling of the carrier to the longitudinal driveshaft:
The sun-planet gear ratios of the underlying sun-planet bevel gears, in terms of the radii, r, of the sun-planet gears are:
The Differential block is implemented with , leaving gD free to adjust.
In the nonideal case, τloss ≠ 0. For more information, see Model Gears with Losses.
Assumptions and Limitations
The gears are assumed to be rigid.
Coulomb friction slows down simulation. For more information, see Adjust Model Fidelity.