Compute Joint Torques to Balance an Endpoint Force and Moment

Generate torques to balance an endpoint force acting on the end effector of a planar robot. The end effector can be defined at body frame of the end-effector or defined as the tool-tip frame which affixed to a point at some fixed distance from the end effector frame. To calculate the joint torques using various methods, use the geometricJacobian and inverseDynamics object functions for a rigidBodyTree robot model.

Initialize Robot

The twoJointRigidBodyTree robot is a 2-D planar robot. Joint configurations are output as column vectors.

twoJointRobot = twoJointRigidBodyTree("column");

In this example, we will emulate an external force acting on the body frame of the "tool" body. This force can also act on an arbitrary frame at a fixed distance from the "tool" body. Let that frame be called "toolTip". Add a new "toolTip" frame to the "tool" body at "[0.1,0,0]" translation vector from the "tool" body frame.

toolBody = twoJointRobot.Bodies{end};
addFrame(toolBody,"toolTip","tool",trvec2tform([0.1,0,0]));

Specify the end-effector as the "toolTip" frame. One can also toggle the end-effector to "tool" body frame by selecting it from the drop-down. The subsequent computations will still be consistent regardless of the frame.

eeFrameName = "toolTip"

eeFrameName = 
"toolTip"

Problem Setup

The endpoint force eeForce is a column vector with a combination of the linear force and moment acting on the end-effector body (at either the "tool" or "toolTip" frame). Note that this vector is expressed in the base coordinate frame and is shown below.

fx = 2; 
fy = 2;
fz = 0;
nx = 0;
ny = 0;
nz = 3;
eeForce = [nx;ny;nz;fx;fy;fz];

Specify the joint configuration of the robot for the balancing torques.

q = [pi/3;pi/4];
Tee = getTransform(twoJointRobot,q,eeFrameName);

Geometric Jacobian Method

Using the principle of virtual work [1], find the balancing torque using the geometricJacobian object function and multiplying the transpose of the Jacobian by the endpoint force vector.

J = geometricJacobian(twoJointRobot,q,eeFrameName);
jointTorques = J' * eeForce;
fprintf("Joint torques using geometric Jacobian (Nm): [%.3g, %.3g]",jointTorques);

Joint torques using geometric Jacobian (Nm): [1.16, 1.53]

Inverse Dynamics for Spatially-Transformed Force

Using another method, calculate the balancing torque by computing the inverse dynamics with the endpoint force spatially transformed to the base frame.

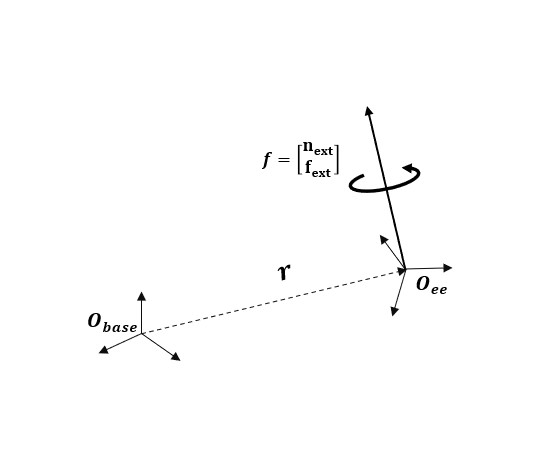
Spatially transforming a wrench from the end-effector frame to the base frame means to exert a new wrench in a frame that happens to collocate with the base frame in space, but is still fixed to the end-effector body; this new wrench has the same effect as the original wrench exerted at the end-effector origin. In the figure below, ${\mathbf{f}}_{\mathbf{ext}}$ and ${\mathbf{n}}_{\mathbf{ext}}$ are the endpoint linear force and moment respectively, and the ${\mathbf{f}}_{\mathrm{ee}}^{\mathbf{base}}$and ${\mathbf{n}}_{\mathrm{ee}}^{\mathbf{base}}$are the spatially transformed forces and moments at the end-effector (either the "tool" or "toolTip" frame) respectively. In the snippet below, fbase_ee is the spatially transformed wrench.

r = tform2trvec(Tee);
fbase_ee = [cross(r,[fx fy fz])' + [nx;ny;nz]; fx;fy;fz];
fext = -externalForce(twoJointRobot, eeFrameName, fbase_ee);
jointTorques2 = inverseDynamics(twoJointRobot, q, [], [], fext);
fprintf("Joint torques using inverse dynamics (Nm): [%.3g, %.3g]",jointTorques2)

Joint torques using inverse dynamics (Nm): [1.16, 1.53]

Inverse Dynamics for End-Effector Force

Instead of spatially transforming the endpoint force to the base frame, use a third method by expressing the end-effector force in its own coordinate frame (fee_ee). Transform the moment and the linear force vectors into the end-effector coordinate frame. Then, specify that force and the current configuration to the externalForce function. Calculate the inverse dynamics from this force vector.

eeLinearForce = Tee \ [fx;fy;fz;0];
eeMoment = Tee \ [nx;ny;nz;0];
fee_ee = [eeMoment(1:3); eeLinearForce(1:3)];
fext = -externalForce(twoJointRobot,eeFrameName,fee_ee,q);
jointTorques3 = inverseDynamics(twoJointRobot, q, [], [], fext);
fprintf("Joint torques using inverse dynamics (Nm): [%.3g, %.3g]",jointTorques3);

Joint torques using inverse dynamics (Nm): [1.16, 1.53]

References

[1]Siciliano, B., Sciavicco, L., Villani, L., & Oriolo, G. (2009). Differential kinematics and statics. Robotics: Modelling, Planning and Control, 105-160.

[2]Harry Asada, and John Leonard. 2.12 Introduction to Robotics. Fall 2005. Chapter 6 Massachusetts Institute of Technology: MIT OpenCourseWare, https://ocw.mit.edu. License: Creative Commons BY-NC-SA.