Train DDPG Agent to Swing Up and Balance Pendulum with Image Observation
This example shows how to train a deep deterministic policy gradient (DDPG) agent to swing up and balance a pendulum with an image observation modeled in MATLAB®.
For more information on DDPG agents, see Deep Deterministic Policy Gradient (DDPG) Agent.
Simple Pendulum with Image MATLAB Environment
The reinforcement learning environment for this example is a simple frictionless pendulum that initially hangs in a downward position. The training goal is to make the pendulum stand upright using minimal control effort.
For this environment:
The balanced, upright pendulum position is zero radians, and the downward hanging pendulum position is
piradians.The torque action signal from the agent to the environment is from –2 to 2 N·m (counterclockwise positive).
The observations from the environment are an image indicating the location of the pendulum mass and the pendulum angular velocity.
The reward , provided at every time step, is
Here:
is the angle of displacement from the upright position (counterclockwise positive).
is the derivative of the displacement angle.
is the control effort from the previous time step.
For more information on this model, see Load Predefined Control System Environments.
Create Environment Interface
Create a predefined environment object for the pendulum.
env = rlPredefinedEnv("SimplePendulumWithImage-Continuous")env =
SimplePendlumWithImageContinuousAction with properties:
Mass: 1
RodLength: 1
RodInertia: 0
Gravity: 9.8100
DampingRatio: 0
MaximumTorque: 2
Ts: 0.0500
State: [2×1 double]
Q: [2×2 double]
R: 1.0000e-03
The object has a continuous action space where the agent can apply a torque between –2 to 2 N·m.
Obtain the observation and action specification from the environment object.
obsInfo = getObservationInfo(env); actInfo = getActionInfo(env);
Fix the random generator seed for reproducibility.
rng(0)
Create DDPG Agent
DDPG agents use a parametrized Q-value function approximator to estimate the value of the policy. A Q-value function critic takes the current observation and an action as inputs and returns a single scalar as output (the estimated discounted cumulative long-term reward for which receives the action from the state corresponding to the current observation, and following the policy thereafter).
To model the parametrized Q-value function within the critic, use a convolutional neural network (CNN) with three input layers (one for each observation channel, as specified by obsInfo, and the other for the action channel, as specified by actInfo) and one output layer (which returns the scalar value).
Define each network path as an array of layer objects, and assign names to the input and output layers of each path, as well as to the addition and concatenation layers. These names allow you to connect the paths and then later explicitly associate the network input and output layers with the appropriate environment channel. For more information on creating representations, see Create Policies and Value Functions.
hiddenLayerSize1 = 256; hiddenLayerSize2 = 256; % Image input path imgPath = [ imageInputLayer(obsInfo(1).Dimension, ... Name="imgInLyr") convolution2dLayer(5,8,Stride=3,Padding=0) reluLayer convolution2dLayer(5,8,Stride=3,Padding=0) reluLayer fullyConnectedLayer(32) concatenationLayer(1,2,Name="cat1") fullyConnectedLayer(hiddenLayerSize1) reluLayer fullyConnectedLayer(hiddenLayerSize2) additionLayer(2,Name="add") reluLayer fullyConnectedLayer(1,Name="fc4") ]; % d(theta)/dt input path dthPath = [ featureInputLayer(prod(obsInfo(2).Dimension), ... Name="dthInLyr") fullyConnectedLayer(1,Name="fc5", ... BiasLearnRateFactor=0, ... Bias=0) ]; % Action path actPath =[ featureInputLayer(prod(obsInfo(2).Dimension), ... Name="actInLyr") fullyConnectedLayer(hiddenLayerSize2, ... Name="fc6", ... BiasLearnRateFactor=0, ... Bias=zeros(hiddenLayerSize2,1)) ];
Assemble dlnetwork object.
criticNetwork = dlnetwork(); criticNetwork = addLayers(criticNetwork,imgPath); criticNetwork = addLayers(criticNetwork,dthPath); criticNetwork = addLayers(criticNetwork,actPath); criticNetwork = connectLayers(criticNetwork,"fc5","cat1/in2"); criticNetwork = connectLayers(criticNetwork,"fc6","add/in2");
View the critic network configuration and display the number of parameters.
plot(criticNetwork)

Initialize the network and display the number of parameters.
criticNetwork = initialize(criticNetwork); summary(criticNetwork)
Initialized: true
Number of learnables: 81.2k
Inputs:
1 'imgInLyr' 50×50×1 images
2 'dthInLyr' 1 features
3 'actInLyr' 1 features
Create the critic using the specified neural network and the environment action and observation specifications. Pass as additional arguments also the names of the network layers to be connected with the observation and action channels. For more information, see rlQValueFunction.
critic = rlQValueFunction(criticNetwork, ... obsInfo,actInfo,... ObservationInputNames=["imgInLyr","dthInLyr"], ... ActionInputNames="actInLyr");
DDPG agents use a parametrized deterministic policy over continuous action spaces, which is implemented by a continuous deterministic actor. A continuous deterministic actor implements a parametrized deterministic policy for a continuous action space. This actor takes the current observation as input and returns as output an action that is a deterministic function of the observation.
To model the parametrized policy within the actor, use a neural network with two input layers (receiving the content of the two environment observation channels, as specified by obsInfo) and one output layer (which returns the action to the environment action channel, as specified by actInfo).
Define the network as an array of layer objects.
% Image input path imgPath = [ imageInputLayer(obsInfo(1).Dimension, ... Name="imgInLyr") convolution2dLayer(5,8,Stride=3,Padding=0) reluLayer convolution2dLayer(5,8,Stride=3,Padding=0) reluLayer fullyConnectedLayer(32) concatenationLayer(1,2,Name="cat1") fullyConnectedLayer(hiddenLayerSize1) reluLayer fullyConnectedLayer(hiddenLayerSize2) reluLayer fullyConnectedLayer(1) tanhLayer scalingLayer(Name="scale1", ... Scale=max(actInfo.UpperLimit)) ]; % d(theta)/dt input layer dthPath = [ featureInputLayer(prod(obsInfo(2).Dimension), ... Name="dthInLyr") fullyConnectedLayer(1, ... Name="fc5", ... BiasLearnRateFactor=0, ... Bias=0) ];
Assemble dlnetwork object.
actorNetwork = dlnetwork(); actorNetwork = addLayers(actorNetwork,imgPath); actorNetwork = addLayers(actorNetwork,dthPath); actorNetwork = connectLayers(actorNetwork,"fc5","cat1/in2");
View the actor network configuration and display the number of weights.
figure plot(actorNetwork)

Initialize the network and display the number of parameters.
actorNetwork = initialize(actorNetwork); summary(actorNetwork)
Initialized: true
Number of learnables: 80.6k
Inputs:
1 'imgInLyr' 50×50×1 images
2 'dthInLyr' 1 features
Create the actor using the specified neural network. For more information, see rlContinuousDeterministicActor.
actor = rlContinuousDeterministicActor(actorNetwork, ... obsInfo,actInfo, ... ObservationInputNames=["imgInLyr","dthInLyr"]);
Specify options for the actor and critic using rlOptimizerOptions.
criticOptions = rlOptimizerOptions( ... LearnRate=1e-03, ... GradientThreshold=1); actorOptions = rlOptimizerOptions( ... LearnRate=1e-04, ... GradientThreshold=1);
Training performance using the GPU is impacted by the batch size, network structure, and the hardware itself. Therefore, using a GPU does not always guarantee a better training performance. For more information on supported GPUs, see GPU Computing Requirements (Parallel Computing Toolbox).
Set UseGPUCritic to true to train the critic using a GPU.
UseGPUCritic = false; if canUseGPU && UseGPUCritic critic.UseDevice = "gpu"; end
Set UseGPUActor to true to train the actor using a GPU.
UseGPUActor = false; if canUseGPU && UseGPUActor actor.UseDevice = "gpu"; end
Fix the random generator seed used on the GPU for reproducibility.
if canUseGPU && (UseGPUCritic || UseGPUActor) gpurng(0) end
Specify the DDPG agent options using rlDDPGAgentOptions.
agentOptions = rlDDPGAgentOptions(... SampleTime=env.Ts,... TargetSmoothFactor=1e-3,... ExperienceBufferLength=1e6,... DiscountFactor=0.99,... MiniBatchSize=128);
You can also specify options using dot notation.
agentOptions.NoiseOptions.StandardDeviation = 0.6; agentOptions.NoiseOptions.StandardDeviationDecayRate = 1e-6; agentOptions.NoiseOptions.StandardDeviationMin = 0.1;
Specify the training options for the function approximator objects.
agentOptions.CriticOptimizerOptions = criticOptions; agentOptions.ActorOptimizerOptions = actorOptions;
Then create the agent using the specified actor, critic, and agent options. For more information, see rlDDPGAgent.
agent = rlDDPGAgent(actor,critic,agentOptions);
Train Agent
To train the agent, first specify the training options. For this example, use the following options.
Run each training for a maximum of 5000 episodes, with each episode lasting at most 400 time steps.
Display the training progress in the Reinforcement Learning Training Monitor dialog box (set the
Plotsoption).Stop training when the agent receives an evaluation statistic greater than -740. At this point, the agent can quickly balance the pendulum in the upright position using minimal control effort.
For more information on training options, see rlTrainingOptions.
maxepisodes = 5000; maxsteps = 400; trainingOptions = rlTrainingOptions(... MaxEpisodes=maxepisodes,... MaxStepsPerEpisode=maxsteps,... Plots="training-progress",... StopTrainingCriteria="EvaluationStatistic",... StopTrainingValue=-740);
Create an evaluator to evaluate the agent at every 50 training episodes.
evl = rlEvaluator(EvaluationFrequency=50, NumEpisodes=1);
You can visualize the pendulum by using the plot function during training or simulation.
plot(env)

Train the agent using the train function. Training this agent is a computationally intensive process that takes several hours to complete. To save time while running this example, load a pretrained agent by setting doTraining to false. To train the agent yourself, set doTraining to true.
doTraining = false; if doTraining % Train the agent. trainingStats = train(agent,env,trainingOptions, Evaluator=evl); else % Load pretrained agent for the example. load("SimplePendulumWithImageDDPG.mat","agent") end
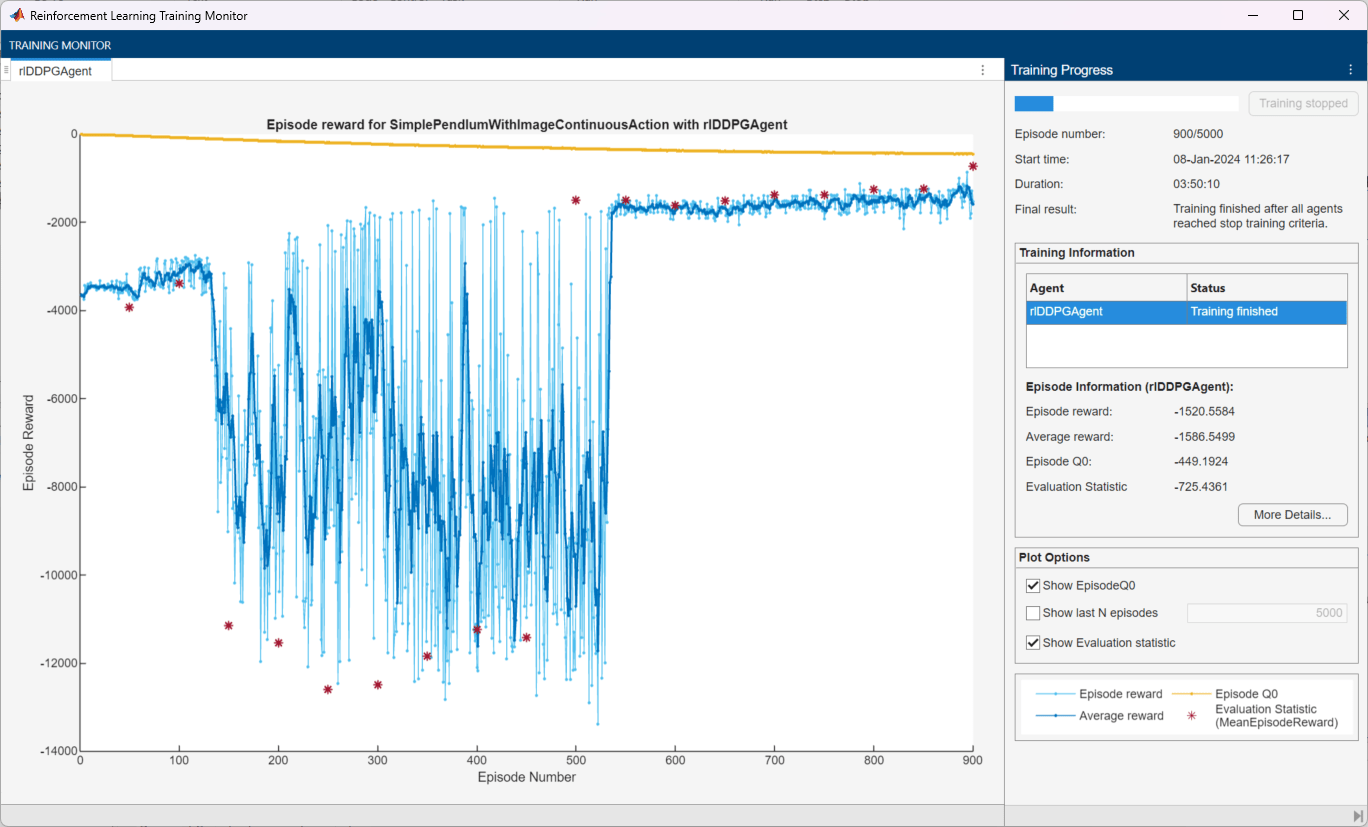
Simulate DDPG Agent
To validate the performance of the trained agent, simulate it within the pendulum environment. For more information on agent simulation, see rlSimulationOptions and sim.
rng(1); % For reproducibility
simOptions = rlSimulationOptions(MaxSteps=500);
experience = sim(env,agent,simOptions);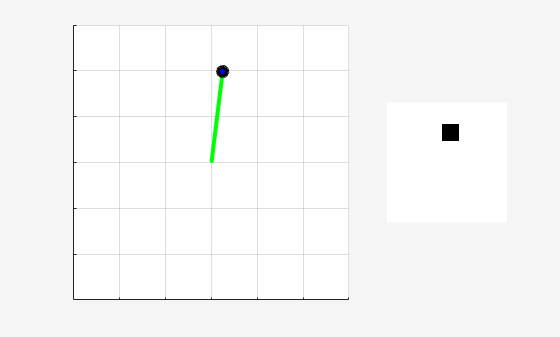
See Also
Functions
Objects
rlDDPGAgent|rlDDPGAgentOptions|rlQValueFunction|rlContinuousDeterministicActor|rlTrainingOptions|rlSimulationOptions|rlOptimizerOptions
Blocks
Topics
- Train DQN Agent to Swing Up and Balance Pendulum
- Train DDPG Agent to Swing Up and Balance Pendulum
- Train DDPG Agent to Swing Up and Balance Pendulum with Bus Signal
- Load Predefined Control System Environments
- Deep Deterministic Policy Gradient (DDPG) Agent
- Create Policies and Value Functions
- Train Reinforcement Learning Agents