Sample Matrix Inversion Beamformer
When to Use the SMI Beamformer
In situations where an airborne radar system needs to suppress clutter returns and jammer interference, the system needs a more sophisticated algorithm than a DPCA pulse canceller can provide. One option is the sample matrix inversion (SMI) algorithm. SMI is the optimum STAP algorithm and is often used as a baseline for comparison with other algorithms.
The SMI algorithm is computationally expensive and assumes a stationary environment across many pulses. If you need to suppress clutter returns and jammer interference with less computation, or in a rapidly changing environment, consider using an ADPCA pulse canceller instead.
The phased.STAPSMIBeamformer object implements
the SMI algorithm. In particular, the object lets you specify:
The number of training cells. The algorithm uses training cells to estimate the interference. In general, a larger number of training cells leads to a better estimate of interference.
The number of guard cells close to the target cells. The algorithm recognizes guard cells to prevent target returns from contaminating the estimate of the interference.
Sample Matrix Inversion Beamformer
This scenario is identical to the one presented in Adaptive DPCA Pulse Canceller To Reject Clutter and Interference. You can run the code for both examples to compare the ADPCA pulse canceller with the SMI beamformer. The example details and code are repeated for convenience.
To repeat the scenario for convenience, the airborne radar platform is a six-element ULA operating at 4 GHz. The array elements are spaced at one-half the wavelength of the 4 GHz carrier frequency. The radar emits ten rectangular pulses two μs in duration with a PRF of 5 kHz. The platform is moving along the array axis with a speed equal to one-half the product of the element spacing and the PRF. The target has a nonfluctuating RCS of 1 square meter and is moving with a constant velocity vector of (15,15,0). A stationary broadband barrage jammer is located at (3.5e3,1e3,0). The jammer has an effective radiated power of 1 kW.
PRF = 5e3; fc = 4e9; fs = 1e6; c = physconst('LightSpeed'); antenna = phased.IsotropicAntennaElement... ('FrequencyRange',[8e8 5e9],'BackBaffled',true); lambda = c/fc; array = phased.ULA(6,'Element',antenna,'ElementSpacing',lambda/2); waveform = phased.RectangularWaveform('PulseWidth', 2e-6,... 'PRF',PRF,'SampleRate',fs,'NumPulses',1); radiator = phased.Radiator('Sensor',array,... 'PropagationSpeed',c,... 'OperatingFrequency',fc); collector = phased.Collector('Sensor',array,... 'PropagationSpeed',c,... 'OperatingFrequency',fc); vy = (array.ElementSpacing * PRF)/2; transmitterplatform = phased.Platform('InitialPosition',[0;0;3e3],... 'Velocity',[0;vy;0]); % Load simulated constant gamma clutter load clutterdata target = phased.RadarTarget('MeanRCS',1,... 'Model','Nonfluctuating','OperatingFrequency',fc); targetplatform = phased.Platform('InitialPosition',[5e3; 5e3; 0],... 'Velocity',[15;15;0]); % add jammer signal with 200 samples per frame and an ERP of 1000 W. jamsig = sqrt(1000)*randn(200,1); jammerplatform = phased.Platform(... 'InitialPosition',[3.5e3; 1e3; 0],'Velocity',[0;0;0]); channel = phased.FreeSpace('OperatingFrequency',fc,... 'TwoWayPropagation',false,'SampleRate',fs); receiverpreamp = phased.ReceiverPreamp('NoiseFigure',0,... 'EnableInputPort',true,'SampleRate',fs,'Gain',40); transmitter = phased.Transmitter('PeakPower',1e4,... 'InUseOutputPort',true,'Gain',40);
Propagate the ten rectangular pulses to and from the target and collect the responses at the array. Compute clutter echoes using the constant gamma model with a gamma value corresponding to wooded terrain. Also, propagate the jamming signal from the jammer location to the airborne ULA.
NumPulses = 10; wav = waveform(); M = fs/PRF; N = array.NumElements; rxsig = zeros(M,N,NumPulses); %csig = zeros(M,N,NumPulses); jsig = zeros(M,N,NumPulses); fasttime = unigrid(0,1/fs,1/PRF,'[)'); rangebins = (c*fasttime)/2; clutter.SeedSource = 'Property'; clutter.Seed = 40543; jammer.SeedSource = 'Property'; jammer.Seed = 96703; receiverpreamp.SeedSource = 'Property'; receiverpreamp.Seed = 56113; jamloc = jammerplatform.InitialPosition; for n = 1:NumPulses [txloc,txvel] = transmitterplatform(1/PRF); % move transmitter [tgtloc,tgtvel] = targetplatform(1/PRF); % move target [~,tgtang] = rangeangle(tgtloc,txloc); % get angle to target [txsig,txstatus] = transmitter(wav); % transmit pulse %csig(:,:,n) = clutter(txsig(abs(txsig)>0)); % collect clutter txsig = radiator(txsig,tgtang); % radiate pulse txsig = channel(txsig,txloc,tgtloc,... txvel,tgtvel); % propagate pulse to target txsig = target(txsig); % reflect off target txsig = channel(txsig,tgtloc,txloc,... tgtvel,txvel); % propagate to array rxsig(:,:,n) = collector(txsig,tgtang); % collect pulse %jamsig = jammer(); % generate jammer signal [~,jamang] = rangeangle(jamloc,txloc); % angle from jammer to transmitter jamsig = channel(jamsig,jamloc,txloc,... [0;0;0],txvel); % propagate jammer signal jsig(:,:,n) = collector(jamsig,jamang); % collect jammer signal rxsig(:,:,n) = receiverpreamp(... rxsig(:,:,n) + csig(:,:,n) + jsig(:,:,n),... ~txstatus); % receive pulse plus clutter return plus jammer signal end
Determine the target's range, range gate, and two-way Doppler shift.
sp = radialspeed(tgtloc, targetplatform.Velocity, ... txloc, transmitterplatform.Velocity); tgtdoppler = 2*speed2dop(sp,lambda); tgtLocation = global2localcoord(tgtloc,'rs',txloc); tgtazang = tgtLocation(1); tgtelang = tgtLocation(2); tgtrng = tgtLocation(3); tgtcell = val2ind(tgtrng,c/(2 * fs));
Construct an SMI beamformer object. Use 100 training cells, 50 on each side of the target range gate. Use four guard cells, two range gates in front of the target cell and two range gates beyond the target cell. Obtain the beamformer response and weights.
tgtang = [tgtazang; tgtelang]; beamformer = phased.STAPSMIBeamformer('SensorArray',array,... 'PRF',PRF,'PropagationSpeed',c,... 'OperatingFrequency',fc,... 'Direction',tgtang,'Doppler',tgtdoppler,... 'WeightsOutputPort',true,... 'NumGuardCells',4,'NumTrainingCells',100); [y,weights] = beamformer(rxsig,tgtcell);
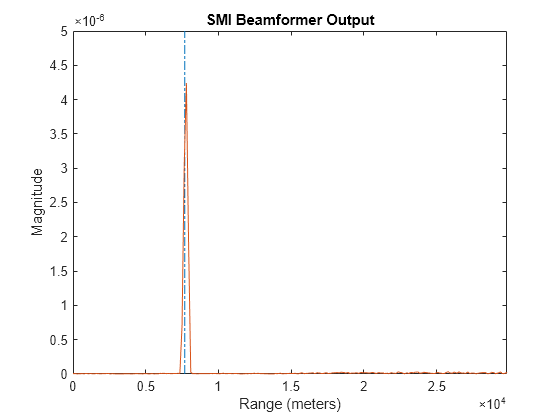
Plot the resulting array output after beamforming.
plot([tgtrng,tgtrng],[0 5e-6],'-.',rangebins,abs(y)) axis tight title('SMI Beamformer Output') xlabel('Range (meters)') ylabel('Magnitude')
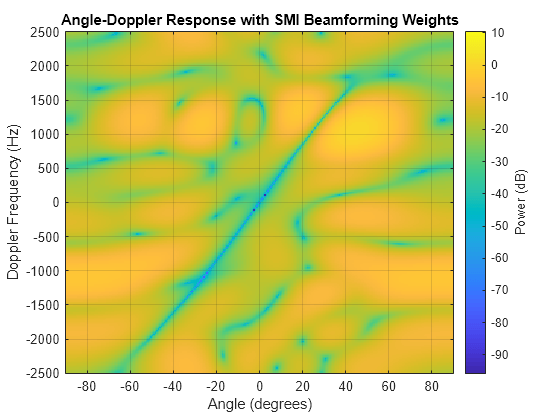
Plot the angle-Doppler response with the beamforming weights.
response = phased.AngleDopplerResponse('SensorArray',array,... 'OperatingFrequency',4e9,'PRF',PRF,... 'PropagationSpeed',physconst('LightSpeed')); plotResponse(response,weights) title('Angle-Doppler Response with SMI Beamforming Weights')