Improve Performance of Small Matrix Problems on the GPU Using pagefun
This example shows how to use pagefun to improve the performance of independent operations applied to multiple matrices arranged in a multidimensional array.
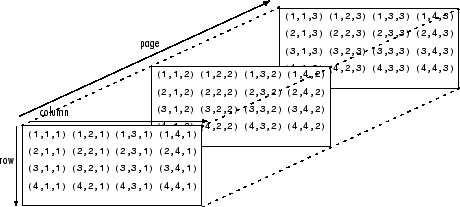
Multidimensional arrays are an extension of 2-D matrices and use additional subscripts for indexing. A 3-D array, for example uses three subscripts. The first two dimensions represent a matrix and the third represents pages of elements (sometimes referred to as slices). For more information, see Multidimensional Arrays.
While GPUs can effectively apply small independent operations to large matrices, performance is suboptimal when these operations are applied in serial, for example when the operations are applied in a for-loop. In order to avoid serial processing, the arrayfun function applies a scalar operation to each element of an array in parallel on the GPU. Similarly, the pagefun function applies a function to each page of a multidimensional GPU array.
The pagefun function supports applying most element-wise functions and a number of matrix operations that support GPU array input. MATLAB® also provides a number of dedicated page-wise functions, including pagemtimes, pagemldivide, pagemrdivide, pagetranspose, pagectranspose, pageinv, pagenorm, and pagesvd. Depending on the task, these functions might simplify your code or provide better performance than using pagefun.
In this example, a robot is navigating a known map containing a large number of features that the robot can identify using its sensors. The robot locates itself in the map by measuring the relative position and orientation of those features and comparing them to the map locations. Assuming the robot is not completely lost, it can use any difference between the two to correct its position, for instance by using a Kalman Filter. This example shows an efficient way to compute the feature positions relative to the robot.
Set Up the Map
Define the dimensions of a room containing a number of features.
roomDimensions = [50 50 5];
The supporting function randomTransforms is provided at the end of this example and initializes N transforms with random values, providing a structure as output. It represents positions and orientations using 3-by-1 vectors T and 3-by-3 rotation matrices R. The N translations are packed into a 3-by-N matrix and the rotations are packed into a 3-by-3-by-N array.
Use the randomTransforms function to set up a map of 1000 features, and a start location for the robot.
numFeatures = 1000; Map = randomTransforms(numFeatures,roomDimensions); Robot = randomTransforms(1,roomDimensions);
The plotRobot function is provided as a supporting file with this example and plots a top-down view of the room, and a close up view of the robot and nearby features. The robot is represented by a blue box with wheels and the features are represented by red circles with accompanying lines representing their orientation. To use this function, open the example as a livescript.
Call the plotRobot function.
plotRobot(Robot,Map)

Define the Equations
To correctly identify the features in the map, the robot needs to transform the map to put its sensors at the origin. Then it can find map features by comparing what it sees with what it expects to see.
For a map feature we can find its position relative to the robot and orientation by transforming its global map location:
where and are the position and orientation of the robot, and and represent the map data. The equivalent MATLAB code looks like this:
Rrel(:,:,i) = Rbot' * Rmap(:,:,i) Trel(:,i) = Rbot' * (Tmap(:,i) - Tbot)
Perform Matrix Transforms on the CPU Using a for-loop
The supporting function loopingTransform is provided at the end of this example and loops over all the transforms in turn, transforming each feature to its location relative to the robot. Note the like name-value argument for zeros function which makes the function return an array of zeros of the same data type as a prototype array. For example, if the prototype array is a gpuArray, then zeros returns a gpuArray. This allows you to use the same code on the GPU in the next section.
Time the calculations using the timeit function. The timeit function times the execution of loopingTransform multiple times and returns the median of the measurements. Since timeit requires a function with no arguments, use the @() syntax to create an anonymous function of the right form.
cpuTime = timeit(@()loopingTransform(Robot,Map,numFeatures))
cpuTime = 0.0042
Perform Matrix Transforms on the GPU Using a for-loop
To run the same code on the GPU, simply pass the input data to the function as a gpuArray. A gpuArray represents an array stored in GPU memory. Many functions in MATLAB and in other toolboxes support gpuArray objects, allowing you to run your code on GPUs with minimal changes to the code. For more information, see Run MATLAB Functions on a GPU.
Ensure that your desired GPU is available and selected.
gpu = gpuDevice;
disp(gpu.Name + " GPU selected.")NVIDIA RTX A5000 GPU selected.
Create GPU arrays containing the position and orientation of the robot and the features in the map.
gMap.R = gpuArray(Map.R); gMap.T = gpuArray(Map.T); gRobot.R = gpuArray(Robot.R); gRobot.T = gpuArray(Robot.T);
Time the calculations using the gputimeit function. The gputimeit function is the equivalent of timeit for code that includes GPU computation. It makes sure all GPU operations have finished before recording the time.
gpuTime = gputimeit(@()loopingTransform(gRobot,gMap,numFeatures))
gpuTime = 0.1905
Perform Matrix Transforms on the GPU Using pagefun
The GPU version is very slow because, although all calculations were independent, they ran in series. Using pagefun we can run all the computations in parallel.
The supporting function pagefunTransform is provided at the end of this example and applies the same transforms as the loopingTransform function using pagefun instead of a for-loop. The first computation is the calculation of the rotations. This involves a matrix multiply, which translates to the function mtimes (*). Pass this to pagefun along with the two sets of rotations to be multiplied:
Rel.R = pagefun(@mtimes,Robot.R',Map.R);
Robot.R' is a 3-by-3 matrix, and Map.R is a 3-by-3-by-N array. The pagefun function matches each independent matrix from the map to the same robot rotation, and gives us the required 3-by-3-by-N output.
The translation calculation also involves a matrix multiply, but the normal rules of matrix multiplication allow this to come outside the loop without any changes:
Rel.T = Robot.R' * (Map.T - Robot.T);
Time the calculations using the gputimeit function.
gpuPagefunTime = gputimeit(@()pagefunTransform(gRobot,gMap))
gpuPagefunTime = 3.3066e-04
Compare Results
Plot the timing results.
figure labels = categorical(["CPU Execution","GPU Execution","GPU Execution with \fontname{consolas}pagefun"]); bar(labels,[cpuTime,gpuTime,gpuPagefunTime]) ylabel("Execution Time (s)") set(gca,YScale="log")

Calculate how much faster the execution using pagefun is than CPU and simple GPU execution.
fprintf("Executing the transforms on the GPU using pagefun is %3.2f times faster than on the CPU.\n", ... cpuTime/gpuPagefunTime);
Executing the transforms on the GPU using pagefun is 12.65 times faster than on the CPU.
fprintf("Executing the transforms on the GPU using pagefun is %3.2f times faster than using for-loops on the GPU.\n", ... gpuTime/gpuPagefunTime);
Executing the transforms on the GPU using pagefun is 576.17 times faster than using for-loops on the GPU.
Locate a Lost Robot Using Multiple Possible Robot Positions
If the robot is in an unknown part of the map, it can use a global search algorithm to locate itself. The algorithm tests a number of possible locations by carrying out the above computation and looking for good correspondence between the features seen by the robot's sensors and what it would expect to see at that position.
Now there are multiple possible robot positions as well as multiple features. N features and M robots requires N*M transforms. To distinguish 'robot space' from 'feature space', use the 4th dimension for rotations and the 3rd for translations. That means that the robot rotations will be 3-by-3-by-1-by-M, and the translations will be 3-by-1-by-M.
Initialize the search with ten random robot locations. A good search algorithm would use topological or other clues to seed the search more intelligently.
numRobots = 10; Robot = randomTransforms(numRobots,roomDimensions); Robot.R = reshape(Robot.R,3,3,1,[]); % Spread along the 4th dimension Robot.T = reshape(Robot.T,3,1,[]); % Spread along the 3rd dimension
A supporting function loopingTransform2 is defined at the end of this example and performs a looping transform using two nested loops, to loop over the robots as well as over the features.
Time the calculations using timeit.
cpuTime = timeit(@()loopingTransform2(Robot,Map,numFeatures,numRobots))
cpuTime = 0.0759
Create GPU arrays containing the robot rotations and translations.
gRobot.R = gpuArray(Robot.R); gRobot.T = gpuArray(Robot.T);
Time the calculations on the GPU using gputimeit.
gpuTime = gputimeit(@() loopingTransform2(gRobot,gMap,numFeatures,numRobots))
gpuTime = 2.1059
As before, the looping version runs much slower on the GPU because it is not doing calculations in parallel.
A supporting function pagefunTransform2 is provided at the end of this example and applies the same transforms as the loopingTransform2 function using two pagefun calls instead of nested for-loops. This function needs to incorporate the transpose operator as well as mtimes into a call to pagefun. The function also applies the squeeze function to the transposed robot orientations to put the spread over robots into the 3rd dimension, to match the translations. Despite this, the resulting code is considerably more compact.
The pagefun function expands dimensions appropriately so where we multiply 3-by-3-by-1-by-M matrix Rt with 3-by-3-by-N-by-1 matrix Map.R, we get a 3-by-3-by-N-by-M matrix out.
Time the calculations on the GPU using gputimeit.
gpuPagefunTime = gputimeit(@()pagefunTransform2(gRobot,gMap))
gpuPagefunTime = 0.0014
Compare Results
Plot the timing results.
labels = categorical(["CPU Execution","GPU Execution","GPU Execution with \fontname{consolas}pagefun"]); bar(labels,[cpuTime,gpuTime,gpuPagefunTime]) ylabel("Execution Time (s)") set(gca,YScale="log")

fprintf("Executing the transforms on the GPU using pagefun is %3.2f times faster than on the CPU.\n", ... cpuTime/gpuPagefunTime);
Executing the transforms on the GPU using pagefun is 55.85 times faster than on the CPU.
fprintf("Executing the transforms on the GPU using pagefun is %3.2f times faster than using nested for-loops on the GPU.\n", ... gpuTime/gpuPagefunTime);
Executing the transforms on the GPU using pagefun is 1549.19 times faster than using nested for-loops on the GPU.
Conclusion
The pagefun function supports a number of 2-D operations, as well as most of the scalar operations supported by arrayfun. Together, these functions allow you to vectorize a range of computations involving matrix algebra and array manipulation, eliminating the need for loops and making huge performance gains.
Wherever you are doing small calculations on GPU data in a loop, you should consider converting to a vectorized implementation in this way. This can also be an opportunity to make use of the GPU to improve performance where previously it gave no performance gains.
Supporting Functions
Random Transform Function
The randomTransforms function creates matrices defining N random transforms in a room of specified dimensions. Each transform comprises a random translation T and a random rotation R. The function can be used to set up a map of features in a room and the starting position and orientation of a robot.
function Tform = randomTransforms(N,roomDimensions) % Preallocate matrices. Tform.T = zeros(3,N); Tform.R = zeros(3,3,N); for i = 1:N % Create random translation. Tform.T(:,i) = rand(3,1) .* roomDimensions'; % Create random rotation by extracting an orthonormal % basis from a random 3-by-3 matrix. Tform.R(:,:,i) = orth(rand(3,3)); end end
Looping Transform Function
The loopingTransform function transforms every feature to its location relative to the robot by looping over the transforms in turn.
function Rel = loopingTransform(Robot,Map,numFeatures) % Preallocate matrices. Rel.R = zeros(size(Map.R),like=Map.R); Rel.T = zeros(size(Map.T),like=Map.T); for i = 1:numFeatures % Find orientation of map feature relative to the robot. Rel.R(:,:,i) = Robot.R' * Map.R(:,:,i); % Find position of map feature relative to the robot. Rel.T(:,i) = Robot.R' * (Map.T(:,i) - Robot.T); end end
pagefun Transform Function
The pagefunTransform function transforms every feature to its location relative to the robot by applying the transforms using the pagefun function.
function Rel = pagefunTransform(Robot,Map) % Find orientation of map feature relative to the robot. Rel.R = pagefun(@mtimes,Robot.R', Map.R); % Apply translation. Rel.T = Robot.R' * (Map.T - Robot.T); end
Nested Looping Transform Function
The loopingTransform2 function performs a looping transform using two nested loops, to loop over the robots as well as over the features. The transforms map every feature to its location relative to every robot.
function Rel = loopingTransform2(Robot,Map,numFeatures,numRobots) % Preallocate matrices. Rel.R = zeros(3,3,numFeatures,numRobots,like=Map.R); Rel.T = zeros(3,numFeatures,numRobots,like=Map.T); for i = 1:numFeatures for j = 1:numRobots % Find orientation of map feature relative to the robot. Rel.R(:,:,i,j) = Robot.R(:,:,1,j)' * Map.R(:,:,i); % Find position of map feature relative to the robot. Rel.T(:,i,j) = ... Robot.R(:,:,1,j)' * (Map.T(:,i) - Robot.T(:,1,j)); end end end
Two-call pagefun Transform Function
The pagefunTransform2 function performs transforms to map every feature to its location relative to every robot using two calls to the pagefun function.
function Rel = pagefunTransform2(Robot,Map) % Find orientation of map feature relative to the robot. Rt = pagefun(@transpose,Robot.R); Rel.R = pagefun(@mtimes,Rt,Map.R); % Find position of map feature relative to the robot. Rel.T = pagefun(@mtimes,squeeze(Rt), ... (Map.T - Robot.T)); end
See Also
pagefun | gpuArray | arrayfun | gputimeit