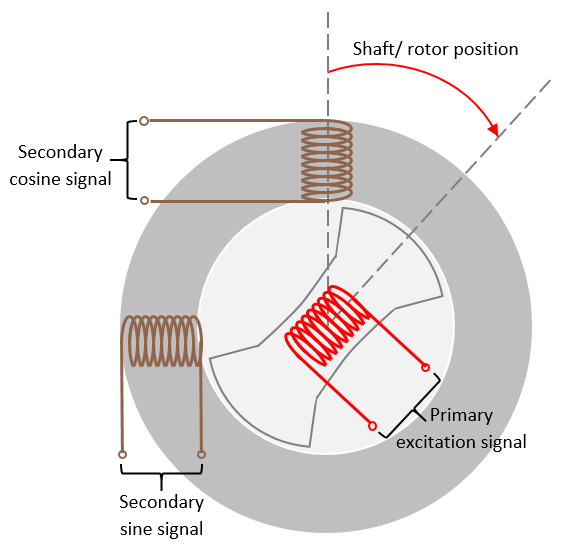
Resolver Decoder
Compute motor mechanical position and speed and sine and cosine values of motor electrical position
Libraries:
Motor Control Blockset /
Sensor Decoders
Description
The Resolver Decoder block computes the following for a resolver connected to the motor shaft:
Mechanical angular position of motor
Sine and cosine values of electrical angular position of motor
Mechanical speed of motor
A resolver uses a primary excitation input signal to generate the modulated secondary sine and cosine waveforms, which are then sampled by the ADC. The resolver utilizes one winding to two winding transformations. The sine and cosine modulation occurs in the secondary windings because of the design and construction of these windings, which places them at positions that are 90 degrees apart.

For more details about the algorithm used by the block, see .
Examples
Monitor Resolver Using Serial Communication
Use the resolver sensor to measure the rotor position. The resolver consists of two stator (secondary) windings placed orthogonally around the resolver rotor (primary) winding. After you mount the resolver sensor over a PMSM, the resolver rotor winding rotates with the shaft of the running motor. Meanwhile, the controller provides a fixed-frequency excitation signal (alternating sinusoidal or square pulse) to the primary winding.
Ports
Input
Sampled secondary sine waveform output from the resolver. When using sinusoidal excitation, normalize this signal so that it lies in the range [-1, 1] and is centred at 0.
Data Types: single | double | fixed point
Sampled secondary cosine waveform output from the resolver. When using sinusoidal excitation, normalize this signal so that it lies in the range [-1, 1] and is centred at 0.
Data Types: single | double | fixed point
Reset the phase-locked loop that the block uses internally.
Dependencies
To enable this port, set the Computation method parameter
to PLL.
Data Types: single | double | fixed point
Output
Mechanical angular position of the resolver (and the motor) in either degrees, radians, or per-unit.
Data Types: single | double | fixed point
Sine of the electrical angular position of the motor.
Data Types: single | double | fixed point
Cosine of the electrical angular position of the motor.
Data Types: single | double | fixed point
Mechanical speed of the motor in either degrees/sec, radians/sec, RPM, or per-unit.
Data Types: single | double | fixed point
This port indicates the readiness of the PLL that the block uses internally. The port can provide the following values:
1— Indicates that the PLL (and the other block outputs) are ready to use.0— Indicates that the PLL (and the other block outputs) are not yet ready.
Dependencies
To enable this port, set the Computation method parameter
to PLL.
Data Types: single | double | fixed point
Parameters
Set the Resolver Decoder block to use one of the following computation techniques:
Arithmetic— Use an algorithm based on arithmetic equations and atan2 based operations to compute the block outputs. For more information about this technique, see the section on this page.PLL— Use a PLL based algorithm to compute the block outputs. For more information about this technique, see PLL with Feed Forward.
Set the Resolver Decoder block to output one of more of the following:
Mechanical position— Enable the block to compute motor mechanical position.Sine and Cosine electrical position— Enable the block to compute sine and cosine values of motor electrical position. If you select this value, the block enables the Inputs for Sine and Cosine electrical position section in the Input Parameters tab.Mechanical speed— Enable the block to compute the mechanical speed of the motor.
Note
When you use the PLL computation technique, if you enable all the three block
outputs, then the block uses PLL to compute the sine and cosine electrical positions
and mechanical speed but uses the atan2 function to compute the
mechanical position.
Input Parameters
The number of pole pairs available in the resolver.
The resolver excitation method used to obtain the secondary sine and cosine waveforms.
When using square-pulse excitation method, the block normalizes the secondary sine and cosine inputs only if you select this parameter.
Dependencies
To enable this parameter, set Type of excitation method to
Square Pulse Excitation.
The fixed time interval (in seconds) between every two consecutive instances of block execution.
Dependencies
If you configure the block to use arithmetic computation method, you can enable this parameter by selecting the Mechanical speed parameter available in the Block Output section.
If you configure the block to use PLL computation method, the block always enables this parameter.
Inputs for Sine and Cosine electrical position
The number of pole pairs available in the motor.
Dependencies
To enable this parameter, set Block Output to
Sine and Cosine electrical position.
The offset between the resolver mechanical position and motor mechanical position (in radians).
Dependencies
To enable this parameter, set Block Output to
Sine and Cosine electrical position.
Select the rounding mode for fixed-point operations used when computing the sine and cosine of the motor electrical position.
Simplest— The block generates compact rounding code with faster computation. However, with time, this mode may add bias in the sine and cosine electrical position output.Zero— The block ensures that the rounding code does not add any bias in the sine and cosine electrical position output. However, this results in slower computation.
Dependencies
To enable this parameter, set Block Output to
Sine and Cosine electrical position.
Inputs for sinusoidal excitation method
The phase delay that the block adds to the Sin and
Cos input port signals.
Dependencies
To enable this parameter, set Type of excitation method to
Sinusoidal Excitation.
Number of samples available in one cycle of the Sin and
Cos input port signals.
Dependencies
To enable this parameter, set Type of excitation method to
Sinusoidal Excitation.
PLL Parameters
Maximum possible frequency of the input signals (in hertz).
Dependencies
To enable this parameter set the Computation method
parameter to PLL
Cutoff frequency of the lowpass filter that the block uses to filter the estimated angular frequency (in hertz).
Dependencies
To enable this parameter set the Computation method
parameter to PLL
Size of the lookup table array that the block provides to the SinCos Embedded Optimized block, which is used internally. This parameter accepts a value between 125 and 4095.
Dependencies
To enable this parameter:
Set the Computation method parameter to
PLL.Select the Mechanical position parameter available in the Block Output section.
Clear the Sine and Cosine electrical position parameter available in the Block Output section.
Proportional gain (Kp) of the PI controller used by the block to compute the angular frequency.
Dependencies
To enable this parameter set the Computation method
parameter to PLL
Integral gain (Ki) of the PI controller used by the block to compute the angular frequency.
Dependencies
To enable this parameter set the Computation method
parameter to PLL
Click Compute default parameters to calculate an approximate proportional gain (Kp) and integral gain (Ki) and update these fields.
Due to dynamics in the closed loop phase-locked loop (PLL), output of PLL takes time to reach steady state. This parameter defines a threshold that the block uses to determine if the PLL has reached steady state.
Dependencies
To enable this parameter set the Computation method
parameter to PLL
Output Parameters
The unit of the mechanical position output of the block.
Dependencies
For both arithmetic and PLL computation methods, the block enables this parameter only if you select the Mechanical position parameter available in the Block Output section.
The data type for the angular position output.
Dependencies
To enable this parameter, set the Computation method
parameter to PLL and select the Mechanical
position parameter available in the Block Output
section.
Data type of the sine-cosine lookup table used by the block.
Dependencies
To enable this parameter, set the Computation method
parameter to PLL and select the Mechanical
position parameter available in the Block Output
section.
The unit of the mechanical speed output of the block.
Dependencies
For both arithmetic and PLL computation methods, the block enables this parameter only if you select the Mechanical speed parameter available in the Block Output section.
The data type for the angular speed output.
Dependencies
To enable this parameter, set the Computation method
parameter to PLL and select the Mechanical
speed parameter available in the Block Output
section.
The rated speed of the motor (in RPM).
Dependencies
For both arithmetic and PLL computation methods, the block enables this
parameter only if you select the Mechanical speed parameter
available in the Block Output section and then set
Speed unit to Per-Unit.
Algorithms
The block uses the correctly sampled and normalized version of the secondary sine and cosine waveforms to demodulate the sine and cosine signals using which it determines the electrical position of the resolver. It converts this position into its mechanical equivalent according to the number of pole pairs available in the resolver. The resulting value indicates the mechanical position of the motor.
The block also uses the demodulated sine and cosine signals (sine and cosine of resolver electrical angle) to compute the motor speed as well as the sine and cosine values of the motor electrical position.
The block supports these excitation methods:
Sinusoidal excitation — The primary excitation signal in this method is sinusoidal. This method generates sinusoidal secondary waveforms after modulation.
Square-pulse excitation — The primary excitation signal in this method is a square pulse. This method generates square-pulse secondary signals after modulation.
When you use the sinusoidal excitation method, the block expects secondary sine and cosine resolver signals sampled, by default, at the rate of 16 samples per excitation signal cycle, as shown in the diagram. The block can also add a phase delay to the sampled sine and cosine signals with respect to the excitation signal.
When using sinusoidal excitation, the block does not normalize the modulated sine and cosine resolver output automatically. You need to normalize these modulated waveforms (within the range of [-1,1] and centred at 0) before inputting them to the block.

The block then demodulates the sampled signal. It computes the average and peak amplitude values and the sign of the peak amplitude of a signal cycle as
and
where:
is the average amplitude value of a signal cycle.
is the number of samples per excitation cycle.
is the peak amplitude value of a signal cycle.
The block computes the electrical angular position of the resolver as
where:
is the of the secondary sine signal.
is the of the secondary cosine signal.
is the electrical angular position of the resolver.
This enables the block to demodulate and extract the sine and cosine envelopes. The block uses these demodulated envelop signals to compute the block outputs.
When using the square pulse excitation method, the block expects the secondary sine and cosine signals sampled at the rate of one sample every pulse as shown below.
If you select the Enable input normalization parameter, then after receiving the discrete-time sampled waveform, the block automatically normalizes the waveform (within the range of [-1,1] and centred at 0). To perform normalization within the block, ensure that both input signals have equal peak magnitudes.

The block then demodulates the sine and cosine signals and uses the demodulated signals to compute the block outputs.
When using either sinusoidal or square-pulse excitation, the block uses the demodulated waveforms to compute the electrical position of the resolver. This resolver position can vary using either a positive ramp (for clockwise rotation) or a negative ramp (for counterclockwise rotation).
To correctly detect the wrap-around (from 0 PU to 1 PU or from 1 PU to 0 PU), the block measures the difference between the two consecutive samples. Because the input signal frequency is always less than half of the sampling frequency, a difference less than –0.5 PU indicates a positive ramp whereas a difference that is less than +0.5 PU indicates a negative ramp.
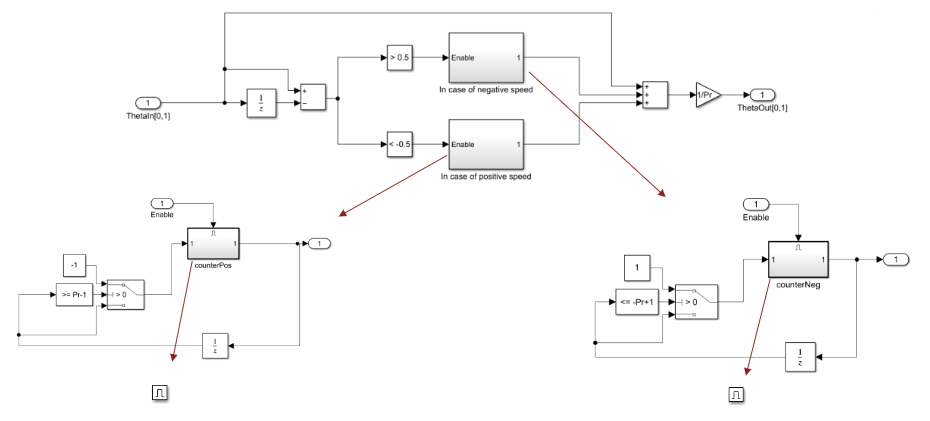
After identifying the resolver electrical position direction, the block uses the number of resolver pole pairs to compute the mechanical position of the resolver (and the motor) by extrapolating the ramp signal.
For example, for a three-pole pair resolver, the block extrapolates the ramp to achieve a magnitude that is three times the original magnitude. It then divides the value by 3 to obtain the resolver mechanical position as shown in these plots.


This section shows how the block uses arithmetic operations to compute mechanical position of the motor. Alternatively, the block can also compute the mechanical position using an algorithm based on phase-locked loop (PLL). For details about the PLL-based computation method, see PLL with Feed Forward.
When using either sinusoidal or square-pulse excitation, the block generates the demodulated sine and cosine waveforms (sine and cosine of resolver electrical position). From these demodulated waveforms, the block computes the sine and cosine of the motor electrical position using an arithmetic computation according to the ratio of the motor and resolver pole pairs. To accommodate for different possible ratios, the block utilizes unit blocks, which in turn use a structure based on the generic binary coded decimal (BCD).
For example, if the ratio of motor and resolver pole pairs (n) is 5, the following image shows the BCD-based algorithm that eventually generates the sine and cosine of the motor electrical position.
Therefore, n = number of motor pole pairs/ number of resolver pole pairs = 5.
BCD code for n = 5 is [0 0 1 0
1] or [24 23
22 21
20]. The block configures the algorithm for this
sequence as shown below.

The block supports values of n (integers) ranging from 1 to 31.
Note
The block optimizes the computation according to the ratio n. For
example, if n = 5, the block only computes
sin_2th and cos_2th twice by utilizing the
following two subsystems only.

Similarly, whenever a switch does not bypass the signals, it terminates them as shown in the diagram to ensure minimal and optimized code generation.

This section shows how the block uses arithmetic operations to compute the sine and cosine equivalents of electrical motor position. Alternatively, the block can also compute the sine and cos equivalents of electrical position using an algorithm based on phase-locked loop (PLL). For details about the PLL-based computation method, see PLL with Feed Forward.
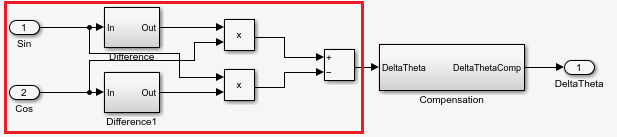
When using either sinusoidal or square-pulse excitation, the block generates the demodulated sine and cosine waveforms (sine and cosine of resolver electrical position). From these waveforms, the block computes the motor mechanical speed using the algorithm described here.
First, the block computes the difference between the two samples of these discrete time sampled signals and adds them.
In the ideal scenario, when using continuous time signals:
Where, ωr is constant with respect to time.
Because we use discrete time sampled signals:
If ωxTs is very small, then
sinωrTs approximately
equals ωrTs. This is
speed x time, therefore, this term indicates position difference for a
sample duration Δθ.
To obtain a more accurate speed, we use the Taylor series expansion of sin-1 to add the following compensation of .
Because the error is negligible, the preceding ωr value can be considered as accurate. Therefore, we can state:
where, Pr is the number of pole pairs of resolver.
The block multiplies the gain of separately to avoid data overflow when using a fixed-point data type.
Here, is the approximate compensation that the block applies to the computed speed as shown in the diagram to obtain a more accurate version of the actual mechanical speed.

where:
g is the speed conversion factor.
θ is the electrical position of the resolver.
ωr is the electrical speed of the resolver.
Δθ is the resolver electrical position difference per sample.
ω is the mechanical speed of the resolver (or motor).
Ts is the sampling time of the sine and cosine envelop signals.
Note
All block inputs should have identical amplitude and data types (either signed fixed or floating point).
This section shows how the block uses arithmetic operations to compute motor speed. Alternatively, the block can also compute the motor speed using an algorithm based on phase-locked loop (PLL). For details about the PLL-based computation method, see PLL with Feed Forward.
References
[1] The block's capability of resolver excitation using square-pulse carrier frequency is based on the collaboration (IITD/FT/03/2038/2020) between The MathWorks, Inc. and Indian Institute of Technology (IIT), Delhi - with inputs from Prof. Amit Kumar Jain (Faculty Consultant-Incharge, EE, IIT Delhi) and Apurva Verma (PhD student, IIT Delhi).
Extended Capabilities
C/C++ Code Generation
Generate C and C++ code using Simulink® Coder™.
Fixed-Point Conversion
Design and simulate fixed-point systems using Fixed-Point Designer™.
Version History
Introduced in R2020a
MATLAB Command
You clicked a link that corresponds to this MATLAB command:
Run the command by entering it in the MATLAB Command Window. Web browsers do not support MATLAB commands.
Website auswählen
Wählen Sie eine Website aus, um übersetzte Inhalte (sofern verfügbar) sowie lokale Veranstaltungen und Angebote anzuzeigen. Auf der Grundlage Ihres Standorts empfehlen wir Ihnen die folgende Auswahl: .
Sie können auch eine Website aus der folgenden Liste auswählen:
So erhalten Sie die bestmögliche Leistung auf der Website
Wählen Sie für die bestmögliche Website-Leistung die Website für China (auf Chinesisch oder Englisch). Andere landesspezifische Websites von MathWorks sind für Besuche von Ihrem Standort aus nicht optimiert.
Amerika
- América Latina (Español)
- Canada (English)
- United States (English)
Europa
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)