The Three Main Families of Map Projections
Unwrapping the Sphere to a Plane
Mapmakers have developed hundreds of map projections, over several thousand years. Three large families of map projection, plus several smaller ones, are generally acknowledged. These are based on the types of geometric shapes that are used to transfer features from a sphere or spheroid to a plane. Map projections are based on developable surfaces, and the three traditional families consist of cylinders, cones, and planes. They are used to classify the majority of projections, including some that are not analytically (geometrically) constructed. In addition, a number of map projections are based on polyhedra. While polyhedral projections have interesting and useful properties, they are not described in this guide.
Which developable surface to use for a projection depends on what region is to be mapped, its geographical extent, and the geometric properties that areas, boundaries, and routes need to have, given the purpose of the map. The following sections describe and illustrate how the cylindrical, conic, and azimuthal families of map projections are constructed and provides some examples of projections that are based on them.
Cylindrical Projections
A cylindrical projection is produced by wrapping a cylinder around a globe representing the Earth. The map projection is the image of the globe projected onto the cylindrical surface, which is then unwrapped into a flat surface. When the cylinder aligns with the polar axis, parallels appear as horizontal lines and meridians as vertical lines. Cylindrical projections can be either equal-area, conformal, or equidistant. The following figure shows a regular cylindrical or normal aspect orientation in which the cylinder is tangent to the Earth along the Equator and the projection radiates horizontally from the axis of rotation. The projection method is diagrammed on the left, and an example is given on the right (equal-area cylindrical projection, normal/equatorial aspect).
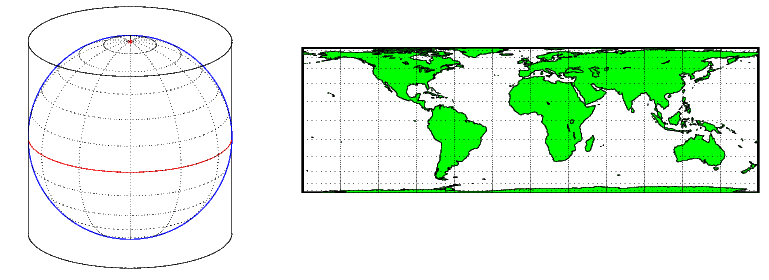
For a description of projection aspect, see Projection Aspect.
Some widely used cylindrical map projections are
Equal-area cylindrical projection
Equidistant cylindrical projection
Mercator projection
Miller projection
Plate Carrée projection
Universal transverse Mercator projection
Pseudocylindrical Map Projections
All cylindrical projections fill a rectangular plane. Pseudocylindrical projection outlines tend to be barrel-shaped rather than rectangular. However, they do resemble cylindrical projections, with straight and parallel latitude lines, and can have equally spaced meridians, but meridians are curves, not straight lines. Pseudocylindrical projections can be equal-area, but are not conformal or equidistant.
Some widely-used pseudocylindrical map projections are
Eckert projections (I-VI)
Goode homolosine projection
Mollweide projection
Quartic authalic projection
Robinson projection
Sinusoidal projection
Conic Projections
A conic projection is derived from the projection of the globe onto a cone placed over it. For the normal aspect, the apex of the cone lies on the polar axis of the Earth. If the cone touches the Earth at just one particular parallel of latitude, it is called tangent. If made smaller, the cone will intersect the Earth twice, in which case it is called secant. Conic projections often achieve less distortion at mid- and high latitudes than cylindrical projections. A further elaboration is the polyconic projection, which deploys a family of tangent or secant cones to bracket a succession of bands of parallels to yield even less scale distortion. The following figure illustrates conic projection, diagramming its construction on the left, with an example on the right (Albers equal-area projection, polar aspect).

Some widely-used conic projections are
Albers Equal-area projection
Equidistant projection
Lambert conformal projection
Polyconic projection
Azimuthal Projections
An azimuthal projection is a projection of the globe onto a plane. In polar aspect, an azimuthal projection maps to a plane tangent to the Earth at one of the poles, with meridians projected as straight lines radiating from the pole, and parallels shown as complete circles centered at the pole. Azimuthal projections (especially the orthographic) can have equatorial or oblique aspects. The projection is centered on a point, that is either on the surface, at the center of the Earth, at the antipode, some distance beyond the Earth, or at infinity. Most azimuthal projections are not suitable for displaying the entire Earth in one view, but give a sense of the globe. The following figure illustrates azimuthal projection, diagramming it on the left, with an example on the right (orthographic projection, polar aspect).

Some widely used azimuthal projections are
Equidistant azimuthal projection
Gnomonic projection
Lambert equal-area azimuthal projection
Orthographic projection
Stereographic projection
Universal polar stereographic projection