Quantify Map Distortions at Point Locations
The tissot and mdistort functions provide synoptic visual overviews of different forms of map
projection error. Sometimes, however, you need numerical estimates of error at specific
locations in order to quantify or correct for map distortions. This is useful, for example, if
you are sampling environmental data on a uniform basis across a map, and want to know
precisely how much area is associated with each sample point, a statistic that will vary by
location and be projection dependent. Once you have this information, you can adjust
environmental density and other statistics you collect for areal variations induced by the map
projection.
A Mapping Toolbox™ function returns location-specific map error statistics from the current
projection or an mstruct. The distortcalc function computes the same distortion statistics as
mdistort does, but for specified locations provided as arguments. You
provide the latitude-longitude locations one at a time or in vectors. The general form
is
[areascale,angdef,maxscale,minscale,merscale,parscale] = ...
distortcalc(mstruct,lat,long)However, if you are evaluating the current map figure, omit the
mstruct. You need not specify any return values following the last one of
interest to you.
Use distortcalc to Determine Map Projection Geometric Distortions
The following exercise uses distortcalc to compute the maximum area
distortion for a map of Argentina from the land areas data set.
Read the North and South America polygon:
Americas = shaperead('landareas.shp','UseGeoCoords',true, ... 'Selector', {@(name) ... strcmpi(name,{'north and south america'}),'Name'});Set the spatial extent (map limits) to contain the southern part of South America and also include an area closer to the South Pole:
mlatlim = [-72.0 -20.0]; mlonlim = [-75.0 -50.0]; [alat, alon] = maptriml([Americas.Lat], ... [Americas.Lon], mlatlim, mlonlim);Create a Mercator cylindrical conformal projection using these limits, specify a five-degree graticule, and then plot the outline for reference:
figure; axesm('MapProjection','mercator','grid','on', ... 'MapLatLimit',mlatlim,'MapLonLimit',mlonlim,... 'MLineLocation',5, 'PLineLocation',5) plotm(alat,alon,'b')The map looks like this:

Sample every tenth point of the patch outline for analysis:
alats = alat(1:10:numel(alat)); alons = alon(1:10:numel(alat));
Compute the area distortions (the first value returned by
distortcalc) at the sample points:adistort = distortcalc(alats, alons);
Find the range of area distortion across Argentina (percent of a unit area on, in this case, the equator):
adistortmm = [min(adistort) max(adistort)] adistortmm = 1.1790 2.7716As Argentina occupies mid southern latitudes, its area on a Mercator map is overstated, and the errors vary noticeably from north to south.
Remove any
NaNs from the coordinate arrays and plot symbols to represent the relative distortions as proportional circles, usingscatterm:nanIndex = isnan(adistort); alats(nanIndex) = []; alons(nanIndex) = []; adistort(nanIndex) = []; scatterm(alats,alons,20*adistort,'red','filled')
The resulting map is shown below:
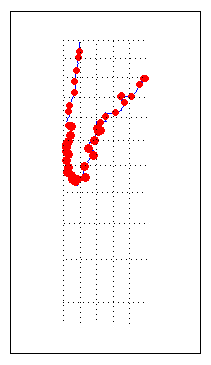
The degree of area overstatement would be considerably larger if it extended farther toward the pole. To see how much larger, get the area distortion for 50°S, 60°S, and 70°S:
a=distortcalc(-50,-60) a = 2.4203 a=distortcalc(-60,-60) a = 4 >> a=distortcalc(-70,-60) a = 8.5485Note
You can only use
distortcalcto query locations that are within the current map frame ormstructlimits. Outside points yieldNaNas a result.Using this technique, you can write a simple script that lets you query a map repeatedly to determine distortion at any desired location. You can select locations with the graphic cursor using
inputm. For example,[plat plon] = inputm(1) plat = -62.225 plon = -72.301 >> a=distortcalc(plat,plon) a = 4.6048Naturally the answer you get will vary depending on what point you pick. Using this technique, you can write a simple script that lets you query a map repeatedly to determine any distortion statistic at any desired location.
Try changing the map projection or even the orientation vector to see how the choice of
projection affects map distortion. For further information, see the reference page for
distortcalc.