Estimate Stockpile Volume from Aerial Lidar Data

This example shows how to estimate the volume of a stockpile from aerial point cloud data.

Stockpile refers to a large supply of materials, such as metals, chemicals, or other inventory, usually held in reserve at a dedicated storage facility. Stockpiles need bulk machinery, such as trucks and bulldozers, for maintenance.

Stockpile measurement techniques help in estimating the weight, volume, and size of a stockpile. Accurate stockpile measurement helps companies in the mining, construction, and shipping industries make profitable business decisions, which include:

• Efficient inventory management

• Using stockpile data for strategic planning

• Protection of personnel, material, and machinery

• Systematic downtime and maintenance

The example show how to compute the stockpile volume from an aerial point cloud using these steps.

1. Load point cloud data.

2. Extract stockpile points from the point cloud using ground segmentation and plane-fitting.

3. Transform the stockpile plane to align it with the z-axis.

4. Convert the transformed stockpile point cloud into a surface mesh, and compute the mesh volume.

Load and Visualize Data

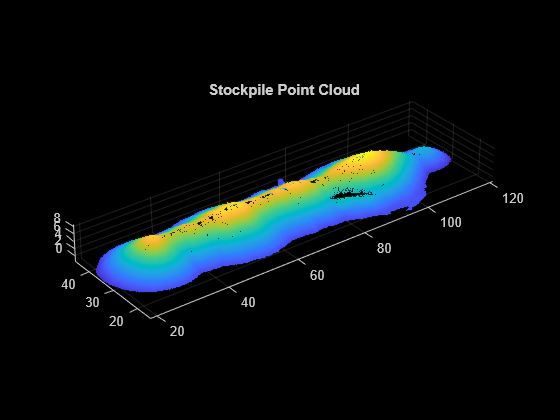
Load the point cloud data into the workspace using the pcread function and visualize the point cloud.

% Read the point cloud
ptCloud = pcread("stockpile.pcd");
% Visualize the point cloud
figure
pcshow(ptCloud)
title("Stockpile Point Cloud")

Segment Ground Plane from Point Cloud

Use these steps to segment the ground plane from the input point cloud.

1. Define a boundary around the point cloud to identify the ground plane.

2. Fit a plane to the boundary points.

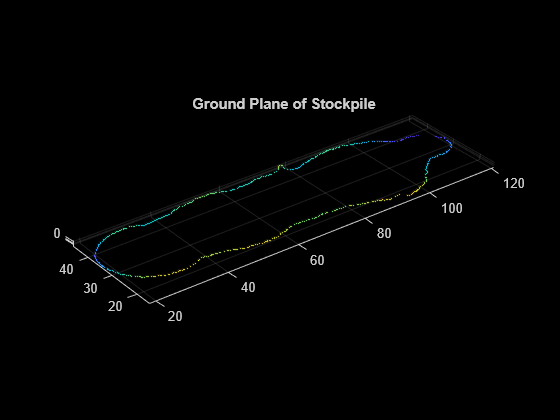
Identify the boundary points that form the outer edge of the ground surface of the stockpile.

% Define a boundary around the point cloud
boundaryIndices = boundary(double(ptCloud.Location(:,1)),double(ptCloud.Location(:,2)));
boundaryPtCloud = pointCloud([ptCloud.Location(boundaryIndices,:)]);

Fit a plane to these boundary points by using the pcfitplane function.

% Specify the maximum distance from an inlier point to the plane
maxDistance = 1.0;
% Fit a plane to the point cloud with boundary points 
[groundPlane,inlierIndices] = pcfitplane(boundaryPtCloud,maxDistance);
groundPlanePtCloud = select(boundaryPtCloud,inlierIndices);
% Visualize the ground points
figure
pcshow(groundPlanePtCloud)
title("Ground Plane of Stockpile")

Transform Point Cloud to XY-Plane

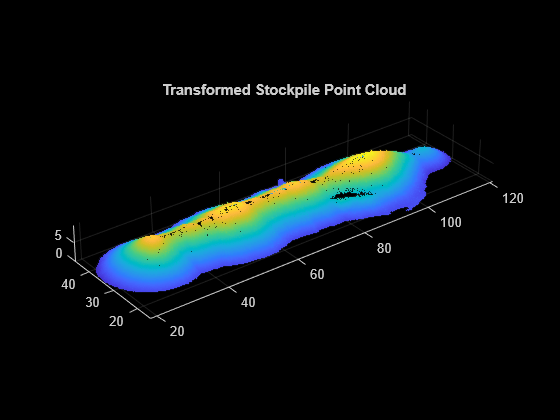
To accurately compute the volume, transform the input point cloud to align it with the xy-plane.

First, estimate the rigid transformation between the ground plane of the point cloud and the xy-plane by using the normalRotation function.

% Estimate the rigid transformation
referenceVector = [0 0 1];
tform = normalRotation(groundPlane,referenceVector);

Next, transform the point cloud to align it with the z-axis by using the pctransform function.

% Transform the point cloud
stockpilePtCloud = pctransform(ptCloud,tform);

After the transformation, some ground points of the stockpile point cloud might lie above or below the xy-plane. Apply another transformation to translate the outlier points such that all ground points have a z value of 0.

Note: You must adjust the translation parameters based on the input point cloud.

% Translation the outlier points
if abs(stockpilePtCloud.ZLimits(1)) > 0.1
    angles = [0 0 0];
    translation = [0 0 -stockpilePtCloud.ZLimits(1)];
    tform = rigidtform3d(angles,translation);
    stockpilePtCloud = pctransform(stockpilePtCloud,tform);
end
% Visualize the transformed stockpile point cloud
figure
pcshow(stockpilePtCloud)
title("Transformed Stockpile Point Cloud")

Convert Stockpile Point Cloud to Surface Mesh

Estimate connections between the surface points of the stockpile point cloud by using the Delaunay triangulation method.

% Estimate the connections between the vertices
DT = delaunayTriangulation(double(stockpilePtCloud.Location(:,1)),double(stockpilePtCloud.Location(:,2)));

Use the vertices to generate a surface mesh by using the surfaceMesh function, and visualize the generated mesh.

% Create a surface mesh around the stockpile point cloud
mesh = surfaceMesh(double(stockpilePtCloud.Location),DT.ConnectivityList);
% Visualize the surface mesh 
surfaceMeshShow(mesh)

Estimate Volume of Stockpile

Estimate the volume of the stockpile mesh.

% Estimate the volume of the stockpile mesh
volume = 0;
for i = 1:size(mesh.Faces,1)
    tri = mesh.Faces(i,:);
    x = mesh.Vertices(tri(1),:);
    y = mesh.Vertices(tri(2),:);
    z = mesh.Vertices(tri(3),:);
    partialVol = (x(3)+y(3)+z(3))*(x(1)*y(2)-y(1)*x(2)+y(1)*z(2)-z(1)*y(2)+z(1)*x(2)-x(1)*z(2))/6;
    volume = volume + partialVol;
end
disp("Estimated Volume of Stockpile = " + volume + " cubic metres")

Estimated Volume of Stockpile = 10227.4237 cubic metres

Tips

For accurate volume measurement:

1. As a preprocessing step to this workflow, remove the outliers and nonground objects from the input point cloud by using functions such as segmentGroundSMRF.

2. A high-density point cloud can improve the accuracy of volume estimation, especially for irregular or complex stockpiles.