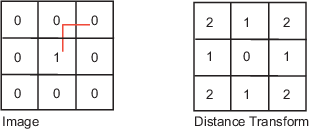
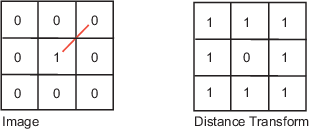
Distance Transform of a Binary Image
The distance transform provides a metric or measure of the separation of points in the
image. The bwdist function calculates the distance
between each pixel that is set to off (0) and the
nearest nonzero pixel for binary images.
The bwdist function supports several distance metrics.
Distance Metrics
Distance Metric | Description | Illustration |
|---|---|---|
Euclidean | The Euclidean distance is the straight-line distance between two pixels. |
|
City Block | The city block distance metric measures the path between the pixels based on a 4-connected neighborhood. Pixels whose edges touch are 1 unit apart; pixels diagonally touching are 2 units apart. |
|
Chessboard | The chessboard distance metric measures the path between the pixels based on an 8-connected neighborhood. Pixels whose edges or corners touch are 1 unit apart. |
|
Quasi-Euclidean | The quasi-Euclidean metric measures the total Euclidean distance along a set of horizontal, vertical, and diagonal line segments. |
|
This example creates a binary image containing two intersecting circular objects.
center1 = -10; center2 = -center1; dist = sqrt(2*(2*center1)^2); radius = dist/2 * 1.4; lims = [floor(center1-1.2*radius) ceil(center2+1.2*radius)]; [x,y] = meshgrid(lims(1):lims(2)); bw1 = sqrt((x-center1).^2 + (y-center1).^2) <= radius; bw2 = sqrt((x-center2).^2 + (y-center2).^2) <= radius; bw = bw1 | bw2; figure imshow(bw)
To compute the distance transform of the complement of the binary image, use the
bwdist function. In the image of the distance transform, note
how the centers of the two circular areas are white.
D = bwdist(~bw); figure imshow(D,[])