Pressure-Compensated Pump (IL)

Constant-pressure, variable-displacement pump in an isothermal liquid network

Since R2020a

• 

Libraries:
Simscape / Fluids / Isothermal Liquid / Pumps & Motors

Description

The Pressure-Compensated Pump (IL) block models a constant-pressure, variable-displacement pump in an isothermal liquid network. The pump displacement is controlled by the differential pressure, p_control, measured between ports X and Y. When this pressure exceeds the Set pressure differential, the fluid displacement is adjusted according to the pump Leakage and friction parameterization. The variable-displacement functionality occurs within the Pressure regulation range between the Maximum displacement, at p_set, and the Minimum displacement, at p_max.

The fluid may move from port A to port B, called forward mode, or from port B to port A, called reverse mode. Pump mode operation occurs when there is a pressure gain in the direction of the flow. Motor mode operation occurs when there is a pressure drop in the direction of the flow.

Shaft rotation corresponds to the sign of the fluid volume moving through the pump. Positive fluid displacement corresponds to positive shaft rotation in forward mode. Negative fluid displacement corresponds to negative shaft angular velocity in forward mode.

Operation Modes

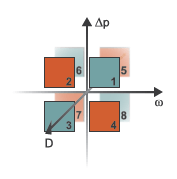
The block has eight modes of operation. The working mode depends on the pressure gain from port A to port B, Δp = p_B – p_A; the angular velocity, ω = ω_R – ω_C; and the fluid volumetric displacement, set by the pressure differential. The figure above maps these modes to the octants of a Δp-ω-D chart:

• Mode 1, Forward Pump: Positive shaft angular velocity causes a pressure increase from port A to port B and flow from port A to port B.

• Mode 2, Reverse Motor : Flow from port B to port A causes a pressure decrease from B to A and negative shaft angular velocity.

• Mode 3, Reverse Pump: Negative shaft angular velocity causes a pressure increase from port B to port A and flow from B to A.

• Mode 4, Forward Motor: Flow from port A to B causes a pressure decrease from A to B and positive shaft angular velocity.

• Mode 5, Reverse Motor : Flow from port B to port A causes a pressure decrease from B to A and positive shaft angular velocity.

• Mode 6, Forward Pump: Negative shaft angular velocity causes pressure increase from A to B and flow from A to B.

• Mode 7, Forward Motor: Flow from port A to B causes a pressure decrease from A to B and negative shaft angular velocity.

• Mode 8, Reverse Pump: Positive shaft angular velocity causes a pressure increase from port B to port A and flow from B to A.

The block has analytical, lookup table, and physical signal parameterizations. When using tabulated data or an input signal for parameterization, you can choose to characterize pump operation based on efficiency or losses.

The threshold parameters Pressure gain threshold for pump-motor transition, Angular velocity threshold for pump-motor transition, and Displacement threshold for pump-motor transition identify regions where numerically smoothed flow transition between the pump operational modes can occur. For the pressure and angular velocity thresholds, choose a transition region that provides some margin for the transition term, but which is small enough relative to the typical pump pressure gain and angular velocity so that it will not impact calculation results. For the displacement threshold, choose a threshold value that is smaller than the typical displacement volume during normal operation.

Analytical Leakage and Friction Parameterization

If you set Leakage and friction parameterization to Analytical, the block calculates leakage and friction from constant values for shaft velocity, pressure gain, and torque. The leakage flow rate, which is correlated with the pressure differential over the pump, is calculated as:

$${\dot{m}}_{leak}=K{\rho }_{avg}\Delta p,$$

where:

• Δp_nom is p_B – p_A.

• ρ_avg is the average fluid density.

• K is the Hagen-Poiseuille coefficient for analytical loss,

  $$K=\frac{D_{nom}{\omega }_{nom}\left(1-{\eta }_{v,nom}\right)}{\Delta p_{nom}},$$

  where:

  • D_nom is the Nominal displacement.

  • ω_nom is the Nominal shaft angular velocity.

  • η_nom is the Volumetric efficiency at nominal conditions.

  • Δp_nom is the Nominal pressure gain.

The friction torque, which is related to the pump pressure differential, is calculated as:

$${\tau }_{fr}=\left({\tau }_0+k\left|\Delta p\frac{D}{D_{nom}}\right|\right)\tanh \left(\frac{4\omega }{5\times {10}^{-5}{\omega }_{nom}}\right),$$

where:

• τ₀ is the No-load torque.

• k is the friction torque vs. pressure gain coefficient at nominal displacement, which is determined from the Mechanical efficiency at nominal conditions, η_m,nom:

  $$k=\frac{{\tau }_{fr,nom}-{\tau }_0}{\Delta p_{nom}}.$$

  τ_fr,nom is the friction torque at nominal conditions:

  $${\tau }_{fr,nom}=\left(\frac{1-{\eta }_{m,nom}}{{\eta }_{m,nom}}\right)D_{nom}\Delta p_{nom}.$$

• ω is the relative shaft angular velocity, or $${\omega }_R-{\omega }_C$$.

Tabulated Data Parameterizations

When using tabulated data for pump efficiencies or losses, you can provide data for one or more of the pump operational modes. The signs of the tabulated data determine the operational regime of the block. When data is provided for less than eight operational modes, the block calculates the complementing data for the other mode(s) by extending the given data into the remaining octants.

The Tabulated data - volumetric and mechanical efficiencies parameterization

The leakage flow rate is calculated as:

$${\dot{m}}_{leak}={\dot{m}}_{leak,pump}\left(\frac{1+\alpha }{2}\right)+{\dot{m}}_{leak,motor}\left(\frac{1-\alpha }{2}\right),$$

where:

• $${\dot{m}}_{leak,pump}=\left(1-{\eta }_{\upsilon }\right){\dot{m}}_{ideal}$$

• $${\dot{m}}_{leak,motor}=\left({\eta }_v-1\right)\dot{m}$$

and η_v is the volumetric efficiency, which is interpolated from the user-provided tabulated data. The transition term, α, is

$$\alpha =\tanh \left(\frac{4\Delta p}{\Delta p_{threshold}}\right)\tanh \left(\frac{4\omega }{{\omega }_{threshold}}\right)\tanh \left(\frac{4D}{D_{threshold}}\right),$$

where:

• Δp is p_B – p_A.

• p_threshold is the Pressure gain threshold for pump-motor transition.

• ω is ω_R – ω_C.

• ω_threshold is the Angular velocity threshold for pump-motor transition.

The friction torque is calculated as:

$${\tau }_{fr}={\tau }_{fr,pump}\left(\frac{1+\alpha }{2}\right)+{\tau }_{fr,motor}\left(\frac{1-\alpha }{2}\right),$$

where:

• $${\tau }_{fr,pump}=\left(1-{\eta }_m\right)\tau$$

• $${\tau }_{fr,motor}=\left({\eta }_m-1\right){\tau }_{ideal}$$

and η_m is the mechanical efficiency, which is interpolated from the user-provided tabulated data.

The Tabulated data - volumetric and mechanical losses parameterization

The leakage flow rate is calculated as:

$${\dot{m}}_{leak}={\rho }_{avg}{q}_{loss}\left(\Delta p,\omega ,D\right),$$

where q_loss is interpolated from the Volumetric loss table, q_loss(dp,w,D) parameter, which is based on user-supplied data for pressure gain, shaft angular velocity, and fluid volumetric displacement.

The shaft friction torque is calculated as:

$${\tau }_{fr}={\tau }_{loss}\left(\Delta p,\omega ,D\right),$$

where τ_loss is interpolated from the Mechanical loss table, torque_loss(dp,w,D) parameter, which is based on user-supplied data for pressure gain, shaft angular velocity, and fluid volumetric displacement.

Input Signal Parameterization

When you select Input signal - volumetric and mechanical efficiencies, ports EV and EM are enabled. The internal leakage and shaft friction are calculated in the same way as the Tabulated data - volumetric and mechanical efficiencies parameterization, except that η_v and η_m are received directly at ports EV and EM, respectively.

When you select Input signal - volumetric and mechanical losses, ports LV and LM are enabled. These ports receive leakage flow and friction torque as positive physical signals. The leakage flow rate is calculated as:

$${\dot{m}}_{leak}={\rho }_{avg}{q}_{LV}\tanh \left(\frac{4\Delta p}{p_{thresh}}\right),$$

where:

• q_LV is the leakage flow received at port LV.

• p_thresh is the Pressure gain threshold for pump-motor transition parameter.

The friction torque is calculated as:

$${\tau }_{fr}={\tau }_{LM}\tanh \left(\frac{4\omega }{{\omega }_{thresh}}\right),$$

where

• τ_LM is the friction torque received at port LM.

• ω_thresh is the Angular velocity threshold for pump-motor transition parameter.

The volumetric and mechanical efficiencies range between the user-defined specified minimum and maximum values. Any values lower or higher than this range will take on the minimum and maximum specified values, respectively.

Pump Operation

The pump flow rate is:

$$\dot{m}={\dot{m}}_{ideal}-{\dot{m}}_{leak},$$

where $${\dot{m}}_{ideal}={\rho }_{avg}D\cdot \omega .$$

The pump torque is:

$$\tau ={\tau }_{ideal}+{\tau }_{fr},$$

where $${\tau }_{ideal}=D\cdot \Delta p.$$

The mechanical power delivered by the pump shaft is:

$${\phi }_{mech}=\tau \omega ,$$

and the pump hydraulic power is:

$${\phi }_{hyd}=\frac{\Delta p\dot{m}}{{\rho }_{avg}}.$$

To be notified if the block is operating beyond the supplied tabulated data, set Check if operating beyond the range of supplied tabulated data to Warning to receive a warning if this occurs, or Error to stop the simulation when this occurs. For parameterization by input signal for volumetric or mechanical losses, you can be notified if the simulation surpasses operating modes with the Check if operating beyond pump mode parameter.

You can also monitor pump functionality. Set Check if pressures are less than pump minimum pressure to Warning to receive a warning if this occurs, or Error to stop the simulation when this occurs.

Displacement Parameterization

The linear parameterization of the pump displacement is:

$$D=\widehat{p}\left(D_{\min }-D_{\max }\right)+D_{\max },$$

where the normalized pressure, $$\widehat{p}$$, is

$$\widehat{p}=\frac{p_{control}-p_{set}}{p_{max}-p_{set}}.$$

where p_max is the sum of the Set pressure differential and the Pressure regulation range.

Displacement Dynamics

If displacement dynamics are modeled, a lag is introduced to the flow response to the modeled control pressure. p_control becomes the dynamic control pressure, p_dyn; otherwise, p_control is the steady-state pressure. The instantaneous change in dynamic control pressure is calculated based on the Time constant, τ:

$${\dot{p}}_{dyn}=\frac{p_{control}-p_{dyn}}{\tau }.$$

By default, Displacement dynamics is set to Off.

Numerically-Smoothed Pressure

You can maintain numerical robustness in your simulation by adjusting the Smoothing factor parameter. If the Smoothing factor parameter is nonzero, the block smoothly saturates the normalized control pressure between p_set and p_max. For more information, see Numerical Smoothing.

Ports

Conserving

A — Liquid port

isothermal liquid

Entry or exit port of the liquid to or from the pump.

B — Liquid port

isothermal liquid

Entry or exit port of the liquid to or from the pump.

X — Pressure reference P_x, MPa

isothermal liquid

Control pressure in units of MPa, denoted P_x. The control pressure, P_x – P_y, is compared against the Set pressure differential to trigger or moderate variable pump displacement.

Y — Pressure reference P_y, MPa

isothermal liquid

Control pressure in units of MPa, denoted P_y. The control pressure, P_x – P_y, is compared against the Set pressure differential to trigger or moderate variable pump displacement.

R — Mechanical port

mechanical rotational

Rotating shaft angular velocity and torque.

C — Mechanical port

mechanical rotational

Pump casing reference angular velocity and torque.

EV — Volumetric efficiency

physical signal

Pump efficiency for fluid displacement, specified as a physical signal. The value must be between 0 and 1.

Dependencies

To enable this port, set Leakage and friction parameterization to Input signal - volumetric and mechanical efficiencies.

EM — Mechanical efficiency

physical signal

Pump efficiency for the mechanical supply of energy, specified as a physical signal. The value must be between 0 and 1.

Dependencies

To enable this port, set Leakage and friction parameterization to Input signal - volumetric and mechanical efficiencies.

LV — Leakage flow rate, m^3/s

physical signal

Pump losses associated with fluid displacement in m³/s, specified as a physical signal.

Dependencies

To enable this port, set Leakage and friction parameterization to Input signal - volumetric and mechanical losses.

LM — Friction torque, N*m

physical signal

Pump losses associated with the mechanical supply of energy in N*m, specified as a physical signal.

Dependencies

To enable this port, set Leakage and friction parameterization to Input signal - volumetric and mechanical losses.

Parameters

Pump

Leakage and friction parameterization — Method of calculating leakage flow rate and friction torque

Analytical (default) | Tabulated data - volumetric and mechanical efficiencies | Tabulated data - volumetric and mechanical losses | Input signal - volumetric and mechanical efficiencies | Input signal - volumetric and mechanical losses

Parameterization of the leakage and friction characteristics of the pump.

• In the Analytical parameterization, the leakage flow rate and the friction torque are calculated by analytical equations.

• In the Tabulated data - volumetric and mechanical efficiencies parameterization, the volumetric and mechanical efficiencies are calculated from the user-supplied Pressure gain vector, dp, Shaft angular velocity vector, w, and Displacement vector, D parameters and interpolated from the 3-D Volumetric efficiency table, e_v(dp,w,D) and Mechanical efficiency table, e_m(dp,w,D) tables.

• In the Tabulated data - volumetric and mechanical losses parameterization, the leakage flow rate and friction torque are calculated from the user-supplied Pressure gain vector, dp, Shaft angular velocity vector, w, and Displacement vector, D parameters and interpolated from the 3-D Volumetric loss table, q_loss(dp,w,D) and Mechanical loss table, torque_loss(dp,w,D) parameters.

• In the Input signal - volumetric and mechanical efficiencies parameterization, the volumetric and mechanical efficiencies are received as physical signals at ports EV and EM, respectively.

• In the Input signal - volumetric and mechanical loss parameterization, the leakage flow rate and friction torque are received as physical signals at ports LV and LM, respectively.

Nominal displacement — Fixed-volume fluid displacement

30 cm^3/rev (default) | scalar

Amount of fluid displaced by shaft rotating under nominal operating conditions.

Dependencies

To enable this parameter, set Leakage and friction parameterization to Analytical.

Nominal shaft angular velocity — Shaft angular velocity

1800 rpm (default) | scalar

Angular velocity of the shaft under nominal operating conditions.

Dependencies

To enable this parameter, set Leakage and friction parameterization to Analytical.

Nominal pressure gain — Pressure gain between fluid entry and exit

10 MPa (default) | scalar

Pump pressure gain between the fluid entry and exit under nominal operating conditions.

Dependencies

To enable this parameter, set Leakage and friction parameterization to Analytical.

Volumetric efficiency at nominal conditions — Ratio of actual flow rate to ideal flow rate

0.92 (default) | positive scalar in the range of (0,1]

Ratio of actual flow rate to ideal flow rate at nominal conditions.

Dependencies

To enable this parameter, set Leakage and friction parameterization to Analytical.

No-load torque — Baseline torque

0 N*m (default) | scalar

Minimum value of torque to overcome seal friction and induce shaft motion.

Dependencies

To enable this parameter, set Leakage and friction parameterization to Analytical.

Mechanical efficiency at nominal conditions — Ratio of actual to ideal mechanical power

0.88 (default) | positive scalar

Ratio of actual mechanical power to ideal mechanical power at nominal conditions.

Dependencies

To enable this parameter, set Leakage and friction parameterization to Analytical.

Pressure gain vector, dp — Vector of pressure data for tabulated data parameterization

[.1, 1, 2] MPa (default) | 1-by-n vector

Vector of pressure differential values for the tabular parameterization of leakage and torque friction. This vector forms an independent axis with the Shaft angular velocity vector, w and the Displacement vector, D parameters for the 3-D dependent Volumetric efficiency table, e_v(dp,w,D) and Mechanical efficiency table, e_m(dp,w,D) parameters. The vector elements must be listed in ascending order.

Dependencies

To enable this parameter, set Leakage and friction parameterization to either:

• Tabulated data - volumetric and mechanical efficiencies

• Tabulated data - volumetric and mechanical losses

Shaft angular velocity vector, w — Vector of angular velocity data for tabulated data parameterization

[250, 500, 1000, 2000, 3000, 4000] rpm (default) | 1-by-n vector

Vector of angular velocity data for the tabular parameterization of leakage and torque friction. This vector forms an independent axis with the Pressure gain vector, dp and the Displacement vector, D parameters for the 3-D dependent Volumetric efficiency table, e_v(dp,w,D) and Mechanical efficiency table, e_m(dp,w,D) parameters. The vector elements must be listed in ascending order.

Dependencies

To enable this parameter, set Leakage and friction parameterization to either:

• Tabulated data - volumetric and mechanical efficiencies

• Tabulated data - volumetric and mechanical losses

Displacement vector, D — Vector of displacement volumes for tabulated data parameterization

[-30, -19, 19, 30] cm^3/s (default) | 1-by-n vector

Vector of fluid volumetric displacement data for the tabular parameterization of leakage and torque friction. This vector forms an independent axis with the Shaft angular velocity vector, w and the Pressure gain vector, dp parameters for the 3-D dependent Volumetric efficiency table, e_v(dp,w,D) and Mechanical efficiency table, e_m(dp,w,D) parameters. The vector elements must be listed in ascending order.

Dependencies

To enable this parameter, set Leakage and friction parameterization to either:

• Tabulated data - volumetric and mechanical efficiencies

• Tabulated data - volumetric and mechanical losses

Volumetric efficiency table, e_v(dp,w,D) — Volumetric efficiency for tabulated data parameterization

repmat([.816, .908, .954, .977, .981, .984; .325, .663, .831, .916, .925, .946; .137, .568, .78, .892, .893, .91], 1, 1, 4) (default) | M-by-N-by-P matrix

M-by-N-by-P matrix of volumetric efficiencies at the specified fluid pressure gain, shaft angular velocity, and volumetric displacement. Linear interpolation is employed between table elements. M, N, and P are the sizes of the corresponding vectors:

• M is the number of vector elements in the Pressure gain vector, dp parameter.

• N is the number of vector elements in the Shaft angular velocity vector, w parameter.

• P is the number of vector elements in the Displacement vector, D parameter.

Dependencies

To enable this parameter, set Leakage and friction parameterization to Tabulated data - volumetric and mechanical efficiencies.

Mechanical efficiency table, e_m(dp,w,D) — Mechanical efficiency for tabulated data parameterization

repmat([.996, .996, .996, .996, .996, .996; .988, .989, .989, .989, .989, .99; .981, .981, .982, .982, .983, .984], 1, 1, 4) (default) | M-by-N-by-P matrix

M-by-N-by-P matrix of mechanical efficiencies at the specified fluid pressure gain, shaft angular velocity, and displacement. Linear interpolation is employed between table elements. M, N, and P are the sizes of the corresponding vectors:

• M is the number of vector elements in the Pressure gain vector, dp parameter.

• N is the number of vector elements in the Shaft angular velocity vector, w parameter.

• P is the number of vector elements in the Displacement vector, D parameter.

Dependencies

To enable this parameter, set Leakage and friction parameterization to Tabulated data - volumetric and mechanical efficiencies.

Volumetric loss table, q_loss(dp,w,D) — Volumetric losses for tabulated data parameterization

repmat([.023, .023, .023, .023, .0285, .032; .0844, .0842, .0845, .084, .1125, .108; .1079, .108, .11, .108, .1605, .18] * 1e-3, 1, 1, 4)m^3/s (default) | numerical array

M-by-N-by-P matrix of volumetric leakage at the specified fluid pressure gain, shaft angular velocity, and displacement. Linear interpolation is employed between table elements. M, N, and P are the sizes of the corresponding vectors:

• M is the number of vector elements in the Pressure gain vector, dp parameter.

• N is the number of vector elements in the Shaft angular velocity vector, w parameter.

• P is the number of vector elements in the Displacement vector, D parameter.

Dependencies

To enable this parameter, set Leakage and friction parameterization to Tabulated data - volumetric and mechanical loss.

Mechanical loss table, torque_loss(dp,w,D) — Mechanical losses for tabulated data parameterization

repmat([.002, .002, .002, .002, .002, .002; .0607, .0556, .0556, .0556, .0556, .0505; .1937, .1937, .1833, .1833, .1729, .1626], 1, 1, 4) N*m (default) | numerical array

M-by-N-by-P matrix of friction torque at the specified fluid pressure gain, shaft angular velocity, and displacement. Linear interpolation is employed between table elements. M, N, and P are the sizes of the corresponding vectors:

• M is the number of vector elements in the Pressure gain vector, dp parameter.

• N is the number of vector elements in the Shaft angular velocity vector, w parameter.

• P is the number of vector elements in the Displacement vector, D parameter.

Dependencies

To enable this parameter, set Leakage and friction parameterization to Tabulated data - volumetric and mechanical loss.

Minimum volumetric efficiency — Minimum value of volumetric efficiency

1e-3 (default) | positive scalar in the range of (0,1]

Minimum value of volumetric efficiency. If the input signal is below this value, the volumetric efficiency is set to the minimum volumetric efficiency.

Dependencies

To enable this parameter, set Leakage and friction parameterization to Input signal - volumetric and mechanical efficiencies.

Maximum volumetric efficiency — Maximum value of volumetric efficiency

1 (default) | positive scalar in the range of (0,1]

Maximum value of volumetric efficiency. If the input signal is above this value, the volumetric efficiency is set to the maximum volumetric efficiency.

Dependencies

To enable this parameter, set Leakage and friction parameterization to Input signal - volumetric and mechanical efficiencies.

Minimum mechanical efficiency — Minimum value of mechanical efficiency

1e-3 (default) | positive scalar in the range of (0,1]

Minimum value of mechanical efficiency. If the input signal is below this value, the mechanical efficiency is set to the minimum mechanical efficiency.

Dependencies

To enable this parameter, set Leakage and friction parameterization to Input signal - volumetric and mechanical efficiencies.

Maximum mechanical efficiency — Maximum value of mechanical efficiency

1 (default) | positive scalar in the range of (0,1]

Maximum value of mechanical efficiency. If the input signal is above this value, the mechanical efficiency is set to the maximum mechanical efficiency.

Dependencies

To enable this parameter, set Leakage and friction parameterization to Input signal - volumetric and mechanical efficiencies.

Pressure gain threshold for pump-motor transition — Pressure threshold for mode transition

1e-3 MPa (default) | positive scalar

Threshold pressure gain value for the transition between pump and motor functionality. A transition region is defined around 0 MPa between the positive and negative values of the pressure gain threshold. Within this transition region, the computed leakage flow rate and friction torque are adjusted according to the transition term α to ensure smooth transition from one mode to the other.

Dependencies

To enable this parameter, set Leakage and friction parameterization to either:

• Tabulated data - volumetric and mechanical efficiencies

• Input signal - volumetric and mechanical efficiencies

• Input signal - volumetric and mechanical losses

Angular velocity threshold for pump-motor transition — Angular velocity threshold for mode transition

100 rpm (default) | positive scalar

Threshold angular velocity value for the transition between motor and pump functionality. A transition region is defined around 0 rpm between the positive and negative values of the angular velocity threshold. Within this transition region, the computed leakage flow rate and friction torque are adjusted according to the transition term α to ensure smooth transition from one mode to the other.

Dependencies

To enable this parameter, set Leakage and friction parameterization to:

• Tabulated data - volumetric and mechanical efficiencies

• Input signal - volumetric and mechanical efficiencies

• Input signal - volumetric and mechanical loss

Check if operating beyond the range of supplied tabulated data — Whether to notify if extents of supplied data are surpassed

None (default) | Warning | Error

Whether to notify if the extents of the supplied data are surpassed. Select Warning to be notified when the block uses values beyond the supplied data range. Select Error to stop the simulation when the block uses values beyond the supplied data range.

Dependencies

To enable this parameter, set Leakage and friction parameterization to:

• Tabulated data - volumetric and mechanical efficiencies

• Tabulated data - volumetric and mechanical losses

Check if operating beyond pump mode — Whether to notify if block operates outside of the pump mode functionality

None (default) | Warning | Error

Whether to notify if block operates outside of the pump mode functionality. Select Warning to be notified when the block operates in the forward or reverse motor modes. Select Error to stop the simulation when the block operates in the forward or reverse motor modes.

Dependencies

To enable this parameter, set Leakage and friction parameterization to Input signal - volumetric and mechanical losses.

Check if pressures are less than pump minimum pressure — Whether to notify if fluid exit pressure is low

None (default) | Warning | Error

Whether to notify if the fluid at port A or B experiences low pressure. Select Warning to be notified when the outlet pressure falls below a minimum specified value. Select Error to stop the simulation when the outlet pressure falls below a minimum specified value.

The parameter helps to identify potential conditions for cavitation, when the fluid pressure falls below the fluid vapor pressure.

Pump minimum pressure — Lower threshold of acceptable pressure at the pump outlet

0.101325 MPa (default) | positive scalar

Lower threshold of acceptable pressure at the pump inlet or outlet.

Dependencies

To enable this parameter, set Check if pressures are less than pump minimum pressure to:

• Warning

• Error

Pressure Compensation

Maximum displacement — Upper limit to pump displacement

30 cm^3/rev (default) | scalar

Upper limit to pump displacement.

Minimum displacement — Lower limit to pump displacement

0.1 cm^3/rev (default) | scalar

Lower limit to pump displacement.

Set pressure differential — Threshold value for variable-displacement functionality

10 MPa (default) | positive scalar

Threshold value beyond which pump displacement is adjusted.

Pressure regulation range — Variable-displacement operational range

0.6 MPa (default) | positive scalar

Variable-displacement operational range. The pump operates between the Set pressure differential and the pump maximum pressure, which is p_set + p_regulation.

Displacement dynamics — Whether to account for flow response to displacement changes

Off (default) | On

Whether to account for transient effects to the fluid system due to changes in pump fluid displacement. Setting Displacement dynamics to On approximates the condition change by introducing a first-order lag in the flow response. The magnitude of the Time constant also impacts the modeled displacement dynamics.

Time constant — Flow response time constant

0.1 s (default) | positive scalar

Constant that captures the time required for the fluid to reach steady-state when changing the fluid displacement. This parameter impacts the modeled displacement dynamics.

Extended Capabilities

C/C++ Code Generation
Generate C and C++ code using Simulink® Coder™.

Version History

Introduced in R2020a

R2024a: Check if block operates outside range of calculated data

The Check if operating beyond the octants of supplied tabulated data parameter has been renamed to Check if operating beyond the range of supplied tabulated data. You can enable the Check if operating beyond the range of supplied tabulated data parameter to check if the block is operating beyond the data specified in the block parameters, that is, operating in a region where the block has extended the data.