Benchmark Solving a Linear System by Using GPU Coder
This example shows how to benchmark solving a linear system by generating CUDA® code. Use matrix left division, also known as mldivide or the backslash operator (\), to solve the system of linear equations A*x = b for x (that is, compute x = A\b).
Third-Party Prerequisites
Required
This example generates CUDA MEX and has the following third-party requirements.
CUDA enabled NVIDIA® GPU and compatible driver.
Optional
For non-MEX builds such as static, dynamic libraries or executables, this example has the following additional requirements.
NVIDIA toolkit.
Environment variables for the compilers and libraries. For more information, see Third-Party Hardware and Setting Up the Prerequisite Products.
Verify GPU Environment
To verify that the compilers and libraries necessary for running this example are set up correctly, use the coder.checkGpuInstall function.
envCfg = coder.gpuEnvConfig('host');
envCfg.BasicCodegen = 1;
envCfg.Quiet = 1;
coder.checkGpuInstall(envCfg);Determine the Maximum Data Size
Choose the appropriate matrix size for the computations by specifying the amount of system memory in GB available to the CPU and the GPU. The default value is based only on the amount of memory available on the GPU. You can specify a value that is appropriate for your system.
g = gpuDevice; maxMemory = 0.1*g.AvailableMemory/1024^3;
Note:
This example uses cuSOLVER libraries that have significant GPU memory requirements for creating workspaces. If you run into CUDA out-of-memory errors, reduce the maxMemory or the matrix step sizes in sizeSingle and sizeDouble.
The Benchmarking Function
This example benchmarks matrix left division (\) including the cost of transferring data between the CPU and GPU, to get a clear view of the total application time when using GPU Coder™. The application time profiling must not include the time to create sample input data. The getData.m function generates test data separately from the entry-point function that solves the linear system.
type getData.mfunction [A, b] = getData(n, clz)
% Copyright 2017-2022 The MathWorks, Inc.
fprintf('Creating a matrix of size %d-by-%d.\n', n, n);
A = rand(n, n, clz) + 100*eye(n, n, clz);
b = rand(n, 1, clz);
end
The Backslash Entry-Point Function
The backslash.m entry-point function encapsulates the (\) operation for which you want to generate code.
type backslash.mfunction [x] = backslash(A,b)
%#codegen
% Copyright 2017-2022 The MathWorks, Inc.
coder.gpu.kernelfun();
x = A\b;
end
Generate the GPU Code
Create a function to generate the GPU MEX function based on the particular input data size.
type genGpuCode.mfunction [] = genGpuCode(A, b)
% Copyright 2017-2022 The MathWorks, Inc.
cfg = coder.gpuConfig('mex');
evalc('codegen -config cfg -args {A,b} backslash');
end
Choose a Problem Size
The performance of the parallel algorithms that solve a linear system depends greatly on the matrix size. This example compares the performance of the algorithm for different matrix sizes (multiples of 1024).
sizeLimit = inf; if ispc sizeLimit = double(intmax('int32')); end maxSizeSingle = min(floor(sqrt(maxMemory*1024^3/4)),floor(sqrt(sizeLimit/4))); maxSizeDouble = min(floor(sqrt(maxMemory*1024^3/8)),floor(sqrt(sizeLimit/8))); step = 1024; if maxSizeDouble/step >= 10 step = step*floor(maxSizeDouble/(5*step)); end sizeSingle = 1024:step:maxSizeSingle; sizeDouble = 1024:step:maxSizeDouble; numReps = 5;
Compare Performance: Speedup
Use the total elapsed time as a measure of performance because that enables you to compare the performance of the algorithm for different matrix sizes. Given a matrix size, the benchmarking function creates the matrix A and the right-side b once, and then solves A\b a few times to get an accurate measure of the time it takes.
type benchFcnMat.mfunction time = benchFcnMat(A, b, reps)
% Copyright 2017-2022 The MathWorks, Inc.
time = inf;
% Solve the linear system a few times and take the best run
for itr = 1:reps
tic;
matX = backslash(A, b);
tcurr = toc;
time = min(tcurr, time);
end
end
Create a different function for GPU code execution that invokes the generated GPU MEX function.
type benchFcnepu.mfunction time = benchFcnGpu(A, b, reps)
% Copyright 2017-2022 The MathWorks, Inc.
time = inf;
gpuX = backslash_mex(A, b);
for itr = 1:reps
tic;
gpuX = backslash_mex(A, b);
tcurr = toc;
time = min(tcurr, time);
end
end
Execute the Benchmarks
When you execute the benchmarks, the computations can take a long time to complete. Print some intermediate status information as you complete the benchmarking for each matrix size. Encapsulate the loop over all the matrix sizes in a function to benchmark single- and double-precision computations.
Actual execution times can vary across different hardware configurations. This benchmarking was done by using MATLAB R2022a on a machine with a 6 core, 3.5GHz Intel® Xeon® CPU and an NVIDIA TITAN Xp GPU.
type executeBenchmarks.mfunction [timeCPU, timeGPU] = executeBenchmarks(clz, sizes, reps)
% Copyright 2017-2022 The MathWorks, Inc.
fprintf(['Starting benchmarks with %d different %s-precision ' ...
'matrices of sizes\nranging from %d-by-%d to %d-by-%d.\n'], ...
length(sizes), clz, sizes(1), sizes(1), sizes(end), ...
sizes(end));
timeGPU = zeros(size(sizes));
timeCPU = zeros(size(sizes));
for i = 1:length(sizes)
n = sizes(i);
fprintf('Size : %d\n', n);
[A, b] = getData(n, clz);
genGpuCode(A, b);
timeCPU(i) = benchFcnMat(A, b, reps);
fprintf('Time on CPU: %f sec\n', timeCPU(i));
timeGPU(i) = benchFcnGpu(A, b, reps);
fprintf('Time on GPU: %f sec\n', timeGPU(i));
fprintf('\n');
end
end
Execute the benchmarks in single and double precision.
[cpu, gpu] = executeBenchmarks('single', sizeSingle, numReps);Starting benchmarks with 8 different single-precision matrices of sizes ranging from 1024-by-1024 to 22528-by-22528. Size : 1024 Creating a matrix of size 1024-by-1024. Time on CPU: 0.011866 sec Time on GPU: 0.004042 sec Size : 4096 Creating a matrix of size 4096-by-4096. Time on CPU: 0.246468 sec Time on GPU: 0.023765 sec Size : 7168 Creating a matrix of size 7168-by-7168. Time on CPU: 0.897369 sec Time on GPU: 0.064114 sec Size : 10240 Creating a matrix of size 10240-by-10240. Time on CPU: 2.199820 sec Time on GPU: 0.138756 sec Size : 13312 Creating a matrix of size 13312-by-13312. Time on CPU: 4.589138 sec Time on GPU: 0.253298 sec Size : 16384 Creating a matrix of size 16384-by-16384. Time on CPU: 8.026105 sec Time on GPU: 0.418530 sec Size : 19456 Creating a matrix of size 19456-by-19456. Time on CPU: 12.909238 sec Time on GPU: 0.640920 sec Size : 22528 Creating a matrix of size 22528-by-22528. Time on CPU: 19.308684 sec Time on GPU: 0.935741 sec
results.sizeSingle = sizeSingle;
results.timeSingleCPU = cpu;
results.timeSingleGPU = gpu;
[cpu, gpu] = executeBenchmarks('double', sizeDouble, numReps);Starting benchmarks with 6 different double-precision matrices of sizes ranging from 1024-by-1024 to 16384-by-16384. Size : 1024 Creating a matrix of size 1024-by-1024. Time on CPU: 0.024293 sec Time on GPU: 0.010438 sec Size : 4096 Creating a matrix of size 4096-by-4096. Time on CPU: 0.431786 sec Time on GPU: 0.129416 sec Size : 7168 Creating a matrix of size 7168-by-7168. Time on CPU: 1.684876 sec Time on GPU: 0.559612 sec Size : 10240 Creating a matrix of size 10240-by-10240. Time on CPU: 4.476006 sec Time on GPU: 1.505087 sec Size : 13312 Creating a matrix of size 13312-by-13312. Time on CPU: 8.845687 sec Time on GPU: 3.188244 sec Size : 16384 Creating a matrix of size 16384-by-16384. Time on CPU: 17.680626 sec Time on GPU: 5.831711 sec
results.sizeDouble = sizeDouble; results.timeDoubleCPU = cpu; results.timeDoubleGPU = gpu;
Plot the Performance
Plot the results and compare the performance on the CPU and the GPU for single and double precision.
First, look at the performance of the backslash operator in single precision.
fig = figure; ax = axes('parent', fig); plot(ax, results.sizeSingle, results.timeSingleGPU, '-x', ... results.sizeSingle, results.timeSingleCPU, '-o') grid on; legend('GPU', 'CPU', 'Location', 'NorthWest'); title(ax, 'Single-Precision Performance') ylabel(ax, 'Time (s)'); xlabel(ax, 'Matrix Size');
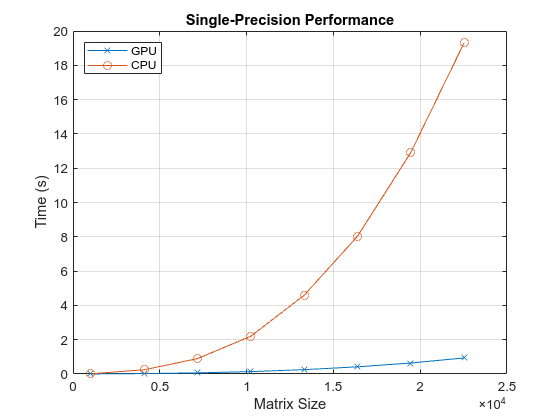
drawnow;
Now, look at the performance of the backslash operator in double precision.
fig = figure; ax = axes('parent', fig); plot(ax, results.sizeDouble, results.timeDoubleGPU, '-x', ... results.sizeDouble, results.timeDoubleCPU, '-o') legend('GPU', 'CPU', 'Location', 'NorthWest'); grid on; title(ax, 'Double-Precision Performance') ylabel(ax, 'Time (s)'); xlabel(ax, 'Matrix Size');
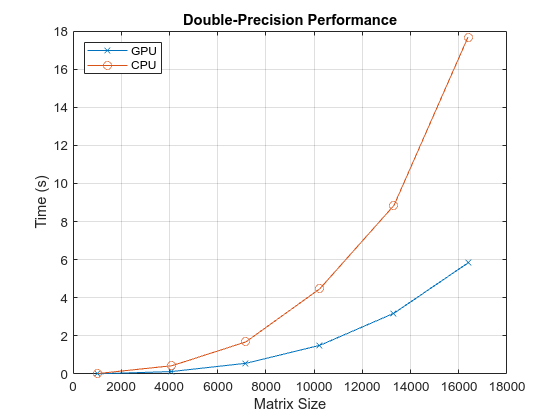
drawnow;
Finally, look at the speedup of the backslash operator when comparing the GPU to the CPU.
speedupDouble = results.timeDoubleCPU./results.timeDoubleGPU; speedupSingle = results.timeSingleCPU./results.timeSingleGPU; fig = figure; ax = axes('parent', fig); plot(ax, results.sizeSingle, speedupSingle, '-v', ... results.sizeDouble, speedupDouble, '-*') grid on; legend('Single-precision', 'Double-precision', 'Location', 'SouthEast'); title(ax, 'Speedup of Computations on GPU Compared to CPU'); ylabel(ax, 'Speedup'); xlabel(ax, 'Matrix Size');

drawnow;
See Also
Functions
codegen|coder.gpu.kernel|coder.gpu.kernelfun|gpucoder.matrixMatrixKernel|coder.gpu.constantMemory|stencilfun|coder.checkGpuInstall